科学が対象とするものは,物質とエネルギーと情報[1]であるといわれる.また,人間社会を物質(もの)と精神(こころ)とに大別し,「こころ」が最も重要であるという論議がある.「こころ」あるいは「感情(感性)」に迫る工学的手法として,感性スペクトラム分析法(
emotion spectrum analysis method)がある.[2] これは,脳波を分析することにより感性マトリクスを求め,感情を数値的に表すものである.情報とは,このような人間の精神活動に直結した「何か」であると考える.シャノンは,「情報とは,それを得ることによってその対象について考えられる種々の可能性が限定され,不確かさが除去されることである」と定義している.
JIS
(Z8121)では,情報量(amount of information)とは「情報のもつ不確実性の度合」であるとし,ある対象iの生起確率をp(i),事象jが生起したという条件のもとでの対象iの実現確率をp(i|j)とするとき,対象iの実現を予言する場合に事象jの生起がもたらす情報量Iは,I = log p (i|j) / p(i) eq. 1.5
と定義している.
例えば,サイコロを3回振って続けて1の目が出る確率p(i),は1/63である.ここで1回目に1が出た(事象j1)あと続けてあとの2回1の目が出る確率p(i|j1)は1/62,はじめの2回続けて1の目が出た(事象j2)あと3回目に1の目が出る確率p(i|j2)は1/6であるから,事象j1,j2の情報量をそれぞれI1,I2とすると
I1 = log p (i|j1) / p(i) = log 6 eq. 1.6
I2 = log p (i|j2) / p(i) = log 62 = 2 log 6 eq. 1.7
すなわち,はじめの2回続けて1が出たという情報量は,1回のみ1が出たという情報量の2倍である.
情報の価値は,起こりうる確率
pが小さいほどそれが起こったことを知ったときの値打ちが大きいことからpの逆数の関数で表されよう.また,情報源(
information source)のもつ平均情報量をエントロピー(entropy)Hとよび,次式で表わす.
H = -∑ pi log2 pi eq.1.8
i=1-n
ここで,p1,p2,…pnは,情報源における各事象の生起確率である.
結果が既知である現象は何が起こるかという確率pが1であるのでエントロピーHは0であるし,滅多に起こらない事象を知る情報のエントロピーは大きい.したがって,情報の価値や量はエントロピーが大きいものを知るほど大きいといえよう.
たとえば,明日雨が降る確率をpとすると,明日雨が降らない確率qは1-pであり,明日雨が降るか降らないかという不確かさのエントロピーHはつぎのように表される.
H=-plog2p-qlog2q
=-plog2p-(1-p)log2(1-p) eq.1.9
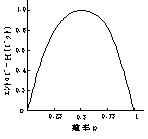
pとHの関係は図1.3のように,p=1または0のときH=0で最小になる.すなわち晴天が続いているとき明日雨が降らないことは確定的でありエントロピーは小さく,降るか降らないか五分五分のときはエントロピーは大きく予測がつけがたいといえる.

図1
.3 明日の天候のエントロピー●ソフトウエア:entro_64.exe
なお,情報量の単位としては,確率
1/2のどちらかが起こることを示すものである1ビット(bit)が用いられる.図1.3で,p=0.5のときのHは1ビットである.情報を得るということは不確かさを減らすということであるから,情報が増加するとエントロピーは減少することになる.
一般に自然現象では情報のエントロピー[3]は増大の方向へ変化する(エントロピー増加の法則)といわれるので,情報活動は自然界の変化に逆らって秩序あるシステムを作り出すことであるといえよう.
生物生産システムの解析,設計,計画には,土壌,気象,作物,経済などの広い分野の情報がなくてはならないものであり,その成果の優劣は情報の多少によって決まるといっても過言ではないであろう.
次へ[1] 大村 平:情報のはなし,日科技連,1970
[2] 武者利光:「こころ」を計る,日経サイエンス,26-4,p20-29,1966
[3] 竹内 訳:エントロピーの法則,祥伝社,1982: ☆apx.161:エントロピー Entropy:B54161.doc