2.2 Origin of geomagnetism
- Motion of charged particles responsible for magnetism -
2.2.1 What is happening with the daily change of geomagnetism ?
-Why does geomagnetism increase by about 0.1% around noon?-
It has been explained that the Earth has geomagnetism,
and because magnetic lines surround the Earth,
the ground of the Earth is protected from the charged particles those come
from the Sun. So, the influence of the solar wind has not been discussed
much. However, the Earth's magnetosphere is significantly different between
the day hemisphere side and the night hemisphere side. The mechanism by
which the magnetosphere deforms is related to the charged particles those
come from the Sun.
As shown in Fig.2.2.1, the intensity of geomagnetism around noon on the
day when the Sun is mild has a periodic increase of about 0.1%. Around
noon, the density of charged particles in the upper sky can be increased
by the irradiation of the sun's X-rays and ultraviolet rays.

Fig. 2.2.1 Geomagnetism Day Change
The ultraviolet rays decompose oxygen and nitrogen molecules in the Earth's
upper atmosphere into free atoms. The atoms are further ionized to electrons
and ions. The charged particles rotate counterclockwise due to the rotation
of the Earth, and a magnetism is generated by the counterclockwise orbit
of the charged particles in the upper sky.
Since the mass of electrons is 1/(1836) that of protons, the movement
of electrons depends on the movement of protons. Here, the charge of electron
is negative, i.e. polar opposite to H+.
Although it cancels each other out, there are a lot of hydrogen ions
(H+) as a whole in the sky above the Earth's upper sky
The number of H+ is larger than that of electron in the thermosphere,
the electric current moves the same direction accompanied with the rotation
of the Earth. So, the geomagnetic magnetic field line on the surface of
the Earth goes from the South Pole to the North Pole as shown in Fig.2.2.2.
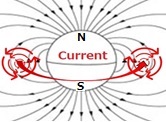
Fig.2.2.2 Magnetism generated by the H+ orbiting the Earth in the sky
As shown in Fig.2.2.3, the mesured values of geomagnetic field are larger
than the value of the magnetic field due to the charged particles. Ther
geomagnetism on the Earth's surface laye is stronger in high latitudes.

Fig.2.2.3 Measured values of geomagnetism on Earth's surface
Fig. 2.2.4 shows the flow of hydrogen ions in the solar wind that affects
the Earth's geomagnetism. Near the equator in the daytime hemisphere, the
solar wind collides with the atmosphere from the front. Due to the angular
momentum of the counterclockwise rotation of the Sun, the atmosphere is
driven the trade wind of clockwise flow. The solar wind drives ions in
the sky above the east side of the Earth's mid-latitudes, where the ions
of the atmosphere moving in the counterclockwise Earth's rotation are coupled
with H+ of the solar wind by the effect of parallel currents.
In the west side, the influence of the solar wind is weak because the ions of the Earth are magnetically repulsed with H+ of the solar wind. As a result, westerlies blow at mid-latitudes

Fig. 2.2.4 Flow of H+ of the solar wind that affects the Earth's geomagnetism.
Thus, a slight increase in geomagnetism at noon can be understood as
the phenomenon that increases the number of electrons in the plasma moving
in the opposite direction to the proton through the magnetic effect that
the energy state of parallel currents is low.
2.2.2 Why magnetic of motion of charged particle must be considered by
vector potential, not magnetic field
-A motion of charged particle generates the vector potential (A)-
Charged particles interact magnetically when they run side by side. According
to the Aharonov-Baume effect, the magnetic interaction between partial
current and charge particle on the move must be considered by vector potential
A, not magnetic field B.
As shown in Fig.2.2.5, the Aharonov-Bohm effect is a phenomenon in which
the material waves of electrons passing up and down outside of the solenoid
are different phases, and interference fringes are observed. In 1986, Akira
Sotomura succeeded in testing this effect in the sample covered with a
superconductor on the solenoid.

Fig. 2.2.5 Aharonov-Bohm Effect that is magnetic phenomenon on the electron
beam through an outside of solenoid coil. This figure is reproduced from
http://dolphin.phys.s.u-tokyo.ac.jp/research/sc2des/ws/ab.html
The magnetic field (B) above and below the solenoid are the same, but the direction of the open
partial current generating the magnetic field is opposite, and the vector
potential (A) that generates the magnetic field around the open partial current is
the opposite direction. Therefore, the motion of electrons moving in the
solenoid coil and electrons passing outside the solenoid interacts, causing
a difference in the phase of electrons passing up and down of the outside
of the solenoid.
2.2.3 Magnetism on open partial current is dealt with vector potential
-Magnetic field line is generated by a rotation of vector potential.-
The magnetic field creates torque tangentially on a plane perpendicular to the direction of the magnetic field. The energy of rotation of the vertical area that changes due to the change in the rotation angle is proportional to the square of the radius,
and the magnetic field line passing through the area also changes at the square of the radius.
The vector potential (A) is defined by Eq.1.
B = rot A (1)
Since the micro rotations offset internally from the Stokes' theorem,
the torque appears only in the outer circumference. The area of the angle of
the magnetic field (B) gives torque, and the value of rotational energy
corresponds to the angle integration of the torque. So, the energy of the
rotational motion on the charge particles at velocity (v)
in the field of vector potential (A) is given by Eq.2.
Um = - (qv)・A (2).
Here, the negative sign is set so that the energy is lower when v and
A are parallel. The change in the angle of energy (Um) of rotational motion
is torque. Therefore, the rotation of Eq.2 becomes torque.
FL = rot Um = - (qv)・rotA (3).
The torque received by the charge particle (q) of velocity v from magnetic
field B is given by Eq. 3, and it is equal to Eq.4 of Biot–Savart law.
FL = - (qv) xB (4)
Eq.3 matches with Eq.4, because the minute angle change in the area of
B is equal to the minute angle change of A. Fig 2.2.6 shows the relationship between vector potential A and magnetic field B.

Fig..2.2. 6 The relationship between vector potential A and magnetic field B
There is Maxwell's of Eq.4 in which the current density(j) plus the displacement current (ε0∂E/∂t) are rot B.
rot B =μ0(j -ε0∂E/∂t) (5).
The value on the angle integral of B is the value on the area integral of the current density.
From Eq.1 and Eq.5, we get Eq.6.
rot (rot A) =μ0(j -ε0∂E/∂t) (6).
Maxwell's equations of ∂B/∂t=rot E becomes Eq. of ∂A/∂t=-E. Therefore, Eq.7 is obtained from Eq.6
. rot (rot A) = μ0(j -ε0∂2A/∂t2) (7).
Eq.10 can be obtained using the Eq.8 and Eq.9 of the gauge transformation.
rot(rotA)=grad(divA) - △A (8)
div (A+ gradΛ) = 0 (9).
△A=(μ0ε0) ∂2A/∂t2 - μ0j (10).
△≡∂2/∂x2+∂2/∂y2+∂2/∂z2.
(ε0)∂2A/∂t2≫- j In case of (ε0)∂2A/∂t2≫- j ,
Eq.10 becomes a wave equation as expressed as Eq.11.
△A=(μ0ε0) ∂2A/∂t2 (11).
(ε0)∂2A/∂t2≪-j In case of (ε0)∂2A/∂t2≪-j, Eq.12 is equivalent to the Poisson equation (△V= -ρ/ε0) that indicates relationship between electric charge density of ρ and
potential V.
△A= - μ0j (12).
In the Poisson equation, the electric fied E of a point charge acts in a three-dimensional direction. On the other
hand, A is in proportional to the product of the velocity and density of the charge
particles according to Eq.12. The direction of A with the energy of rotation accompanies with the current j.
When a charged particle moves, it approaches and leaves, and the value of A changes.
Its partial current (j) changes the energy of rotation, A, over time.
From Eq.∂A/∂t=-E, the electric field of E acts to the other charged particle momentarily.
Although the magnetic attractive force acts at the moment when the charged
particles having the same polarity move side by side, the magnetic repulsion
force acts momentarily in the case of particles with different polarity.
to Index -2.2-