 |
| 図.1 クイックソート |
|---|
今回紹介するソート法はおそらく最も使用頻度の高いソート法になると思います。なぜなら...。
それでは、今回の要点です。
では、いってみましょう。
今回のソート法は平均的に最も速い方法として知られてきたソート法です。今でもソート法の開発は続いており、このソート法よりも速いものも現れてきているそうですが、詳しいことは知らないのでそれらについてはこの講座では触れません。
と、大仰に紹介しましたが、ソート法のアルゴリズム自体は簡単です。
先ず、ある値よりも小さい要素を配列の前半に、大きい要素を配列の後半に集めます。この時、「ある値」はそれよりも大きな値も、小さな値も、必ず存在するような値にします。例えば「両端の要素の平均値」などです。また、等しいときはどちらに含めても構いません。
こうしてできた各組でまたこれと同じことをします。これをずっと続けていけばソートができますね。このソート法をクイックソートと呼びます。
では、次の例を見て下さい。
 |
| 図.1 クイックソート |
|---|
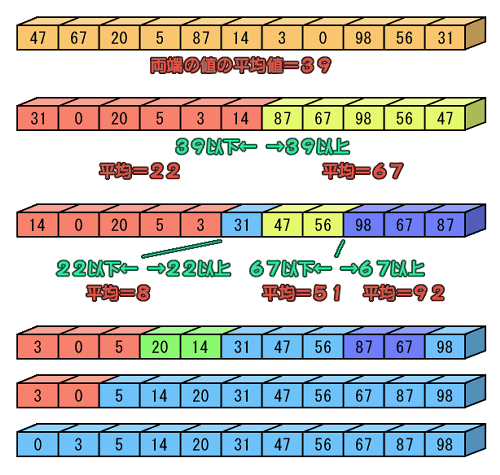
先ず、1番上の配列では、両端要素の平均値は39です。そこで、左からそれ以上の、右からそれ以下の値を探します。そして、その値がでてきたところで両値を交換します。探す位置が交差するまでこれを続ければ、配列を39以下のグループと、39以上のグループに分けることができます。
それを行うと、2番目の配列になります。確認してみて下さい。そして、次に2番目の配列の前半・後半で同じ事をします。そうして3番目の配列ができます。
すると、「31」という要素は1つだけになったので、このブロックはこれでソート終了です。このようにして全ブロックがソートできない状態になったとき(要素が1つだけになったとき)、ソートが終了します。
「各組でまたこれと同じことをします」というのを見て分かるとおり、クイックソート関数は再帰関数にすると便利です。
では、実際に作ってみましょう。
| プログラム |
|---|
// Sort5.cpp
#include "SortData.h"
#include "SortSub.h"
// 再帰関数
static void Sub_QuickSort(int* pnData, int nFirst, int nLast);
// クイックソート
void QuickSort(int* pnData, int nNumOf)
{
Sub_QuickSort(pnData, 0, nNumOf - 1);
}
// 再帰関数
// nFirst : ブロックの最初のインデックス
// nLast : ブロックの最後のインデックス
static void Sub_QuickSort(int* pnData, int nFirst, int nLast)
{
int iLess = nFirst; // 前半のインデックス
int iGreater = nLast; // 後半のインデックス
int x; // 「ある値」
// 「ある値」は両端の要素の平均値にする
x = (pnData[nFirst] + pnData[nLast]) / 2;
// 交換ループ
// 位置が逆になると終了
while(iLess < iGreater)
{
// x より小さい要素は無視
while(pnData[iLess] < x)
iLess++;
// x より大きい要素は無視
while(pnData[iGreater] > x)
iGreater--;
// 位置がちゃんとしているときは交換し、
// iLess と iGreater を1つずつ進める
if(iLess < iGreater)
Swap(pnData[iLess++], pnData[iGreater--]);
}
// iLess == iGreater で終わった時は、
// iGreater < iLess になるようにする
if(iLess == iGreater)
{
if(pnData[iLess] < x)
iLess++;
else if(pnData[iLess] > x)
iGreater--;
}
// 次のブロックのサイズが2以上の時は再帰
if(iLess >= nFirst + 2)
Sub_QuickSort(pnData, nFirst, iLess - 1);
if(iGreater <= nLast - 2)
Sub_QuickSort(pnData, iGreater + 1, nLast);
}
int main()
{
QuickSort(g_anData, g_nNumOf);
DispArray(g_anData, g_nNumOf);
return 0;
} |
| 実行結果 |
1, 1, 4, 6, 9, 9, 10, 11, 13, 14, 15, 16, 23, 25, 28, 29, 31, 33, 34, 39, 39, 40, 40, 41, 42, 44, 48, 51, 51, 53, 54, 55, 56, 63, 67, 68, 73, 73, 76, 77, 78, 79, 79, 87, 89, 99, 99, 101, 101, 103, 110, 112, 116, 117, 117, 118, 124, 128, 136, 137, 137, 138, 148, 150, 152, 155, 157, 160, 161, 164, 166, 167, 168, 169, 173, 173, 174, 175, 185, 186, 188, 192, 199, 203, 213, 215, 222, 228, 228, 229, 231, 235, 239, 240, 240, 242, 249, 249, 254, 255, |
はい、きちんとソートできました。
しかし、やっぱりこれだけではどれだけ速くなったのか分かりませんね。そこで、前回と同じ乱数列をソートしてみたところ、0.3秒程度しかかかりませんでした。少ない要素の配列をソートさせても結構速くソートできます。
ただ、配列によって速度にムラがあるそうです。それでもクイックソートは平均的に高速で、愛用されています。
で、愛用されているということは標準関数が用意されていてもいいですね。それが qsort 関数です。ヘッダファイルは stdlib.h です。
関数のプロトタイプは次の通りです。
void qsort(void* pBase, size_t nNumOf, size_t nElemSize,
int (*fpCompare)(const void* pElem1, const void* pElem2));
第1引数には配列を、第2引数には要素数を、第3引数には1要素のサイズを渡します。
そして、問題は第4引数です。これは関数ポインタですね。つまり、ここには関数を渡すわけです。何の関数かというと、比較関数です。
比較するといってもいろいろな方法があります。例えば構造体のソートなどを考えると、ただ全体を大小比較するだけでは困りますね。ポインタのソートなどは、参照先の大小を比較することでソートするのが普通です。また、昇順だけでなく、降順でソートしたいときもあるでしょう。
そこで、要素をどう比較するかを関数にして、第4引数に渡すのです。
比較関数の型は int (*)(const void* pElem1, const void* pElem2) となっています。例えば、
// int 型要素を昇順ソートするときの比較関数
int IntCompareA(const void* pElem1, const void* pElem2)
{
return *(const int*)pElem1 - *(const int*)pElem2;
}
の Compare を渡すわけです。
引数は、比較する要素のアドレスになります。どんな型の要素でも受け取れるように、こういう仕組みになっています。
で、戻り値の意味は以下の通りです。
| 戻り値 | 意味 |
|---|---|
| 負 | pElem1 の指す要素が pElem2 の指す要素より小さい |
| 0 | pElem1 の指す要素と pElem2 の指す要素は等しい |
| 正 | pElem1 の指す要素が pElem2 の指す要素より大きい |
qsort では、この比較関数の結果を使って昇順でソートを行います。降順でソートしたければ、上の「小さい」と「大きい」の部分を逆に考えればいいです。
// int 型要素を降順ソートするときの比較関数
int IntCompareD(const void* pElem1, const void* pElem2)
{
return *(const int*)pElem2 - *(const int*)pElem1;
}
では、実際にいつもの配列をソートしてみましょう。
| プログラム |
|---|
// Sort6.cpp
#include <stdlib.h>
#include "SortData.h"
#include "SortSub.h"
// int 型要素を昇順ソートするときの比較関数
int IntCompareA(const void* pElem1, const void* pElem2)
{
return *(const int*)pElem1 - *(const int*)pElem2;
}
int main()
{
qsort(g_anData, g_nNumOf, sizeof *g_anData, IntCompareA);
DispArray(g_anData, g_nNumOf);
return 0;
} |
| 実行結果 |
1, 1, 4, 6, 9, 9, 10, 11, 13, 14, 15, 16, 23, 25, 28, 29, 31, 33, 34, 39, 39, 40, 40, 41, 42, 44, 48, 51, 51, 53, 54, 55, 56, 63, 67, 68, 73, 73, 76, 77, 78, 79, 79, 87, 89, 99, 99, 101, 101, 103, 110, 112, 116, 117, 117, 118, 124, 128, 136, 137, 137, 138, 148, 150, 152, 155, 157, 160, 161, 164, 166, 167, 168, 169, 173, 173, 174, 175, 185, 186, 188, 192, 199, 203, 213, 215, 222, 228, 228, 229, 231, 235, 239, 240, 240, 242, 249, 249, 254, 255, |
はい、きちんとソートできましたね。
このように、ソートするときは qsort という関数が用意されているので、バグを避けるためにも、この関数を使うことを奨めます。「今までやってきたのは何だったんだ!」という感じですが、まぁ、いろいろなアルゴリズムを知るのもいいことですよ(汗)。
そして、速いこともさることながら、このことからもクイックソートが最も使用頻度の高いソート法になるでしょう。
では、今回の要点です。
次回も、まだソートをやります。ただ、新しいソート法を出すのではなく、ソートの利用方法についての話です。
Last update was done on 2003.5.4
この講座の著作権はロベールが保有しています