座標に依存する物理量と力　

（2014年8月31日）

（国際宇宙ステーション)
国際宇宙ステーション（ISS)は地球の表面から高度約400Kmの空間を秒速約8Kmで回っています。このISSに乗り込むには、スペース・シャトルが退役した現在、ロシアのソユーズロケットで宇宙に打ち上げられ、ISSとドッキングする必要があります。

このようにして乗り込んだ宇宙飛行士は位置エネルギーも運動エネルギーも大きな量を保持していると考えられます。しかし、宇宙ステーションの中で活動する宇宙飛行士は宇宙ステーションの中では無重力状態になってステーションの中では地上と変わらない動きでしかありません。
秒速８Kmというのは地上に固定した座標に対しての速さであり、高度400Kmも地上に固定した座標で見ての数字です。ところが、宇宙ステーションに原点を固定した座標で見ると速度はゼロであり、高度もゼロです。

物理学では質量×速度の量を運動量といいます。運動エネルギーは1/2×質量×速度＾2です。宇宙飛行士の質量が60Kgあるとしても、宇宙ステーションの中では運動量も運動エネルギーも、速度がゼロなのですから、その量はゼロでしかありません。

秒速8Kmというのは地上の座標での値で、宇宙ステーションに固定した座標では秒速ゼロなのです。つまり、運動量も運動エネルギーも座標に依存した物理量だということです。

（運動量について）
座標に依存する運動量とはどういうものかもう少し考えて見ます。秒速８Kmで運動している宇宙飛行士は、自分が宇宙ステーション内にいる間は窓から外を見ない限り、自分が飛んでいることすら自覚することができません。高速で飛んでいたことが判るのは地球に帰還するに際して、カプセルが大気に突入した時です。カプセルが大気との摩擦で真っ赤になったり、大きな減速度を感じたりして秒速8Kmが途轍もない速度であったことを実感します。

物体の質量がmでこの物体が速度vで飛んでいるとき、この物体は他に何も力が働かなければニュートンの運動の第一法則（慣性の法則）で何時までもvの速度で飛び続けます。この物体の運動量はmvで表します。同じ速度vで飛んでいる間は数値としてmvの量があると考えることはできますが、これは概念上のもので実証することは出来ません。外部から力Fをt秒間加えて速度がゼロになったとき始めて運動量mvはFtの量であったと判るのです。力積Ftは運動量mvの変化量に等しいのです。F=d（mv）／dtがニュートンが表した運動の第2法則の元の形です。

運動エネルギーについても全く同じことが言えます。運動をしていると判定する座標に対して運動を止めるに必要なエネルギー（仕事）を与えて（取り去って）始めて運動エネルギーの量が判るのです。

（力の定義式）
それではニュートンの運動の第2法則で定義された力は座標に依存するのでしょうか。力は質量に加速度を乗じた量であると定義されています。このように定義された力は座標に依存するのでしょうか。加速度は速度を時間で微分した量ですから当然加速度も座標に依存します。質量は座標に依存しなくとも、加速度が座標に依存しますから、力も座標に依存することになります。

力が座標に依存することになると、これは少し困ったことになるのです。

今質量mのペイロードがロケットに乗せられて推力飛行を続けている状況を考えます。ロケットの推力は機体全体を加速させますからペイロードも機体と同じ量だけ加速されます。ペイロードを加速させるのはペイロードを取り付けた機体の場所からですが、ペイロードに加わる力がFで加速度がαだとするとF=mαの関係があります。地上からロケットを見るとペイロードも加速度αで運動していることを観察できますから、ペイロードにはFの力が掛かっていると判ります。しかし、ロケットに固定した座標でみると搭載されたペイロードに相対的な動きはありませんから加速度ゼロで、力が掛かっていないことになります。

実際にはペイロードには力Fが掛かって慣性力mαと釣り合っていることは動かしがたい事実です。ペイロードの構造が弱ければ力Fで壊れてしまうこともあるでしょう。従って、力が座標に依存する定義は適切でなかったと言わざるを得ません。

　それではどうすれば良いのでしょうか。

（力と応力・歪）
　物体の運動を解析するための質点系力学に限れば、力の掛かる物体を一つの点に集中していると想定しますから、現在の力の定義でも全く問題はありません。それは当然です。物体を一つの点に集中させてしまうと応力・歪の概念は無くなってしまうのですから力も点で釣り合わせることが出来るのです。

　質点系力学は、運動解析には非常に便利で、天体の運動や人工衛星、ロケットの軌道解析にも十分役立っていて何も不都合はありません。しかし、点で釣り合うことが出来る力とは大胆な力の簡略化であることには違いありません。材料力学や構造強度解析の分野で使う力の概念とはかけ離れています。質点系力学では力をベクトルとして扱うことができますが、材料力学。構造力学ではもはや力をベクトルとはみなせないのです。

　それでは力とはどのようなものか考えて見ましょう。

（力の釣り合い）
　昔の格言に「暖簾に腕押し、糠に釘」というものがありますが、これは力が入らない状況を示しています。力は釣り合っている状態で始めて認識できるのです。

　今、ここに2本の千枚通し（錐、アイスピックでも構いませんが）を想定してください。2本の千枚通しは理想的に先端をとがらしてあるとします。この二つの千枚通しの先端同志を突き合わせて力を伝えることが出来るでしょうか。

図-１　千枚通し

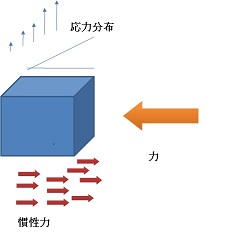
　理想的な千枚通しの先端は鉄の原子が1個です。その後ろは3個の原子が控えていることでしょう。実際にはこのように尖らした千枚通しの先端同志を突き合わせることも至難の技かも知れませんが、思考実験としては十分可能です。しかし、すこし力を入れたら千枚通しの先端は持ちこたえられないでしょう。つまり、点では力を伝えられないのです。同様に、包丁同志の刃を合せて力を伝えることもできません。

　物体に力を及ぼすには面で押し付けることが必要です。するとその物体は動き出します。力を与え続けるとどんどん早く動きます。つまり、物体に力を与えると加速度を持って動き出します。力を与えるのは面ですから2次元です。これに対して質量と加速度を乗じた量が慣性力です。慣性力は物体全体で外から加えた力と釣り合いますから3次元的に発生します。そして、物体内部には応力・歪が発生します。力は慣性力と釣り合うのです。これが力の基本です。

図-2　力と慣性力の釣り合い

　物体は外から加えた力によって加速運動を始めますが、必ずその物体内に応力・歪を発生します。この応力・歪は座標の取り方に依存しません。従って、力の定義を応力・歪を使って定義すれば座標によらなかったわけです。力と応力・歪の関係はフックの法則です。材料によって比例定数が違いますが、材料を決めると単位面積当たりの力（つまり応力）は物体の単位長さあたりの変形量（歪）に比例します。これがフックの法則です。比例定数はヤング率と呼ばれていて、その値は材料によって異なります。

　フックの法則から定義した力であれば座標に依存することはありません。力の定義をニュートンの運動方程式から決めた現状のままとするか、フックの法則から定義し直すかは、今後の検討課題でしょう。

（重力は力か）
　もう一度国際宇宙ステーション（ISS )に戻りましょう。高度400Kmの空間は地球の表面の重力の89％の重力が作用しています。ISSは常に地球に向かって落ちている（自由落下）のですが、水平方向に秒速約８Kmの速度がありますので、何時までも地表に辿り着かないのです。このことはニュートンが最初に指摘したとおりです。

一方、ISSは無重力状態になっています。重力が力であると考えるニュートン力学では、ISS が無重力状態にあるのは遠心力（慣性力）と釣り合っているからであると説明します。力の釣り合いであるならば、応力・歪が発生する筈です。ところが、応力・歪は全く検知できません。果たして、力の釣り合いと言えるのでしょうか。

ニュートン力学では、ISSが無重力状態になっているのはISSを構成する物体の全ての分子が分子単位で重力と慣性力が釣り合っているから、応力・歪の発生がないのであると説明するしかありません。

（アインシュタインの発見）
　アインシュタインは思考実験の結果、重力により自由落下する物体には重力が消えていることに気が付きました。アインシュタインはこの事実を生涯最高の思いつきであって1907年のことだったと、後に世界各地での講演で語っています。

　等速直線運動している物体も、物体に固定した座標でみればその物体の運動量がゼロでした。運動を止めた時に始めて運動量がどの程度であったか判るのでした。

　重力の場合も同じです。運動を止めた時に始めて力として感知できるのです。これはN（ニュートン）を単位とする重さ、または重量です。地上においた物体は地面で加速度運動が止められていますから、全ての物体には重さがあるように錯覚するのです。全ての物体にあるのは重さでなく質量です。

　従って、重力の作用は、その加速度運動を止めたときに力（慣性力）として（3次元で）現れますが、通常は加速度運動を生じさせる作用なのです。これが「重力は加速度」の意味です。

　重力による物体の加速度運動（自由落下）は外から見れば加速度運動であると判るのですが、物体に固定した座標では当然のことながら加速度もゼロです。現在の力の定義にしたがえば、自動的に力もゼロということになります。

　アインシュタインは力の定義から自由落下で重力が消えていると気が付いたのではありません。重力の全く作用しないどの星からも遠く離れた宇宙空間にいる物体の状態と、物体が自由落下状態にあるのと同じであると気が付いたのです。分子単位で力が釣り合っていると考えてもそれを実証することはできません。力が何も作用していないのと区別がつかないならば同じとしなければならないということです。論理的に違いが無いのを同じ認めようというのが等価原理です。この等価原理から自由落下状態にある物体には重力が消えていると気が付いたのです。

(了）

戻る