|
(2016年8月21日)
(質量とは)
あらゆる物質や物体が普遍的に持つ唯一の特性が質量(mass)です。質量を持たないものとして光子がありますが光子は物体でも物質でもありません。同じ物質で出来ている物体なら大きなものほど質量は大きいのです。同じ大きさの鉄のボールと木のボールなら鉄のボールの方が質量は大きいのです。概して、大きくて密度の高い物体は質量が大きいのです。質量の単位は[㎏]です。
質量と重さは、しばしば混同して用いられていますが明確に違います。地上では質量のある物体は重さがあります。では重さとは何でしょうか。
地上にあるすべての物体は重力によって落下する性質があります。この落下を止めようとするときに働く慣性力が重さなのです。
重さは力です。1㎏の質量の物体は地上では1[㎏重](工学単位)または9.8[N]の重さがあります。地球の軌道を回っている宇宙ステーションの中では質量1㎏の物体も重さは0[N]です。
さて、質量は㎏という単位を使って大きさを表しますが、質量の定義はどうなのでしょうか。
質量が大きいということは動かしにくいということです。もう少し正確な言い方をするならば、質量が大きいほど運動状態に変化を起こしにくいということです。止まっているものを動かしたり、動いているものを止めたりさらに早く動かしたりすることが運動状態の変化です。
運動状態の変化は速度を変化させることですから、加速または減速させるということです。物体の運動状態を変化させる、つまり加・減速させるためには力の作用が必要です。
質量mの物体に力Fを作用させるとその物体は加速度αで運動状態が変化するとき、F=mαの関係があります。この式がニュートンの運動方程式と呼ばれる関係式です。この式から質量の単位を決めることが一番自然な決め方だと思われます。
(新しい質量の定義)
次のように決めるのが良さそうです。
「1単位の質量とは、1単位の力を与えたとき1単位の加速度を生じる大きさとする。」
現在のMKS単位系では加速度の単位は[m/s^2]です。力の単位はニュートンの功績を称えて[N]となっています。そして質量の単位は[㎏]です。すると質量の単位の次元は次のようになります。
[㎏]=[N/(m/s^2)]=[N・s^2/m]
実際にこの定義式から、ある物体の質量を測定するために既知の力を与えてその物体が得た加速度を測定するということは非常に困難でしょうし、精度が期待できません。実際の質量測定はいままでどうりの方法に寄らざるを得ないでしょう。また質量は基本単位の一つですから合成単位とすべきではないという意見もあるでしょう。しかし、物理的な意味から質量を定義すると上述のようにすべきと思われるのです。何を基本単位に選ぶかは選択の問題ですから。
もちろん、現在のところ、質量は合成単位ではありません。動かしにくさという物理的な意味を離れて、単に㎏原器の質量を1㎏と定め、基本単位としています。
(力の定義)
それでは1単位の力とは現在どのように定義されているのかを見ましょう。力とは質量のある物体に加速度を与える作用であるとされています。そして、ニュートンの運動方程式から、「1単位の力とは1単位の質量に1単位の加速度を与える作用である」としています。
力の単位の次元は次のようになっています。
[N]=[㎏・m/s^2]
ここで、ニュートンの運動方程式を力の定義のために使っているので質量の単位にニュートンの運動方程式を使えなくなったのかも知れません。
(新しい力の定義)
ニュートンの運動方程式は質量の定義に使うものとして、力の定義には他の式が使えないものででしょうか。ここで、物体に力が作用したときにその物体は運動の変化をもたらすだけでしょうか。実はもう一つ変化があります。それは物体内部に応力が発生しひずみが生じるという現象です。
物体に力が作用したとき、その物体の①運動状態が変化するということと、その物体には②応力・ひずみが生じるという二つの現象がありますが、果たしてどちらが本質的なのでしょうか。
今長方体の形状をした質量(m)の物体に左側から力(F)を加えると考えます。するとこの物体は加速度(α)で運動状態が変化します。F=mαが成立しています。(図-1)
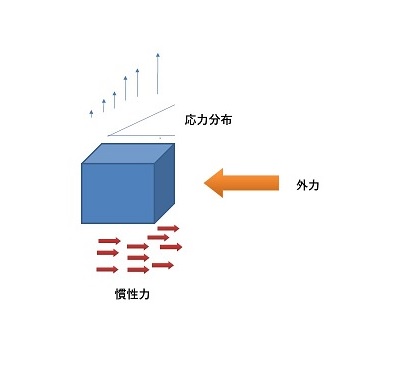
(図-1)
運動状態が変化すると同時に、この物体の内部では応力。ひずみが生じています。そして、この応力は力のかかった面で最大となり反対側ではゼロとなります。最大応力(σ)の発生している力の作用している右側の面の面積(A)とこの応力値を乗じた力が(F)に等しくなっています。
σ=F/A
mαは慣性力と呼ばれます。図-1では力が太い矢印で表されていますが、力は点や線で作用することは出来ず、必ず面を通して作用します。そしてこの外力(外から加わる力という意味でしばしば外力とも言います)は、3次元的な慣性力の集積したものとの全体で力が釣り合っているのです。
図-1で示されたように物体内部の応力状態は左側のゼロから右側のσまで連続的に変化しています。
次に、物体の左側が巨大で少しも動かない壁にあたっていると想定してください。このとき、外力(F)が加わっていますが物体は壁に阻まれて少しも動きません。加速度はゼロなのです。それでも力はかかっていて、Fに等しい力が壁からの反作用としてかかります。物体内部では最大応力であったσが内部全体に等しく生じているのです。
力が加わって、運動状態に変化がなくても物体内部には応力・ひずみが生じているのですから、力の作用として本質的な現象は運動変化よりも応力・ひずみが発生することであると言えるのではないでしょうか。
ひずみは物体を構成する分子の相対位置の微小な変化です。微小ですがひずみゲージなどを使って容易に検出することができます。大きな力が加わった時には物体自体が破壊してしまいますが、ある大きさまでは応力とひずみは比例関係にあります。その比例定数はヤング率と呼ばれ、物質ごとに決まった数値を取ります。なお、応力とは単位面積あたりの力です。
応力とひずみはの関係式はフックの法則と呼ばれ、材料力学では最も大事な式です。
σ=Eγ
ひずみは長さの相対変化ですから無次元量です。
応力は単位面積あたりの力ですから、単位の次元は[N/m^2]です。応力と圧力は同じ単位で、パスカルという名前もこの単位に与えられています。記号は[Pa]
です。Paはずいぶんと小さな値です。10^6倍にしてMPa=[N/㎜^2]ぐらいがちょうどよい大きさの次元でしょう。なお、1気圧は1013hPaです。
Fは外力ですから単位の次元は[N]です。
Aは力のかかる面積ですから、単位の次元は[m^2]です。
これらを使って、応力σの定義式は次式です。
σ=F/A
物体の両端に力Fが加わって釣り合っているとき、物体は動きませんが、長さlに変化Δlが生じます。この比率がひずみγです。
γ=Δl/l
ヤング率Eは材質によって大きく違います。一般に固い材料ほどヤング率は高いと言えます。
例えば鋼は200GPaですが金は78GPa、アルミニウムは70GPaです。
力を定義するのに物体に与えるひずみの量で決めることが自然な考えのように思われます。それには、まず材料と試験片の形状を決める必要があります。例えば、質量原器のようなイリジウムと白金の合金で物体の断面形状を決めることになるでしょう。
ただし、実務での力の測定は現状の力の測定を変えることなく、最も簡単で精度良く測れる方法を使えばよいでしょう。力の定義に応力・ひずみの関係式を用いることにすると、力はバネばかりで測ることが極めて自然なことに思えてきます。そうです、現在でも力の測定はニュートンの運動方程式には関係なく、ほとんどが原理的にバネばかりなのです。
(了)
戻る
| 