

 |

| 5年生 「割合」の学習 |
| 割合の学習は、小学校の算数学習で最もつまずきの多い単元です。 ちょっとしたアイデアで作った、割合をわかりやすくする単元です。 割合で、子どもたちがわかりにくいのは、どっちが「くらべる量」で、どっちが「もとにする量」かということです。 そして、わり算をしたのに、答えが大きくなったり、かけ算をしたのに答えが小さくなったりすることです。 |
| 単元構成のポイント |
| 1 もとにする量とくらべる量がいつでもはっきりわかる。 2 線分図が書きやすい。 3 「割合」「もとにする量」「くらべる量」の関係が図示できるため、関係をつかみやすい。 4 挑戦しながら問題をとくので、興味が持続し、意欲的に児童が取り組む。 |
どうぞこの単元構成を使って授業に取り組んでみてください。
授業では、アイテムを準備したり、小道具を用意したりして、楽しく取り組ませることが大切です。
この授業をティームティーチングで取り組むと、評価テスト平均点90点以上という夢のような成果が表れます。
| むかしむかし、ある南の島に「割合(わりあい)国」という王様の治める国がありました。たくさんの農産物や海産物のとれる豊かな国でした。 この国には、たくさんの人々が楽しく幸せにくらしていました。しかし、王様が変わり、毎月王様にみつぎものをささげるようになってから、人々のくらしはめちゃくちゃになってしまい、みんな苦しんでいました。 この「割合国」の王様は、ずいぶんわがままな王様で、人々にこんな「命令」を出したのです。 わが「割合国」では、王様がこの金の器に入れた量を「1」とする。 金の器に入っている量を「もとにする量」として、みつぎものがいくらおさめられたかは、その「何倍か」でくらべることにする。 なお、金の器に入れる量は、王様がその時勝手に決めるものとする。 なんとかってな王様でしょう。王様が、金の器に「みかん3個」をのせて、「この2倍のみかんをおさめなさい。」といったら、みかんを6個おさめればいいのです。しかし、王様が金の器に「みかん100個」をのせて、同じように「この2倍のみかんをおさめなさい。」といったら、なんと200個のみかんをおさめなくてはならないのです。 いくら、よくばりな王様だとしてもあんまりです。それに王様がかってに単位を決めてしまうのですから、人々は計算もできずにこまってしまいました。 みなさんは、ひそかにこの「割合国」にのりこみ、この王様のわがままなむずかしい問題を「割合国」の人々にかわって解決し、国民のためにもとの豊かな「割合国」をとりもどしてもらいたいのです。 |
 |
割合国で、王様の出す無理難題を解いていくためには、 割合国のことをよく知っておかねばならない。 戦いに勝つには、まず相手をよく知ることである。 <割合国の言葉を知れ!> 金の器に入っている量= (これがいつでも1)もとにする量 ↓ (何倍になるか)割合 みつぎものの量=くらべる量 <王様のくちぐせ> 割合を求めるとき 「何倍になるでしょう。」 「何倍にあたるでしょう。」 「割合はいくらでしょう。」 これは全部同じことをたずねている。だまされるな。 これが、今君たちが持っているアイテム(道具)である。 しかし、これから問題を解いていく中で、 さらにたくさんのアイテムを君たちは手に入れるであろう。 |
| 練習問題をする 数は整数で,できるだけ簡単に求められる問題にする。 図にあてはめて考える習慣をつける。 |
さあ、いよいよ「割合の世界」へタイムトリップした。君たちのかつやくに期待する。
1 アイテムにあてはめろ 2 予想はできるか 3 前の単元で使った方法を使え(線分図に書きます) 4 式を立てて、解いてみよう |
1 アイテムにあてはめて、線分図にかくのだ 2 予想はできるか 3 式をたてて、解いてみよう
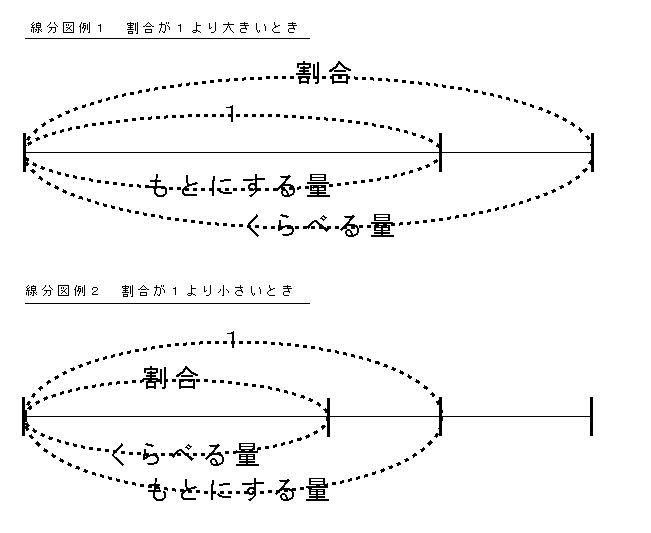
線分図をかくときのやくそく ・ 「1」と割合は線の上に書く ・ 「もとにする量」と「くらべる量」は線の下に書く |
「割合」を求める式を、言葉の式にまとめると、
| 割合 | = |
 |
| 「もとにする量」と「くらべる量」,「割合」の見分け方 「もとにする量」 ○ 金の器に入っている量 ○ 線分図では,いつでも「1」になる量 ○ 割合を考えるとき,もとになる量 ○ 線分図では下に書く。 「くらべる量」 ○ みつぎものや,金の器に入っているものとくらべる量 ○ 線分図では,割合と対になっている量 ○ もとにする量より大きくなったり,小さくなったりする。 ○ 線分図では下に書く。 「割合」 ○ もとにする量を「1」としたとき,くらべる量がその何倍かをあらわしたもの ○ 線分図では必ずくらべる量と対になる ○ 線分図では上に書く。 |
2 予想は? 3 自分の方法で解いてみよう | |
| 4 娘の持っていく量を求めよう |
「くらべる量」を求める式を、言葉の式にまとめると、
| くらべる量 | = |
| 君たちは、王様のけらいに見つかり、スパイとしてたいほされてしまいました。 王様は死刑だと言っていますが、君たちに最後のチャンスがおとずれました。 王様から、君たちへの最後のちょうせんだ。
② 予想は? ③ 自分の方法で解いてみよう |
「もとにする量」を求める式を、言葉の式にまとめると、
| もとにする量 | = |
| 君たちのおかげで、「割合国」の王様はすっかりすばらしい王様になりました。 そして、豊かな農産物をとなりの「百分率国」に売ることになったのです。
|
| 器が2こでは、どうも都合が悪いこともあるので、2つの国は話し合って、もとにする量の器は、金の器1こにすることにしました。 しかし、二つの量をくらべるのには、どちらの国の表し方が使いやすいと思いましたか。 |
| となりの国との交流もずいぶん盛んになってきました。 王様もずいぶんやさしくなったようです。
線分図 式 |
「割合の世界」9
割合国では,最近インフルエンザがはやっているそうです。
線分図 式 |
 |
「く」=くらべる量 「も」=もとにする量 「わ」=割 合 くらべる量が分からないときは,「く」をかくします。 すると, もとにする量×割合 で答えが出ることが分かります。 他が分からないときにも,同じようにこのアイテムを使います。 |
「割合の世界」10
| 国民のことを考えるようになった王様は、ある日、金の器にお城の庭600平方メートルの地図をのせて言いました。 「この庭と、さらにこの1.4倍の土地を合わせた土地を、子供達の遊園地としてつくりなおす。」 さあ、遊園地の広さはどれくらいになるのでしょう。 |
| 二つの量をくらべるのに、これはよい方法だということが、王様にはよく分かったので、 王様は、2つの量をくらべるとき、金の器はだれが使ってもよいことにしました。
|
| みなさんのおかげで,割合国は豊かな楽しい国になりました。 王様の心も変わったようですね。 みなさんも,割合の学習が楽しくできましたか。 |