（３３）相似な図形の面積と体積

１辺の長さが１ｃｍ、２ｃｍ、３ｃｍの正方形があるとき、

周の長さは、それぞれ１×４＝４ｃｍ、２×４＝８ｃｍ、３×４＝１２ｃｍとなります。
よって、辺の長さの比は、４：８：１２＝１：２：３
つまり、相似比１：２：３と同じになります。

しかし、面積はそれぞれ、１×１＝１cm２、２×２＝４cm２、３×３＝９cm２となり、
面積の比は、１：４：９＝１２：２２：３２
つまり、相似比の２乗の比と同じになります。

一般に、相似比ａ：ｂの相似な図形があるとき、 周の長さの比は、ａ：ｂ 面積の比は、ａ２：ｂ２ となります。

次に、１辺の長さが１cm、２cm、３cmの立方体があるとき、

表面積はそれぞれ、１×４＝４cm２、４×４＝１６cm２、９×４＝３６cm２となり、
表面積の比は、４：１６：３６＝１：４：９＝１２：２２：３２
つまり、相似比の２乗の比と同じになります。

しかし、体積はそれぞれ、1×1×1＝1cm３、2×2×2＝８cm３、3×3×3＝２７cm３
となり、１：８：２７＝１３：２３：３３
つまり、相似比の３乗の比と同じになります。

一般に、相似比ａ：ｂの相似な図形があるとき、 面積（表面積、底面積、速面積）の比は、ａ２：ｂ２ 体積の比は、ａ３：ｂ３ となります。

では、問題です。

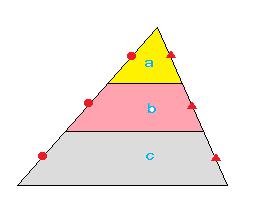
（１）下の図のように、三角形を底面と平行に２辺を３等分するように切断するとき、ａ：ｂ：ｃの面積の比を求めなさい。


（２）下の図のように、円錐の母線を３等分するように水平方向に切断したとき、ａ：ｂ：ｃの側面積の比と体積の比を求めなさい。


（３）ウルトラマンの身長は40ｍ、体重は35000トンです。これは、人間と比べて、太っているのでしょうか。やせているのでしょうか。（比重が大きいのか、小さいのかを考えてください。）（人間は、身長2ｍで、100ｋｇとします。）