四角形の3つの重心を位置ベクトルで表し、3つの重心が一致する条件を考察することで、
ベクトルの有用性を感じることが、この教材のねらいである。
「三角形の3種類の重心②」「四角形の重心と面積比」の続きで行うとよい。
なお、表記上、ベクトルは太字で表示する。

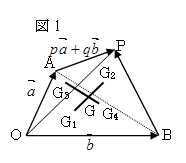
図1のような四角形OAPBに対して、基準とするベクトルを
OA=a,OB=b とし、AP=pa+qb(p>0,q>0)>とすると、
OG=(1/3)(1+s+sp)a+(1/3)(1+sq)b
s=(p+q)/(p+q+1)より、
OG=(1/3)[1+{(p+q)(1+q)/(p+q+1)}]a+(1/3)[1+{(p+q)q/(p+q+1)}]bとなる。
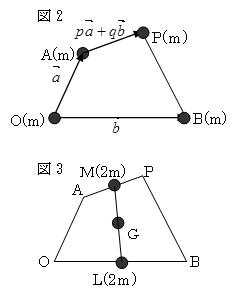
の重心だから、APの中点Lに 2m、OBの中点Mに 2m の
重さのおもりがあるときの重心より、LMの中点Gが
重心となる。
よって、OG=(OL+OM)/2=[(b/2)+a+{(pa+qb)/2}]/2
OG=(1/4)(2+p)a+(1/4)(1+q)b となる。
フレーム重心は、辺OA,辺OB,辺AP,辺PBに重さがある
ときの重心なので、それぞれの辺の中点 K,L,M,N
に、辺の長さに比例した重さ k,l,m,n のおもりがあるとして、
KMを m:k に内分する点Rに重さ k+m 、LNを n:l に内分する点S
に重さ l+n のおもりがあるときの重心となるから、
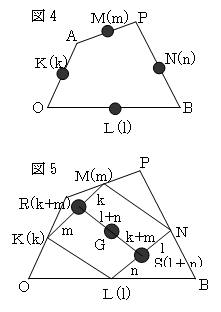
RSを l+n:k+m に内分する点Gが重心となる。
計算の都合上、AP=c,BP=dとおくと、
OR=(kOK+mOM)/(k+m)=[k(a/2)+m{a+(c/2)}]/(k+m)
={(k+2m)a+mc}/2(k+m)
OS=(lOL+nON)/(l+n)=[l(b/2)+n{b+(d/2)}]/(l+n)
={(l+2n)b+nd}/2(l+n)
よって、OG={(k+m)OR+(l+n)OS}/(k+l+m+n)
={(k+2m)a+mc+(l+2n)b+nd}/2(k+l+m+n)
ここで、c=pa+qb ,d=a-b+c
=(1+p)a+(q-1)b より、
OG={(k+2m)a+mpa+nqb+(l+2n)b+n(1+p)a+n(q-1)b}/2(k+l+m+n)
OG={k+(2+p)m+n(1+p)}a}+{l+mq+n(1-q)b}/2(k+l+m+n)
には違うことがわかる。しかし、p=0,q=1,k=l=m=n の値を代入したとき、つまり
ひし形のときは3つの重心が一致することがわかる。
p,qを具体的な数値にして計算すると易しい問題となる。