音の周波数の中にいろいろな数列が潜んでいることに興味をもち、
等差数列、等比数列、調和数列について理解を深めることが、この教材のねらいである。
ピアノやギターなどの音階と数列は、密接な関係がある。
音は空気の振動であり、その実体は音波である。この波の大きさ(振幅)が音の大きさであり、
1秒間に何回振動するかという周波数が音の高さになる。
周波数はラの音が440Hz(ヘルツ)とすることが国際的に決められていて、
(日本ではド,レ,ミ…であるが、国際的にはラからA,B,C…と、ラから始まる。)
音階と周波数の関係は、下表のようになっている。
| 音階 | ラ | ラ# | シ | ド | ド# | レ | レ# | ミ | ファ | ファ# | ソ | ソ# | ラ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 周波数(Hz) | 220 | 233 | 247 | 262 | 277 | 293 | 311 | 330 | 349 | 370 | 392 | 415 | 440 |
上表の周波数の数列はどんな関係になっているのだろうか。
また、220Hzのラを初項として、一般項を求めてみよう。
隣り合う周波数の比はこれではよく関係はわからないが、1オクターブ(ラから次のラまで)の
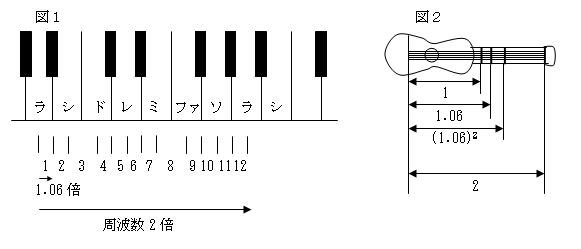
周波数は220から440とちょうど2倍になっていることがわかる。また、音階は、ピアノの鍵盤で
見ると、図1のように、ラから次のラの前までには、ラ#・シ・ド・ド#・レ・レ#・ミ・ファ・ファ#・ソ
・ソ#・ラと12個の音がある。その12個それぞれの音の周波数を調べてみると、
ある音の周波数が前の音の約1.06倍になっていることがわかる。
そして1.06倍が12回くりかえされて、1オクターブで(1.06)12≒2倍になるしくみ
となっている。つまり、この各音の周波数は公比1.06の「等比数列」である。
よって、一般項はan=220(1.06)n-1と求めることができる。
これは図2のように、ギターを押さえて振動させるときの弦の長さの比にもなっているが、
振動させる弦の長さは、音が低いほど長く、ラの音に対して1オクターブ低いラの音は、
弦の長さが倍になっている。つまり、周波数と振動させる弦の長さは、逆数の関係にある。

音には和音というものがある。Ⅰ度の和音(コードC)は「ド・ミ・ソ」、Ⅳ度の和音(コードF)は
「ファ・ラ・ド」、Ⅴ度の和音(コードG)は「ソ・シ・レ」で、この3つが主要3和音である。
この和音の3つの音の周波数の関係を調べるために、前の音階と周波数の表の周波数を11で
割って四捨五入した比、つまり、周波数440Hzのラを40としたときの主な音の周波数比を求めた
ものが下表である。ラを40として比を求めたのは、比べやすくするためである。
| 音階 | ラ | シ | ド | レ | ミ | ファ | ソ | ラ | シ | ド | レ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 周波数(Hz) | 20 | 22 | 24 | 27 | 30 | 32 | 36 | 40 | 45 | 48 | 54 |
その結果から3つの音の周波数の関係と、周波数の比の逆数である弦の長さの比をまとめたの
が下表である。
| コード | C | F | G |
|---|---|---|---|
| 和音 | ド ミ ソ | ファ ラ ド | ソ シ レ |
| 周波数の比 | 24 30 36 | 32 40 48 | 36 45 54 |
| 弦の長さの比 | 1/24 1/30 1/36 | 1/32 1/40 1/48 | 1/36 1/45 1/54 |
上表から、和音を作る3つの音の周波数にはどんな関係があるといえるだろうか?
上表から、周波数の比が、Cが公差6、Fが公差8、Gが公差9の「等差数列」になっているのが
わかる。ということはその逆数である弦の長さの比は「調和数列」ということになる。
この調和数列という名前は、このように弦の長さの比が調和数列になっているときに調和する
音が得られることからついている。