円の分割という操作的な活動を通して、数列の漸化式の理解を深め、数列を一般項で表す
必要性を感じ、数列に興味をもつことが、この教材のねらいである。
円周上にn個の点を取るとき、それらを結ぶ弦によって円はいくつの領域に分割される
だろうか。ただし、どの弦も平行でなく、また3本以上の弦が1点で交わることのないとする。

円が分割される領域の数をanとすると、
n=1のときは円は分割されないから
a1=1である。
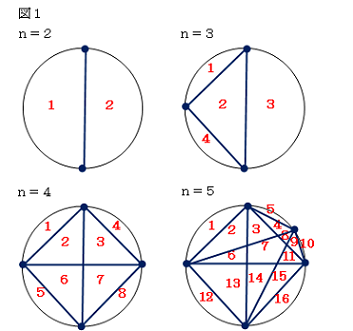
次に、n=2のときから順に図を書いて
考察してみると、図1のようになり、
領域を数えると、
a2=2,a3=4,a4=8,a5=16となる。
このことから、a6を推測させると、
a6=32で、さらにan=2n-1と推測する
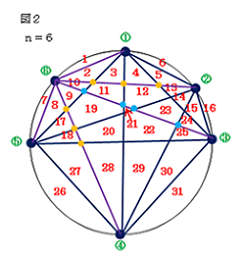
人が多いであろう。しかし、実はこれは正しくない。
実際に図2のように図を書いて、領域を数えてみる
と、a6=31となる。このしくみについて考えてみよう。
まずは円周上にとる点の数を5個から6個に増やした
ときで考える。
図2で①~⑤の点に対して⑥の点を増やしたとき、
点の番号を k とすると、
⑥の隣りの点である①に向かって弦を引いたとき、
すなわち k=1のときは、領域の数が1つ増えるだけである。
次に、⑥から⑥の2つ隣りの点②に向かって弦を引いたとき、すなわち k=2のときは、
交点の数は⑥と②の間にある1個の点①から、⑥と②以外の点③、④、⑤の3個の点に向かっ
て引く弦の数と同じになるので、交点は1×3=3個であることがわかる。
このとき、(円周上の点が5個のときにあった弦と新たに引いた弦との交点の数+1) だけ
できる領域が増えるので、領域は1+1×3=4つ増える。
また、⑥から⑥の3つ隣りの点③に向かって弦を引いたとき、すなわち k=3 のときは、
交点の数は⑥と③の間にある2個の点①と②からそれぞれ、⑥と③以外の点④、⑤の2個の点
に向かって引く弦の数と同じになるので、交点は2×2=4個であることがわかる。
このとき、領域が1+2×2=5つ増える。
同様に、k=4のときは1+3×1=4つ増え、k=5のときは1つ増える。
これを一般化すると、点の番号 k に対して、1+(k-1)(5-k)つ増えることになるから、
a6-a5=(k=1Σ5){1+(k-1)(5-k)}であることがわかる。
よって、円周上にとる点の数をn個から(n+1)個に増やしたときの漸化式は、
an+1-an=(k=1Σn){1+(k-1)(n-k)}となる。
an+1-an=n+(n3-3n2+2n)/6 と計算できるから、
この漸化式を解くと、an=a1+(k=1Σn-1){k+(k3-3k2+2k)/6 }より、
an=1+n(n-1)/2+n(n-1)(n-2)(n-3)/24 となる。
これは、an=1+nC2+nC4 と見ることのできる式である。
このnC2が弦の本数、nC4が弦と弦の交点の個数であると考えると、この式は理解できる。
この一般項から、a7を計算すると、a7=1+7C2+7C4=1+21+35=57となる。
ところで、この数列{an};{1,2,4,8,16,31,57,…}の階差数列を3回とると、
{bn};{1,2,4,8,15,26,…}
{cn};{1,2,4,7,11,…}
{dn};{1,2,3,4,…} となり、
dn=n と推測すると、
cn=1+(k=1Σn-1)k
=(1/2)(n2-n+2)
bn=1+(k=1Σn-1)(1/2)(n2-n+2)
=(1/6)(n3-3n2+8n)
an=1+(k=1Σn-1)(1/6)(n3-3n2+8n)
=(1/24)(n4-6n3+23n2-18n+24)
となり、これは、an=1+n(n-1)/2+n(n-1)(n-2)(n-3)/24 と一致する。