オウム貝や星雲、台風の雲など、いろいろな渦巻線を分析することで、平面図形に興味をもち、

単元の有用性を感じることが、この教材のねらいである。
xについての2次方程式、x2=x+1 の正の解 α=(1+√5)/2
において、1:(1+√5)/2 すなわち 1:α のことを黄金比というが、
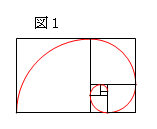
一般にオウム貝の渦巻線は、図1のように、縦と横の辺の比が
黄金比になっている長方形上に描いた「黄金らせん」と呼ばれる
らせんに近似できるといわれていて、教科書等によく紹介されて
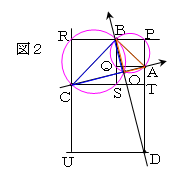
いる。ここで、図1の一部を拡大した図2において、
正方形APBQの外接円と正方形BRCSの外接円の交点をOとする
と、∠AQB=∠BSC=90°より、ABとBCはそれぞれ円の直径と、
なるので、∠AOB=∠BOC=90°となる。よって、
⊿OAB∽⊿OBCで、OA:OB=1:α であることがわかる。
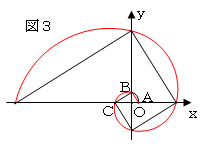
以上のことから図1の渦巻線は、AOをx軸として引くとBOがy軸
となり、図3のように、OAを90°回転させてα 倍したものが
OB、OBを90°回転させてα 倍したものがOCになる
等角らせんであることがわかる。
ただし、実際のオウム貝を調べると、等角らせんに近似
できるが、比を 1:α (α≒1.62)としたときの回転角は
150°~160°のものが多いことがわかる。
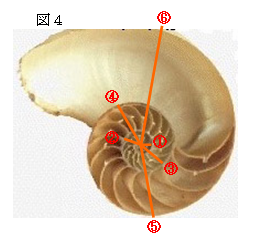
図4のオウム貝では、①から160°回転させた位置②に
対し、②の線分の長さは①の線分の長さの約1.62倍で、
②から160°回転させた位置③に対し、③の線分の長さ
は②の線分の長さの約1.62倍・・・になっている。
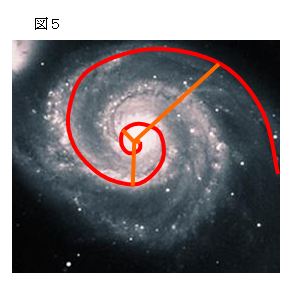
図5のM51星雲の写真の光が強い部分を渦巻線と
考えると、底角が72°の二等辺三角形を組み合わ
せて書ける図6のような渦巻線に近似できる。
この二等辺三角形は、正五角形に対角線を引いた
ときにできる二等辺三角形で、辺の比が黄金比に
なっている三角形である。
ここで図7において、⊿ACDの外接円と⊿BDEの
外接円の交点をOとすると、
∠CAD=∠DBE=108°で円周角は等しいこと
から、∠COD=∠DOE=108°となる。
よって、⊿OCD∽⊿ODEで、OC:OD=1:α であることがわかる。
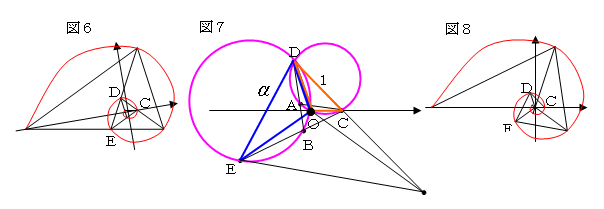
以上のことからこの渦巻線は図8のように、COをx軸として引くと、
比を α としたときの回転角が108°の等角らせんであることがわかる。
実際に調べるとM51星雲の渦巻線は、回転方向は逆であるが同じ形の、
比を α としたときの回転角が108°の等角らせんに近似できることがわかる。
図9の2003年8月7日の台風10号の写真の雲を渦巻線
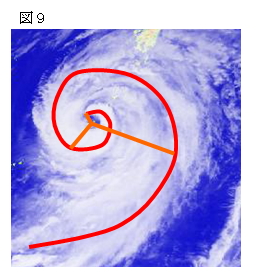
と考えると、相似比が1:α の正三角形を組み合わせて
書ける図10のような渦巻線に近似できる。この図形は
黄金比の性質であるα2=α+1を利用して描ける
面白い図形である。
ここで図11において、CDを一辺とする正三角形を
外側に書いてその頂点をR、同様にDEを一辺とする
正三角形の頂点をSとしたときに、⊿CDRの外接円と
⊿DESの外接円の交点をOとすると、∠CRD=∠DSE=60°で
円に内接する四角形の対角の和が180°であることから、
∠COD=∠DOE=120°となる。よって、
⊿OCD∽⊿ODEで、OC:OD=1:α であることがわかる。
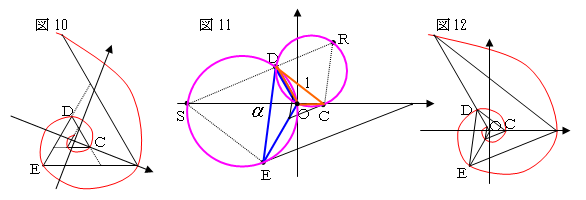
以上のことからこの渦巻線は図12のように、COをx軸として引くと、
比を α としたときの回転角が120°の等角らせんであることがわかる。
実際に調べると台風10号の雲の渦巻線は、回転方向は逆であるが同じ形の、比を α としたとき
の回転角が120°の等角らせんに近似できることがわかる。