三角形の重心の物理的な意味を探ることによって、重心に興味をもち、物理的に考えられる
3種類の重心を幾何的に分析することで、幾何のおもしろさを感じることが、この教材の
ねらいである。
数学では、三角形の3つの中線の交点のことを重心という。しかし、物理的には以下の
3種類の重心を考えることができる。

閉曲線で囲まれた図形が密度の一様な薄い素材(重さが面積に比例)
で作られているときの重心を幾何的重心という。実測重心ともいう。
図1のように、密度の一様な薄い素材でできた板をぶら下げたときの重心で、
普通、数学ではこの幾何的重心のことを「重心」と呼んでいる。
図形を構成する点に同量の重さを加えたときの平均で、慣性形における
重心を物理的重心という。質量中心ともいう。
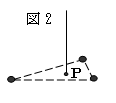
図2のように、3つの頂点に同じ重さのおもりがあり、それを結んで
いるひもや内側の板の重さは無視できるほどの重さである物体を
ぶら下げたときの重心である。
図3の直線AB上で点Aと点Bのつりあいを考えると、図4のように、Bの中点Mに2mの重さの
おもりがあるのと同じになる。次に直線MC上で点Mと点Cのつりあいを考えると、
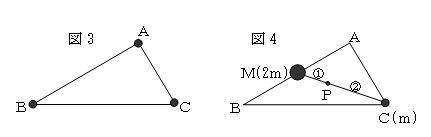
てんびんで、(支点からの距離)×(重さ)=(一定)の関係が成り立つことから、
支点の位置すなわち物理的重心Pの位置は、CMを2:1に内分する点になる。
よって、三角形の物理的重心と幾何的重心は一致する。
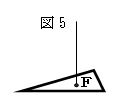
辺に重さがある図形、例えば金属フレームで作られる図形の重心を、
フレーム重心という。図5のように、3つのフレームにだけ重さがあり、
内側の板の重さは無視できるほどの重さである物体をぶら下げたときの
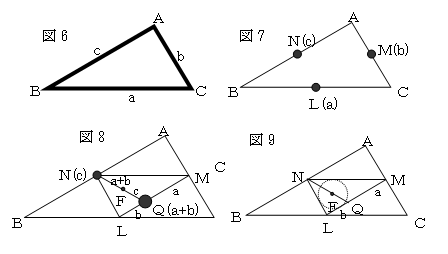
重心である。図6のように、辺a,辺b,辺cのフレームの重さをそれぞれ辺の
長さに比例させて、a,b,cとする。直線AB上で点Aと点Bのつりあいを考えると、図7のように、
ABの中点Nにcの重さのおもりがあるのと同じになる。同様に、ACの中点Mにb,BCの中点Lに
aの重さのおもりがあるのと同じになる。よって、図8のように三角形LMNを考えて、
物理的重心を求めると、MLをa:bに内分する点Qにa+bのおもりがあると考えられるので、
フレーム重心Fは、QNをc:a+bに内分する点になる。
またBC=a,AC=bより、点L,M,NはともにBC,AC,ABの中点だから、NM=a/2 ,NL=b/2より、
NM:NL=a:bで、MQ:LQ=a:bであるから、NFは∠LNMの二等分線になる。同様に考えると、
MFも∠NMLの二等分線になるので、点Fは角の二等分線の交点になる。よって図9のように、
点Fは⊿LMNの内心である。ここで⊿ABCの重心Gは⊿LMNの重心でもあり、⊿LMNの内心で
もある点Fとは、⊿LMNが正三角形のときのみ一致し、それ以外は一致しない。