円に内接する四角形の性質から、円に外接する四角形の性質、円に内接・外接する多角形の
性質と構成要素を発展させて考えることで、平面図形のおもしろさを感じることが、この教材の
ねらいである。
どんな三角形にも外接円と内接円は存在するが、四角形には必ずしも存在するとは限らない。
まず円に内接する四角形の性質を考える。円に内接する好きな四角形をいくつか書いて、
それぞれの四角形の4辺の長さと4つの角度を測ると、「円に内接する四角形の対角の和
が180°」という性質を自ら発見することができる。その後、その証明をする。
その後、逆である「対角の和が180°ならば四角形に外接円が存在する」ということを
証明する。
次に発展として、円に外接する四角形の性質を考える。同様に、円に外接する好きな四角形
をいくつか書いて、それぞれの四角形の4辺の長さと4つの角度を測ると、今度は、
「2組の対辺の長さの和が等しい」という性質を見つけることができる。

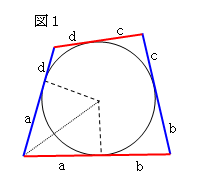
図1において、円の外部の1点から引いた2本の接線の長さが
等しいことから、2組の対辺の長さは
(a+b)+(c+d) と (b+c)+(a+d)
になるので、2組の対辺の長さの和は等しいことがわかる。
次に逆である「2組の対辺の長さの和が等しいならば
四角形に外接円が存在する」ことを証明する。
図2のように、3辺、BC=b+c,CD=c+d,DA=d+a に
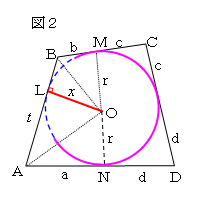
接する円を考える。円の半径 r とし、ABにOから下ろした垂線の
足をLとすると、AB=a+b ならば、ABは円に接するすなわち
OL=r であることを証明すればよい。
AL=t とおくと、OA2=ON2+AN2=r2+a2より、
OL2=OA2-AL2=r2+a2-t2
同様に、OB2=OM2+MB2=r2+b2より、
OL2=OB2-BL2=r2+b2-(a+b-t)2よって、a2-t2=b2-(a+b-t)2
2a2+2ab-2at-2btより、2(a+b)(a-t)=0 ゆえに、a>0,b>0より a=t なので、
OL2=r2+a2-t2=r2より、OL=r となる。
円に内接する四角形の性質から発展させて、円に内接する多角形の性質を考察する。
まず円に内接する六角形の性質を考えると、
「円に内接する六角形の隣り合わない内角の和は360°」
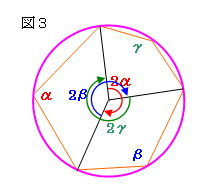
という性質があることがわかる。これは図3において、
2α+2β+2γ=720°(円周2周分)であり、
中心角と円周角の関係から、
α+β+γ=360°が成り立つことがわかる。さらに、
八角形、十角形と拡張していくと、円に内接する偶数角形
の隣り合わない内角の和は一定になり、
2n角形のとき、その和が180°×(n-1)となることがわかる。
ただし、この性質は逆は成り立たない。
円に外接する四角形の性質から発展させて、円に内接する多角形の性質を考察する。
まず円に外接する六角形の性質を考えると、
「円に外接する六角形の隣り合わない辺の長さの和どうしは等しい」
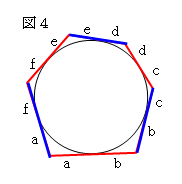
という性質があることがわかる。これは図4において、
隣り合わない辺の長さの和は、
(a+b)+(c+d)+(e+f) と (b+c)+(d+e)+(f+a)
になるので、等しいことがわかる。さらにこれも、八角形、十角形と
拡張しても同様で、偶数角形の隣り合わない辺の長さの和どうしは
等しくなる。ただし、この性質も逆は成り立たない。