将棋、囲碁などのテーブルゲームに関連する順列・組合せを計算することで、
単元の有用性を感じるのが、この教材のねらいである。
将棋の先手を決める方法は、振り駒といって、片方の人が「歩」の駒を5枚振って、
表が多かったら振った方が先手で、裏が多かったら振らなかった方が先手になる。
表が3枚以上出る確率は、(1/2)5+5C4(1/2)4(1/2)1 +5C3(1/2)3(1/2)2=(1+5+10)/32=1/2
となり、裏が3枚以上出る確率と等しい。
オセロの先手を決める方法は、伏せ石といって、コイントスのように一つの石の裏表(白黒)を
当てて決め、チェスは、両手に白と黒のポーンを隠し持ち、相手がどちらかを選んで決める
ので(チェスは白が先手)、ともに将棋と同じで、確率は1/2ずつである。
囲碁の先手を決める方法は、握りといって、片方の人が「白石」を無作為に取って(必ず
1個は取る)、もう片方の人が取った白石が奇数個か偶数個かを当てる方法で決める。
当てる方は、奇数だと思ったら盤上に黒石を1個置き、偶数だと思ったら盤上に黒石を2個
置く。当たれば先手、外れれば後手となる。
白石が全部でn個あるとすると、取り方は全部で2n-1通りあり(0個取る場合がないので)、
そのうち奇数個取る取り方は2n-1通り、偶数個取る取り方は2n-1-1通りで、偶数個取る確率の方が、0個取る場合がない分、ほんのわずかであるが小さく、
将棋、オセロ、チェスと違って、厳密にいえば1/2ではない。
(無作為でなく、意識して奇数個取るかか偶数個取るか決めて取ってしまうと、
奇数個取る確率と偶数個取る確率は同じになってしまうと思われる。)
わからない場合は、全部で白石が5個しかないときくらいから考察してみてもよい。
全部で白石が5個のとき、奇数個取る確率は24/25-1=16/31(約51.6%)、
偶数個取る確率は24-1/25-1=15/31(約48.4%)となる。
実験してみるのもおもしろいが、石が多すぎると相対度数に差がでないし、
逆に石が少なすぎると無作為に取れないので難しい。
麻雀で親を決めるとき、まず仮仮親を決め、そこからさいころ2個を2回振って決めることが多

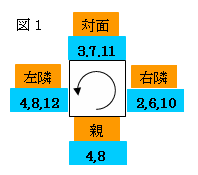
い。まず仮仮親の人がさいころ2個振って、右回りに図1のように
2,6,10なら右隣、3,7,11なら対面、4,8,12なら左隣、5,9なら自分
が仮親になり、次に仮親がもう一度さいころを振り、仮親から見て
2,6,10なら右隣、3,7,11なら対面、4,8,12なら左隣、5,9なら自分
が親に決定する。さいころ2個を1回振ったとき、
親が右隣に移る(2,6,10が出る)確率は(1+5+3)/36=9/36=1/4
親が対面に移る(3,7,11が出る)確率は(2+6+2)/36=10/36=5/18
親が左隣に移る(4,8,12が出る)確率は(3+5+1)/36=9/36=1/4
親が自分のままの(5,9が出る)確率は(4+4)/36=8/36=2/9なので、
さいころ2個を2回振った後、親になる確率は、最初に自分が
仮仮親のとき、(2/9)×(2/9)+(5/18)×(5/18)+(1/4)×(1/4)+(1/4)×(1/4)=163/648
仮仮親の対面のとき、(2/9)×(5/18)+(5/18)×(2/9)+(1/4)×(1/4)+(1/4)×(1/4)=161/648
仮仮親の左右のとき、(2/9)×(1/4)+(5/18)×(1/4)+(1/4)×(2/9)+(1/4)×(5/18)=162/648
となり、初めに仮仮親になった人がわずかながら親になる確率が高いことがわかる。