すごろくの確率を分析することで、反復試行について理解し、単元の有用性を感じることが、
この教材のねらいである。
すごろくで、止まりたいマスがあるとき、そのマスから何マス離れている所にいるときが
一番止まる確率が高いだろうか?
止まれるのは1が出たときだけなので、確率は1/6(≒16.7%)である。
止まれるのは、2が出たときと、2回振って(1,1)と出たときなので、
確率は、1/6+(1/6)2=7/62=7/36(≒19.4%)である。
止まれるのは、3が出たときと、2回振って(1,2)か(2,1)、3回振って(1,1,1)と出たときなので、
確率は、1/6+2C1(1/6)2+(1/6)3=(1/6){1+(1/6)}2=72/63=49/216(≒22.7%)である。
同様に考えると、確率は、1/6+3C1(1/6)2+3C2(1/6)3+(1/6)4=(1/6){1+(1/6)}3
=73/64=343/1296(≒26.5%)である。
同様に考えると、確率は、74/65=2401/7776(≒30.9%)である。
同様に考えると、確率は、75/66=16807/46656(≒36.0%)である。
これは、「さいころを6回振ったとき、何回目かにそれまで出た数の総和が6になる確率を
求めよ。」という問題で、この問題は数学オリンピックの過去問で、2009年の高校生クイズ
(日本テレビ)の番組でも出題されている。
①~⑥の確率を見てわかるように、二項定理から、n回振ったときに総和がnになる確率は、
1≦n≦6のとき、(1/6){1+(1/6)}n-1=7n-1/6nになることがわかる。
7の目は出ないので、76/67-(1/6)=(76-66)/67=70993/279936(≒25.4%)となり、
7マス離れると、6マス離れているときよりも確率は下がることがわかる。
なお、「1の目かつ⑥が起こる」または「2の目かつ⑤が起こる」または・・・と考えて、
(1/6)×(65+7×64+72×63+73×62+74×6+75)/66でも同じ答えが出る。
これは、①~⑥の平均(期待値)といえる。
同様に、「1の目かつ⑦が起こる」または「2の目かつ⑥が起こる」または・・・といえるので、
②~⑦の平均をとればよく、計算すると、450295/1679616(≒26.8%)となる。
②~⑦のうち、⑥(6マス離れているとき)が最大なので、8マス離れているときの確率も、
6マス離れているときを超えることはないことがわかる。同様に考えていくと、
6マス離れているところにいるときが一番止まる確率が高いことがわかる。
これを表計算ソフトを用いて、繰り返して計算していくと、nマス離れているときの確率はn→∞で
28.57%に収束していき、nが100マスを超えたくらいで、2/7の値に小数第10位まで近似する。
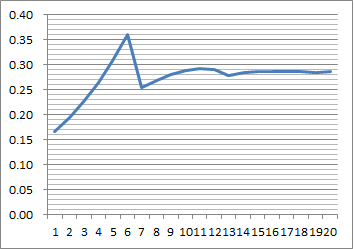
| nマス | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 止まる確率 | 0.167 | 0.194 | 0.227 | 0.265 | 0.309 | 0.360 | 0.254 | 0.268 | 0.280 | 0.289 | 0.293 | 0.290 |

以上が、それを表とグラフで表したものである。
まとめると、nマス離れているときの確率は、以下のような関係式になる。
an=7n-1/6n (1≦n≦6)
an=(an-6+an-5+an-4+an-3+an-2+an-1)/6 (7≦n)
この漸化式を解いてn→∞の極限を取ると、2/7に収束することが予想できるが、
正しいかは不明である。