しきつめられる正多角形について考察することから、約数の利用や整数解の方程式に
興味をもち、単元の有用性を感じるのが、この教材のねらいである。
身の回りからしきつめ模様を探し、それをもとに考察し、平面をしきつめられる正多角形は、
正三角形、正方形、正六角形の3つしかないことを示す。
正 n 角形の一角の大きさは、180(n-2)/nである。これがしきつめられるには、
この角が m 個集まったものが360°になればよいので、m×180(n-2)/n=360 となる。
これを解くと、mn-2m-2n=0から、両辺に 4 を足して左辺を因数分解すると、
(m-2)(n-2)=4となり、n-2 は正の整数であることから、n-2=1,2,4 となり、
n=3,4,6 となることがわかる。
なお、平面をしきつめられる正多角形は、

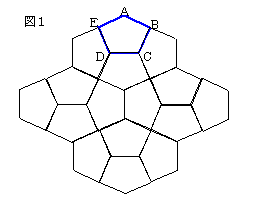
5辺が同じ長さのある図1のような五角形
(等辺五角形)はしきつめることができる。
この等辺五角形は、∠A=131.34°、
∠B=∠E=90°、∠C=∠D=114.33°で、
5つの辺の長さが等しい五角形である。
図1のようにしきつめられるので、実際に
しきつめを体験してもおもしろい。