重心の条件を三角形から四角形に拡張することで創造性を培い、重心に興味をもち、
単元の有用性とおもしろさを感じることが、この教材のねらいである。

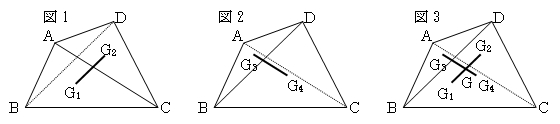
まず、図1のように四角形ABCDを⊿ABCと⊿ACDに分けて、それぞれの三角形の重心
G1,G2を作図すると、四角形の重心Gは線分G1G2上に存在する。
次に、図2のように四角形ABCDを⊿ABDと⊿BCDに分けて、それぞれの三角形の重心
G3,G4を作図すると、四角形の重心Gは線分G3G4上に存在する。
よって、図3のように、四角形の重心Gは、線分G1G2と線分G3G4との交点となる。
四角形の重心の求め方について考察すると、次のような順で意見がでて、正解にたどりつく
ことが多い。
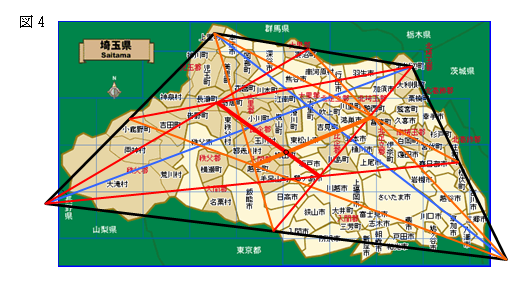
埼玉県の外形を四角形に近似して、埼玉県の重心を求めてみると、図4のようになる。
これによると埼玉県の重心は鳩山町になる。なお、以前国土地理院で計算して発表していた
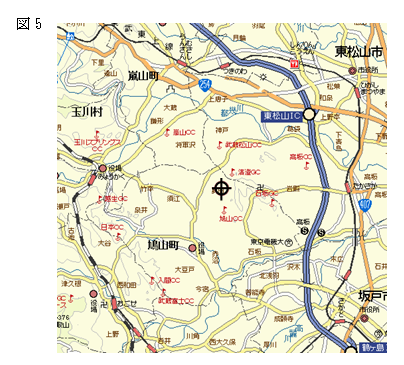
埼玉県の重心は、北緯35°59′59″,東経139°20′40″、埼玉県比企郡鳩山町奥田で、
鳩山カントリークラブの北側の山中で、図5の中心(マーク)で示したところである。
実際に作業させたり、厚紙を埼玉県の形に切り抜き、重心でぶら下げてみたりするとおもしろ
い。