平面図形の性質を利用して√abの長さを作図することで、平面図形や作図に興味をもち、
単元の有用性を感じることが、この教材のねらいである。
横の長さがa、縦の長さがbの長方形がある。この長方形と同じ面積の正方形を、
定規とコンパスだけで作図せよ。
(a+b)2-(a-b)2=4abより、
(a+b)2-(a-b)2=(2√ab) 2と考え、この式を利用する。
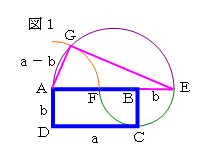
まず、縦a-b、斜辺a+bの直角三角形を次の手順で作図する。
①図1のような横の長さがa 、縦の長さがbの長方形ABCDにおいて、

コンパスを利用して点Bを中心とする半径bの円弧を作図し、
円弧と線分ABをB側に延長した直線ABとの交点をEとする
と、AE=a+bとなる。
②円弧と線分ABとの交点をFとすると、AF=a-bとなるので、
コンパスを利用して点Aを中心とする半径a-bの円弧
を作図する。
③ABの中点をとってAEを直径とする円弧を作図し、②で描いた円弧との
交点をGとすると、直径に対する円周角の性質から、
AG=a-b、∠AGE=90°となる。
よって、縦a-b、斜辺a+bの直角三角形が作図できる。
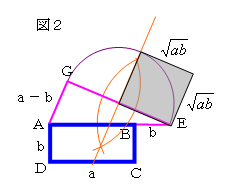
(a+b)2-(a-b)2=(2√ab) 2より、
三平方の定理から、EG=2√abとなる。
よって図2のように、EGの中点Mを作図して、
点Mを中心とする半径√abの円弧を描くと、一辺が√abの正方形を作図することができる。