トランプのポーカーに関連する組合せを計算し、役の作りやすさについて考察することで、
確率について理解を深め、単元の有用性を感じるのが、この教材のねらいである。

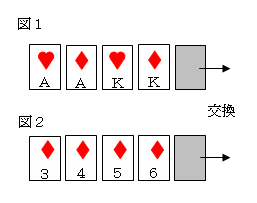
トランプのポーカーで、最初の手札が図1のようなとき、
フルハウス(3枚組+2枚組)になる
確率は、トランプはジョーカーを除くと全部で52枚
なので、52-5=47より、残り47枚中、
A(残り2枚)またはK(残り2枚)を引けばよく、
Aを引くという事象とKを引くという事象は排反(同時に起きない)なので、
2/47+2/47=4/47の確率でフルハウスができることがわかる。
次に、最初の手札が図2のようなとき、1枚交換して
ストレート(数字が5枚つながる)またはフラッシュ(5枚全てマークが同じ)になる確率は、
残り47枚中、ストレートの場合は2か7(マークが4種類)の残り8枚を引けばよく、
フラッシュの場合は◇の残り9枚を引けばよいが、この2つの事象は排反でなく、
◇2か◇7を引く場合が重なっているので、8/47+9/47-2/47=15/47の確率で
ストレートまたはフラッシュができることがわかる。
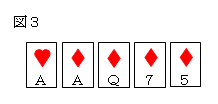
最初の手札が図3のように、4枚が同じマークで残り1枚が
違うマークのワンペアーができている場合、
フラッシュを狙ってマークの違う1枚を交換した方が
よいか、それともワンペアーをいかして他の3枚を交換
した方がよいかはよく悩むところである。そこで、どちらの方が確率が高いかを求めてみよう。
フラッシュができる確率は、◇は残り9枚なので、9/47である。
フラッシュができない場合でも、フラッシュを狙ったときに、何か役ができる確率を考えると、
ワンペアーができる確率は、Q,7,5が残り3枚、Aが残り2枚あるので、
(3×3+2)/47=11/47となり、
フラッシュができる事象とワンペアーができる事象は排反なので、
フラッシュまたはワンペアーができる確率は、確率の加法定理より、
9/47+11/47=20/47(≒42.5%)となる。
ワンペアーを残すので、役ができる確率は100%。
ツーペアーになる確率は、A以外のもうワンペアーがA,5,7,Q以外の9種類のときと、
5,7,Qのときと場合分けして、(4C2×43×9+3C2×44×3)/47C3=906/5405(≒16.8%)
スリーカードになる確率は、Aをもう一枚だけ引けばよいので、
(2C1×45C2)/47C3=132/1081(≒12.2%)
フルハウスになる確率は、ツーペアーの場合に加え、Aかもう片方かのどちらかが3枚になれば
よいので、{(4C2×2C1+4C3)×9+(3C2×2C1+3C3)×3}/47C3=11/1081(≒1.0%)
フォーカードになる確率は、Aを二枚引かなくてはならないので、
(2C2×45)/47C3=3/1081(≒0.3%)
ワンペアーを残した場合、役ができる確率は100%だが、フラッシュ以上の役ができる確率は、
11/1081+3/1081=14/1081とわずか約1.3%しかないことがわかる。
実際に実験をやって、相対度数と確率を比較してみてもおもしろい。