身近にある虹のしくみを、平面図形のいろいろな性質を利用して分析することで、単元の有用
性を感じ、いろいろな解法で角度を求めることで図形の見方を広げることが、この教材のねらい
である。
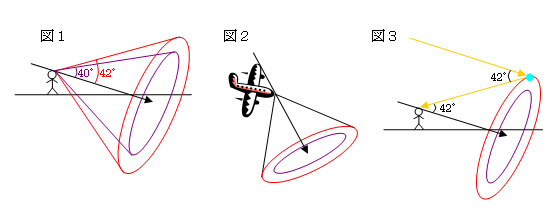
虹は図1のように、太陽光線を軸にした頂角42°の円錐の底面に円状にできる。
42°の部分は赤色の光で、虹の一番上の色になる。内側の円は頂角40°の円錐の底面となり、
これは紫色の光で、虹の一番下の色になる。虹は本来は円状であるが、地平線の下に隠れる
ため扇形の円弧に見える。よって図2のように、条件が揃い飛行機上などから見下ろした場合、
円上に見える。虹の赤色の部分が42°の円錐の底面に円状にできる理由は、図3のように、
太陽光線が空気中の水滴の粒に当たって反射する赤色の光のうち、42°で反射する赤色の光
が一番強いからである。色によって屈折率が違うため、紫色の光は、40°で反射する光が一番
強く、それによって虹は多色に見えるのである。

このようなしくみから、次のようなことがわかる。
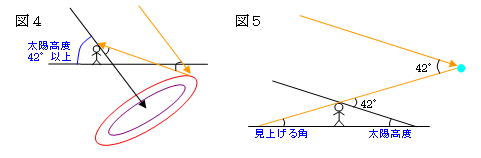
太陽光線が空気中の水滴の粒に当たって反射する光のうち、42°で反射する光が一番強い
理由について分析する。
水滴の粒を円と仮定し、太陽光線が水滴の粒に入射する角を α 、屈折して出る角を β
とすると、光の反射は図6のように、A→B→C→D→Eと進む。
このとき、∠ABC=180°-α+β ,∠BCD=2β ,∠CDE=180°-α+β より、
太陽光線が水滴の粒に当たって反射してくる光の角度を θ とすると、
θ=∠ABC+∠BCD+∠CDE-360°=4β-2α となる。
ここで α と β の関係は、赤色の光の場合、空気の絶対屈折率と水の絶対屈折率の関係から、
屈折の法則より、図7において(sinα/sinβ)=4/3 とすると、sinβ=(4/3)sinα から、
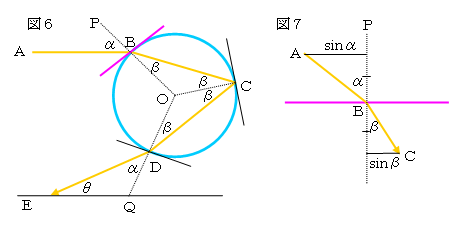
β=sin-1{(3/4)sinα} となる。よって、θ=4sin-1{(3/4)sinα}-2α となる。ここで入射角 α を
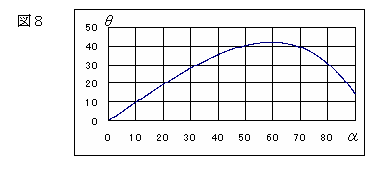
0°から90°まで変化させると、図8のグラフより、α≒60°のとき、θが最大値となる。
この最大値付近が一番たくさん赤色の光が集まるため、α≒60°のとき、赤色の光が
一番強くなることがわかる。
α=60°のとき最大とすると、sinβ≒(3/4)sin60°=(3√3/8)=0.6495より、β≒40.5となる。
α=60°のとき、β=40.5°とすると、このときの赤色の光の反射の様子は図9のようになる。
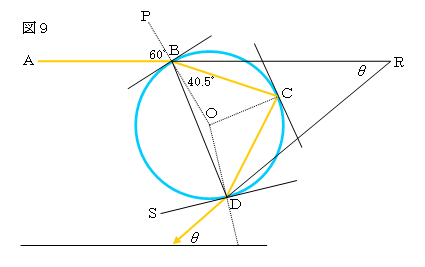
∠ABP=∠EDQ=60°、∠OBC=∠BCO=∠OCD=∠CDO=40.5°がわかっているとき、
θ=∠BRD=∠DEQを求める。この問題はいくつかの解法が考えられる。
①接弦定理の利用
∠BDS=∠BCD=∠BCO×2=40.5°×2=81°(接弦定理)より、
∠BDO=∠ODS-∠BDS=90°-81°=9°。よって、∠BDC=40.5°+9°=49.5°
∠CDR=∠ODR-∠ODC=∠QDE-∠ODC=60°-40.5°=19.5°より、
∠BDR=49.5°+19.5°=69°
同様に、∠DBR=69°なので、⊿BRDにおいて、∠BRD=180°-(69°×2)=42°
②円周角の定理の利用
∠BCD=81°より、∠BOD=162°(円周角の定理)
⊿BODは二等辺三角形なので、∠BDO=9°より∠BDC=49.5°以下は①と同様。
③二等辺三角形の性質を利用
⊿BODは二等辺三角形で∠OBD=∠ODBより、⊿BCDは二等辺三角形
よって、∠BDC=(180°-81°)÷2=49.5°以下は①と同様。
よって、θ=42°となり、赤色の光は42°のところに集まるため、42°のところに見える。
また、紫色の光は屈折率の違いから40°のところに集まるため、40°のところに見え、
各色の屈折率の違いから虹となって見える。また、40°から42°以外のところは、
各色の光が弱くまた各色が重なるため、白色になってしまい見えないと考えられる。
虹にはいくつか種類があって、いままで扱ってきた太陽光線が水滴の粒の中で1回だけ
反射する虹を主虹というのに対して、水滴の粒の中で2回反射する虹を副虹という。
副虹は主虹ほどはっきり見えないが、条件がよければ見ることができる。反射の様子は
図10のようになる。
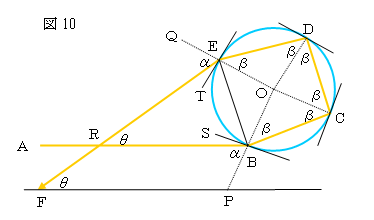
赤色の光の反射はA→B→C→D→E→Fと進み、θ=6β-2αより、θ=6sin-1{(3/4)sinα}-2α
となる。よって、α≒72°のとき、β≒45.5となり、これが今度はθの最小値となる。
つまり、α≒72°のとき、赤色の光が一番強くなることがわかる。ここで、
∠ABP=∠FEQ=72°、∠OBC=∠BCO=∠OCD=∠CDO=∠ODE=∠DEO =45.5°
とするとき、θ=∠BREを求める。
∠OBE=180°-(3×45.5°)=43.5°(円に内接する四角形の対角の和は180°)
よって、∠EBS=90°-43.5°=46.5°、∠RBS=90°-∠ABP=90°-72°=18°より、
∠EBR=46.5°+18°=64.5°同様に、∠REB=64.5°より、
∠BRE=180°-(64.5°×2)=51°
よって、θ=51°となり、副虹の赤色の光は51°のところに見える。
また、紫色の光は53°のところに見え、副虹は反射してひっくりかえるため、
虹の見え方が逆になる。
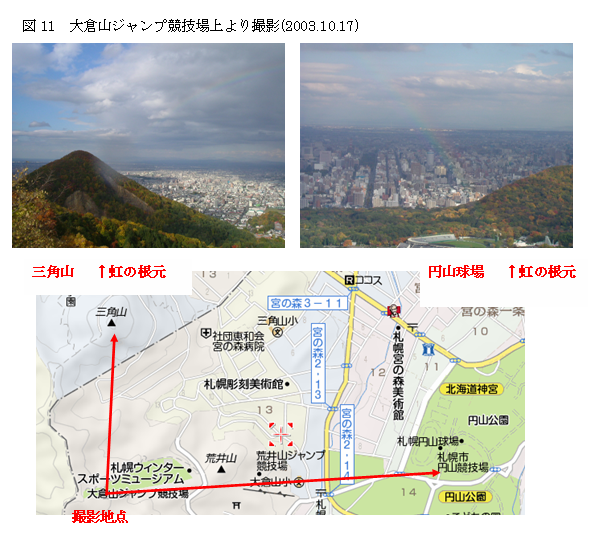
実際に札幌市の大倉山ジャンプ競技場の上で虹の写真を撮ったとき、写真と地図で調べると、
図11のように、虹の根元が三角山と円山球場にあり、その3点を結んだなす角を測ると約84°
である。つまり、虹は約42°の円錐の底面の円状にできていた。虹ができたとき、実際に
調べてみるとよい。