道順問題を通して、同じものを含む順列について深く理解し、単元の有用性を感じることが、
この教材のねらいである。
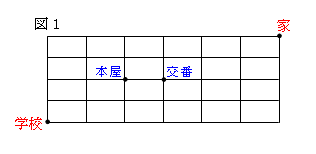
図1のように、東西に5本、南北に7本の道がある。このとき、次の場合で最短距離
で帰る道順は何通りあるか。
①学校から家に帰る。
②学校から本屋によって家に帰る。
③本屋と交番の間の道が通行止めの場合に、学校から家に帰る。

北に1区画進むことを↑、
東に1区画進むことを→で表すと、
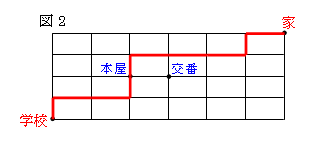
例えば、図2の赤線で示された道順は、
↑→→↑↑→→→↑→で表すことができる。
よって、①の「学校から家に最短距離で行く
道順の総数」は、4個の↑と6個の→を1列に並べる同じものを含む順列
となるので、10!/(4!×6!)=210通りとなる。
別の考え方として、これを組合せを使って
考えてみる。
学校から家に帰るRPGゲームと考えると、
矢印ボタンを10回押して移動するとき、
「上矢印(↑)を何番目に押すか?」と考えると、
上矢印ボタンを押す所を、10ヶ所から4ヶ所選べばよいので、10C4=210通りとなる。
②の問題は、「学校から本屋に行く」かつ「本屋から家に帰る」と考えればよいので、
4C2×6C2=90通り。
③の問題は、通行止めの道を通る場合を考え、それを全体(①)から引くことで、
通行止めの道を通らない場合が求められる。
まず「学校から本屋に行く」かつ「交番から通行止めの道を通って交番に行く」
かつ「交番から家に帰る」と考えて、
4C2×1×5C2=60より、210-60=150通りとなる。
平面の道順の問題を拡張して、空間の道順を考えてみよう。
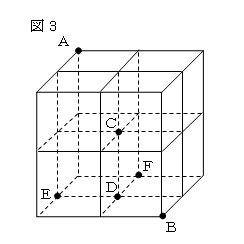
図3のように、1辺が1の立方体が8個積まれた、1辺が2の立方体がある。
このとき、次の場合で最短距離で進む道順は何通りあるか。
①AからBに進む。
②Aから、立方体の表面だけを通って(内部を通らずに)Bに進む。
③Aから、立方体を置いたときに見える面だけを通って(内部と下面を通らずに)Bに進む。
「角砂糖のまわりを蟻が進む」という設定にすると
おもしろい。①の問題は、縦矢印と横矢印と高さ矢印
の3方向の矢印2個ずつを1列に並べる同じものを含む
順列と考えればよい。RPG風でいうと、
全6回のうち3種類のボタンを2回ずつ押せばよいので、
6C2×4C2=90通りとなる。
②の問題は、まず立方体の内部つまり点Cを通る場合
を考え、それを全体(①)から引けばよいので、
「AからCに行く」かつ「CからBに行く」で、(3C1×2C1)×(3C1×2C1)=36より、
90-36=54通りとなる。
③の問題は、まさに蟻が机の上に置いてある角砂糖の表面を進むという設定となるが、
②から、さらに立方体の下部つまり点Dを通る場合を引けばよい。
点Dを通るためには、点Eか点Fを通らなくてはならないので、
「AからEに行く」かつ「EからDに行く」かつ「DからBに行く」という場合が、3C1×1×2C1=6通り、
「AからFに行く」かつ「FからDに行く」かつ「DからBに行く」という場合も、3C1×1×2C1=6通り
なので、54-(6+6)=42通りとなる。