三角形の成立条件を自ら発見することで、成立条件の理解を深め、図形のおもしろさを
感じるのが、この教材のねらいである。
紙や割り箸などで長さが2,3,4,5,6cmの5個の辺を作り、その中から3個選んで三角形を作る
実験を行う。そして、全部で10通りの組合せのうち、どの組合せが三角形ができるかを調べる。
a<b<c として3つの辺の長さを(a,b,c)で表すとすると、
三角形ができる組合せは、(2,3,4)(2,4,5)(2,5,6)(3,4,5)(3,4,6)(3,5,6)(4,5,6)の7通りであり、
できない組合せは、(2,3,5)(2,3,6)(2,4,6)の3通りである。
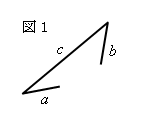
3つの辺の長さに着目して考察すると、三角形ができる条件は、c<a+bであることがわかる。

これは図1より、c≧a+b のときは2辺が届かず、三角形ができない
ことからわかる。
また、c<a+b の式を変形すると、c-a<b,c-b<aであることから
(a<b+c,b<a+c,b-a<cは明らかなので)、
三角形の成立条件は、
とすることができる。
また、ここから三角形の成立条件の式、|a-b|<c<a+b を導くことができる。