３つの角が直角の三角形

back

ユークリッド幾何学と非ユークリッド幾何学

「三角形の内角の和が180°でない三角形がある」など、非ユークリッド幾何学の話を通して、

幾何学に興味をもつことが、この教材のねらいである。

①ユークリッド幾何学

高校までで学ぶ幾何学はユークリッド幾何学である。

その中で次の定理について考察する。

1. 直線外の点を通りその直線に平行な直線は１本だけ引ける。（平行線は交わらない。）
2. 三角形の内角の和が180°である。

②楕円幾何学

ユークリッド幾何学が成り立たないとして成立する幾何学を非ユークリッド幾何学という。

非ユークリッド幾何学は大きく分けて２つあるが、１つ目は、リーマン(ドイツ1826～)が

考えた、楕円幾何学である。これは、楕円体の表面での幾何学で、

1. 直線外の点を通りその直線に平行な直線は１本も存在しない。（必ず１点で交わる）
2. 三角形の内角の和が180°より大きい。

である。

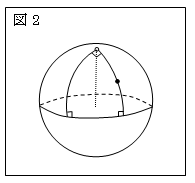
例えば、楕円幾何学の中の球面幾何学のモデル

として、地球をイメージするとわかりやすい。

地球上では、図2のように異なった２地点にいる

２人が北に平行に進むと必ず北極点で会う（交わる）し、

２つの経線と赤道を結ぶ三角形は３つの角がすべて90°で、

内角の和は270°である。

③双曲幾何学

非ユークリッド幾何学は大きく分けて２つ目は、ロバチェフスキー(ロシア1793～)と

ボヤイ(ハンガリー1802～)が考えた、双曲幾何学である。

これは、双曲面での幾何学で、

1. 直線外の点を通りその直線に平行な直線は無数に存在する。
2. 三角形の内角の和が180°より小さい。

である。

モデルとしてベルトラミーの擬球面などがあるが、これをイメージするのは難しいので、

存在だけを話す程度でよいだろう。

(参考文献)

[1] 中宮寺薫(1994)，『数学通になる本』，オーエス出版社，pp.42-48．