現実の問題を解決する場面で三角形の外心を用いることで、外心の理解を深め、
外心に興味をもち、単元の有用性を感じることが、この教材のねらいである。
3つの点から等距離にある点は、その3つの頂点からなる三角形の3辺の垂直二等分線
の交点であり、その点を外心という。これを利用した現実問題の解決を考える。
また問題解決を通して、鋭角三角形の外心は三角形の内部にあり、鈍角三角形の外心は
三角形の外部にあることを実感したり、最短シュタイナー問題にまで発展したりする。
Aさんは仕事の関係で利用する駅が日によって違うため、その3つの駅の
のどの駅からも便利な場所に住もうと考えました。どこに住めばよいでしょうか?

<3つの駅を結んでできる三角形が鋭角三角形のとき>
「どの駅からも便利な場所」というあいまいな問いに対して、
3つの駅を結ぶ三角形が鋭角三角形ならば、
「3地点から等距離な場所に住む」という考えが出ることが
予想される。それは直感的に、3地点から等距離な点が
三角形の内部にくるからである。
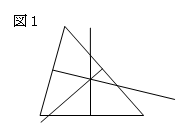
そこで2地点から等距離な点が垂直二等分線上にある
ことを利用して、図1のような外心を作図する。
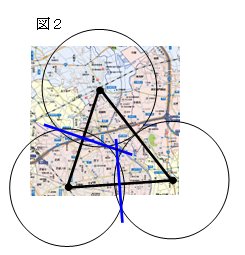
実際の作業は図2のように適当な地図を与えて行う
とよい。
垂直二等分線はコンパスを利用して作図できるとよい。
<3つの駅を結んでできる三角形が鈍角三角形のとき>
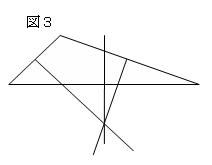
3つの駅を結ぶ三角形が鈍角三角形のときは、
3地点から等距離な点は図3のように三角形の外部にくる。
このとき、「どの駅からも便利な場所」が果たして
「3地点から距離な場所」だろうか?という疑問が出る。
そこで、「どのような場所が、どの駅からも便利な場所
だろうか?」を考えてみることにする。
三角形の3地点からの距離の和が最小になるような点を求めるような問題は
「最短シュタイナー問題」といわれている。3地点をネットワークで結ぶときに、
どのように結べばよいかを考える問題である。
「どの駅からも便利な場所」に、「どの駅にも同じ頻度で行くならば、3つの駅までの
距離の和が最小である場所が便利な場所である」という考えが出るだろう。
<ヴィヴィアーニの定理>
「正三角形の内部の点から3辺までの距離の和が一定である。」
という定理をヴィヴィアーニの定理という。まず、この定理を証明する。
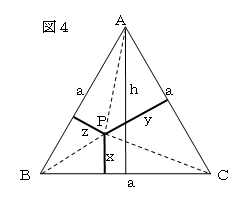
図4において、正三角形の一辺の長さをa、正三角形の
BCを底辺としたときの高さをhとする。三角形の内部の
任意の点Pについて、三角形の面積に着目すると、
⊿PBC+⊿PCA+⊿PAB=⊿ABCより
(1/2)ax+(1/2)ay+(1/2)az=(1/2)ah
よって、x+y+z=h(一定)
ゆえに、点Pが三角形の内部のどこにあっても、
正三角形の内部の点Pから3辺までの距離の和は一定である。
<最大角が120°未満の三角形の最短シュタイナー問題>
最大角が120°未満の三角形ABCにおいて、図5の∠AQB=∠BQC=∠CQA=120°
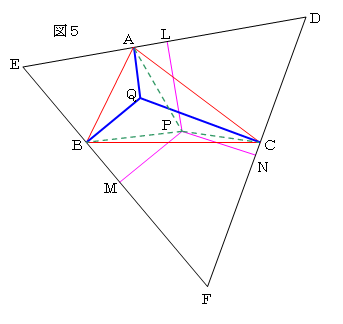
となる点Qは、3頂点からの距離の
和AQ+BQ+CQが最小になるような点
である。このことを証明する。
⊿ABCにおいて、AQ⊥DE,BQ⊥EF,
CQ⊥DFになるように三角形DEFを書くと、
∠AQB=∠BQC=∠CQA=120°から
∠AEB=∠BFC=∠CDA=60°となり
⊿DEFは正三角形となる。
ここで、⊿ABCの内部の任意の点Pから
DE,EF,DFに下ろした垂線をそれぞれ
PL,PM,PNとすると、⊿DEFは正三角形なので、ヴィヴィアーニの定理から、
AQ+BQ+CQ=PL+PM+PN・・①
ここで、AP≧PL,BP≧PM,CP≧PNなので、AP+BP+CP≧PL+PM+PN・・②
①,②から,どんな点PにおいてもAP+BP+CP≧AQ+BQ+CQ がいえるので、
点Qは3頂点からの距離の和が最小になる点である。
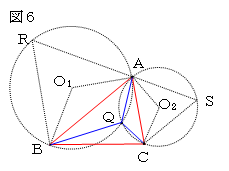
点Qの作図については、図6のようにできる。三角形ABCの
外側に正三角形を作って、その正三角形の外接円の交点
をQとすると、∠ARB=∠CSA=60°であることから、円の
内接四角形の性質より∠AQB=∠BQC=∠CQA=120°
となることがわかる。
円の内接四角形の性質はこの後の学習内容であるので、
それを使わない場合には円周角と中心角の関係より、∠AO1B=∠CO2A=120°から、
弧ARBに対する中心角∠AO1B=240°、弧CSAに対する中心角∠CO2A=240°より、
∠AQB=∠BQC=∠CQA=120°とすればよい。
<最大角が120°以上の三角形の最短シュタイナー問題>
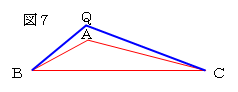
に、∠BQC=120°の点は三角形の外部に出てしまうため、
∠AQB=∠BQC=∠CQA=120°となる点は存在しない。
この場合、3頂点からの距離の和が最小になる点は頂点Aになる。このことを証明する。
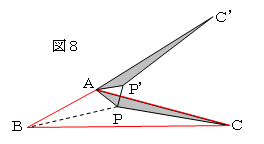
図8のように、任意の点Pにおいて、BAの延長線上に
AC=AC’になるように点C’をとり、
⊿APC=⊿AP’C’になるように点P’をとると、
∠BAC≧120°から、∠PAP’=∠CAC’≦60°より、
PP’≦PA,PC=P’C’より、BP+AP+CP≧BP+PP’+P’C’
図8より、BP+PP’+P’C’≧BC’=BA+AC’=BA+AC
ゆえに、BP+AP+CP≧BA+ACとなり、BA+ACが最小となる。
「どの駅からも便利な場所」について考えられるもう一つの考え方に、「3つのすべての駅に行く
ことを考えて、どの駅にいく場合でもある一定の距離以内である。」という考えもある。
例えば、不動産のちらしに以下のような物件が3つあったとき、どの駅も同じ頻度で使わなくては
ならない人は地理的にどれを選ぶだろうか。
| 物件A | 物件B | 物件C | |
|---|---|---|---|
| 蕨駅まで | 1.72km | 0.27km | 1.47km |
| 戸田公園駅まで | 1.72km | 1.43km | 1.68km |
| 南鳩ヶ谷駅まで | 1.72km | 2.58km | 1.68km |
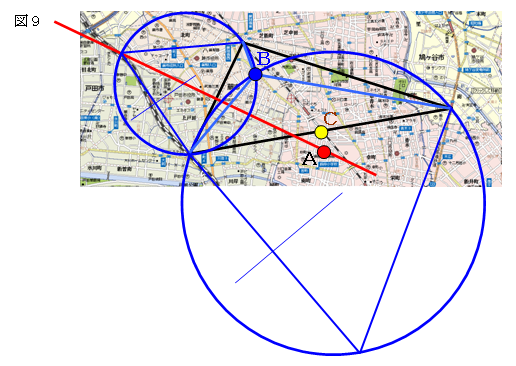
図9において、点A(物件A)は「3つの駅から等距離にある点」、
点B(物件B)は「3つの駅からの距離の和が最小な点」、
点C(物件C)は「3つの頂点までの距離の中で最長な距離が最小になる点」である。
物件Aは物件Cに比べて明らかに不便である。つまり「どの駅からも便利な場所」が、
3つの駅から等距離にある点とは一概にはいえないことがわかる。
次に物件Bと物件Cを比較してみると、最短シュタイナー問題の考え方では、距離の和が
最小だから、物件Bの場合は4.28km、物件Cの場合は、4.83kmにあり、物件Bの方がよいと
考えられるが、物件Bの場合、南鳩ヶ谷駅に行かなくてはならないときには、2.58kmも
歩かなければならないことになる。
その点物件Cは最大でも1.68km歩くだけですむのでよい、という考え方もあるのである。
つまり、「3つの頂点までの距離の中で最長な距離が最小になる点」を
考える場合もあるのである。
この点は鋭角三角形の場合は外心になるので、鈍角三角形の場合を考えてみる。
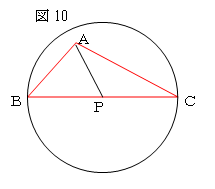
図10のように、∠BACが鈍角である鈍角三角形ABCにおい
て、BCを直径とする円を書き、その半径を r とする。円の中
心を点Pとすると、BP=CP=r となる。ここで、点P以外の点Q
では、BQかCQのどちらかが r よりも大きくなってしまう。
また、∠BACは鈍角であるから、PA≦r である。
よって、点Pは3つの頂点までの距離の中で最長な距離が r で最小になる点
であり、点P以外の点Qでは、AQ,BQ,CQのうち、どれかは必ず r より大きくなってしまうことがわかる。