バイオリンの音の振動について考察することで、三角関数のグラフに興味をもち、
単元の有用性を感じることが、この教材のねらいである。
まず、 y=sinx と y=cosx のグラフを、同じグラフ用紙に重ねて書き、
それぞれのグラフの対応する x の値における点の x 軸からの距離を測り、
符号に注意しながら、その距離を足した点をうっていってグラフをかくと、
合成した式である y=√2sin(x+(π/4)) になることが体験できる。
例えばバイオリンのある音の振動が y=11sinx+4cos2(x+(π/15)) で表せると
したとき、これを合成して式を求めることはできないが、グラフ用紙に y=11sinx と
y=4cos2(x+(π/15)) のグラフを重ねて書いて、 y=sinx と y=cosx のときと同じ
要領でグラフをかくと、この音の振動がどんな波形になっているかがわかっておもしろい。
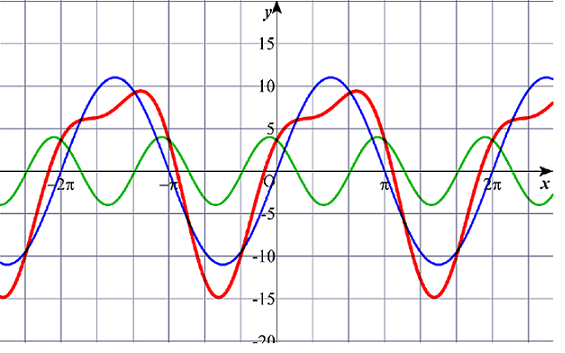
ちなみに、グラフは下図のようになる。青が y=11sinx 、緑が y=4cos2(x+(π/15)) 、
赤が y=11sinx+4cos2(x+(π/15)) のグラフである。
