架空の水陸両用観覧車のモデルを考え、観覧車の高さを正弦で表し、正の部分が空中、
負の部分が水中と考えることで、正弦の値の符号がイメージしやすくすることが、
この教材のねらいである。
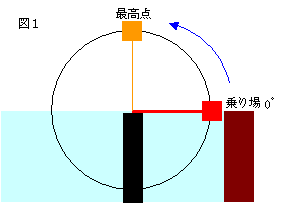
図1のような水陸両用の未来型観覧車がある。
乗り場は0°高さ0mのところで、初めは上にあがっていって空の景色を堪能し、180°のとこ
ろから水中に潜り、後半は水中で魚を見ることができるという、なんとも素敵な観覧車である。
この観覧車は同じ角速度で回転し、12分で1周する。
観覧車は出発から3分後に最も高い地点に到着するが、この観覧車がその半分の高さの
地点に着くのは、何分後だろうか?

何分後かを予想してみると、多くの人が素直に
3分の半分である、1分30秒後と答える。
しかし、図2を見て考えると、1:2:(√3)の
直角三角形を考えてもよいが、
sin30°=(1/2) であることから、
30°回転した時、すなわ3分÷3の1分後に半分
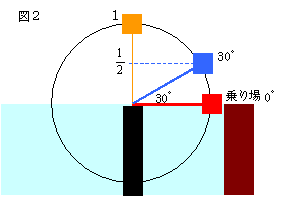
の高さの地点に到着することがわかる。
予想が多かった1分30分後には、45°回転して
いることから、sin45°=(1/√2) ≒0.7071より、
約70%の高さにまで上がっていることがわかる。
この図でいうと270°の地点から乗る、実際の
観覧車に乗ったときも、最初ゆっくり上がり、
途中一気に高度を上げて、また最高点付近でゆっくり上がることが体感できるはずである。
この後、回転させながらsin60°,sin90°,sin120°・・・と、観覧車の高さをイメージさせながら
値を求めていく。すると、sin180°=0となり、角度が180°を超えてからは、水中に潜って高さが
マイナスになることから、180°<θ<360°のとき、sinθの値が負になることがイメージし
やすくなる。