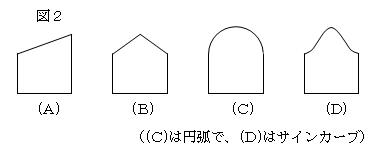
ワイシャツなどの袖の型紙の中に、正弦曲線(サインカーブ)があることがわかることから、
身のまわりに三角関数があることを実感し、単元の有用性を感じるのがこの教材のねらい
である。
ワイシャツの袖の型紙はどんな形になるだろうか?
この現実事象の問題を、次のようにモデル化して考える。
図1のように、円柱を斜めに切って、ABで縦に切り左右に開くと、図2の(A)~(D)の
どれになるだろうか?

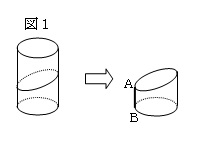
あらかじめサインカーブの切り口で切った紙を丸めて円柱を作ったものを見せて、開いて
見せる前にイメージさせて考える。
結果は(D)であるが、実際に予想させると、現在の単元が三角関数だから(D)だろうという
読みをしなければ、予想は(B)と(C)が多い。
検証方法は、さきほど見せた円柱を作ったものを開くのが一番簡単だが、ワイシャツやTシャツ
などの袖を実際に切ったり、大根を桂むきにしたり、ソーセージに紙を巻いて切ったりしても
よい。大根の桂むきは中村氏(2000)が授業実践を行っている。
また、逆に実際に紙で作った(A)から(D)の紙を丸めて円柱を作り、どの円柱が切り口が平面に
なっているかを見せるのも効果的である。
このしくみは、ワイシャツの型紙の他にも、雨どいの斜めのつなぎ目などにも見られる。
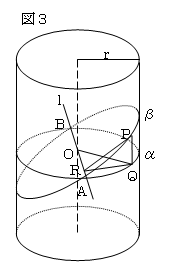
図3のように、円柱の半径をr、軸上の点Oを通って、軸に垂直な
平面をα、Oを通って軸とθ0の角をなす平面をβとする。
平面βで円柱を切ったときの切り口の曲線上の任意の点をPとし、
Pから平面αへ下ろした垂線の足をQ、Qからαとβの交線 l へ
垂線QRを引くと、PR⊥l より、∠PRQ=θ0だから、
QP=RQtanθ0 となる。また、交線 l と円柱の交点をA,Bとし、
∠AOQ=θとおくと、RQ=rsinθ となる。
したがって、QP=(rsinθ)tanθ0=(rtanθ0)sinθ となる。
切り口の曲線を平面に開くと、x=弧AQ=rθ,y=QP=(rtanθ0)sinθ が点Pの座標と
考えることができるから、点Pの軌跡は、y=(rtanθ0)sin(1/r)x となる。
例えば、r=1, θ0=45°のときは、y=sinx である。
切る角度θ0は振幅だけに影響し、円柱の半径rは振幅と周期を変えることがわかる。
一般的な証明は難しいので、簡単にしたい場合は、r=1, θ0=45°の場合だけ扱うとよい。