平面図形のパズル的な課題を解決することで、軌跡と領域という概念のイメージを深める
ことが、この教材のねらいである。
点Aと点Bを与え、次のような軌跡や領域を作図することを考える。

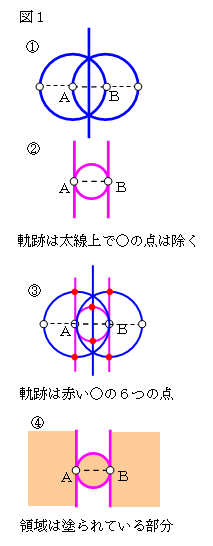
点Cの軌跡は図1の①の青色の太線部分となる。
AC=BCになるときは、線分ABの垂直二等分線上、
AB=ACになるときは、点Aが中心でABを半径とする円上、
AB=BCになるときは、点Bが中心でABを半径とする円上、
に点Cはそれぞれある。
点Cの軌跡は図1の②の桃色の太線部分となる。
∠A=90°になるときは、点Aを通りABに垂直な直線上、
∠B=90°になるときは、点Bを通りABに垂直な直線上、
∠C=90°になるときは、ABを直径とする円上、
に点Cはそれぞれある。
点Cの軌跡は図1の③の赤色の6つの点となる。これらの
点は①と②の軌跡、つまり青色線と桃色線の交点である。
点Cの領域は図1の④のベージュ色に塗られている部分となる。
これは、②の図を基にして塗ったものである。