三角比が生まれた歴史を通して、三角比に興味をもつことが、この教材のねらいである。

ギリシャのトレミー(プトレマイオス)は
紀元後150年に著書「アルマゲスト」で、
弦の計算の仕方と、0.5°おきの詳しい
弦の表を掲げている。
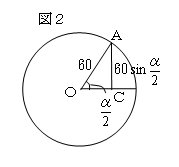
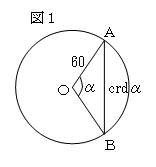
これによるとトレミーは、図1のように
半径 60 の円の中心角 α の弦をcrdα とし、その値を測って右のように表にまとめている。
| 中心角α | 弦AB(crdα) |
|---|---|
| 1° | 1;02,50 |
| 2° | 2;05,40 |
| 3° | 3;08,28 |
| 4° | 4;11,16 |
| 5° | 5;14,04 |
| : | : |
この時代は60進法が使われていたため、弦ABに表されている数字
は60進法である。また半径が 60 なのも、60進法だからであると
いわれている。例えば、crd4°=4;11.16であるが、これは、
crd4°=4+11/60+16/602=4+0.1833+0.0044=4.1877 ということ
である。この表を現在の三角比表と比べてみると、図2のように、
crdα は半径 60 で角度 α/2 のときのACの2倍になるので、crdα=120sin(α/2)になる。
例えば、crd4°=120sin2°=120×0.0349=4.1879 となり、ほぼ一致することがわかる。
また、円の弦の長さを表にしていったことから正弦という名前がついたと考えられる。
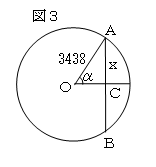
インドのアリアバータは、510年頃に図3のように半径を3438とした円
の半弦の表(現在の正弦表)をつくり、右下のような表にまとめた。
円の半径を3438にしたのは、円周の長さ2πr(rは半径)を360×60とした
ところから、r =360×60/2π≒3438(当時はπ≒3.1416として計算した)
として算出したようである。
| 角度 α | 正弦 x |
|---|---|
| 0° | 0 |
| 15° | 890 |
| 30° | 1719 |
| 45° | 2431 |
| 60° | 2978 |
| 75° | 3321 |
| 90° | 3438 |
| : | : |
例えば、右表から、α=30°のとき、x=1719/3438=0.5
α=45°のとき、x=2431/3438=0.707097…
α=60°のとき、x=2978/3438=0.866201… となり、
現在の三角比表のsin45°=0.7071,sin60°=0.8660 と比べ、小数第3位
までの精度で正しい値を示している。
また、アリアバータは図の弦ABを猟師の弓の弦という意味で jiva と呼んで
いたが、これを後にアラビア人が同じ発音の言葉で入江とか谷間という意味の jaib と訳し、
それをラテン語に訳されるとき入江とか谷間という意味の sinus に代えられ、今の英語の sine
になったといわれている。辺の比として正弦を定義したのは、ドイツのラエティックス(1551年)、
正弦に対する最初の略号 sinA を用いたのはフランスのジラール(1624年)といわれている。
正弦が弧の弦として考えられている段階では余弦はそう必要なものではなかったが、直角三角
形が基本図形として捉えるようになってくると、余角の正弦としての余弦の必要性がでてきた。
余弦は、イタリアのプラトーが1120年頃に残りの弦という意味で chorda residui と呼び、
イギリスのガンター(1620 年)が、co.sinus と書いている。現在の略号 cosA を用いたのは
イギリスのムーア(1674年)である。
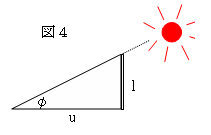
実用的な余接の表を最初に作ったのは、アラビアの
アル・バッタニ(920年)で、図4のような水平な影の長さで
u =l×(cosφ/sinφ)の値である余接の表を1°ごとに作った。
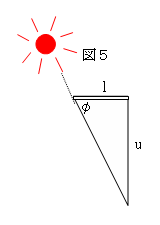
最初の正接の表を作ったのは、アラビアのアブール・ワファ(980年)で、
図5のような垂直の影の長さで、u =l×(sinφ/cosφ)の値である正接の
表を15′ごとにつくった。tangentという用語を用いたのは、デンマーク
のトーマス・フィンケ(1583年)である。