円周率を正確に求めていった歴史を通して、三角比に興味をもち、単元の有用性を感じること
や、具体例を通して様々な見方考え方を体験することが、この教材のねらいである。

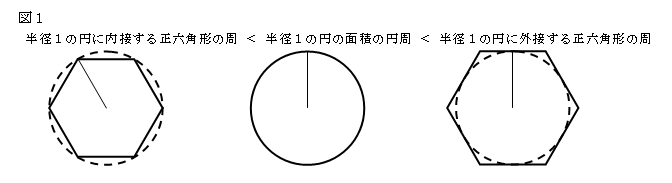
図1のように、半径1の円に内接する正六角形と外接する正六角形を考える。すると、円周の
長さは内接正六角形の周の長さより長く、外接正六角形の周の長さより短いと考えられる。
内接正六角形の周の長さは、2×sin30°×6=6で、半径1の円周の長さは2π、
外接正六角形の周の長さは、2×tan30°×6=4√3なので、
6<2π<4√3 より、3<π<2√3。√3=1.73とすると、3<π<3.46であること
がわかる。
この角の数を増やしていくと、内接正多角形の周の長さも、外接正多角形の周の長さも、
ともに円周の長さに近づいていく。
例えば正六角形を正180角形にすると、2×sin1°×180=2×0.017452…×180≒6.2828
2×tan1°×180=2×0.017455…×180≒6.2838なので、6.2828<2π<6.2838 より、
3.1414<π<3.1419であることがわかる。
※三角比の値は関数電卓を使って教科書の三角比の表よりも詳しく求めた。
歴史的には、紀元前3世紀ごろにアルキメデス(ギリシャ)が、正6角形から始めて、
正12角形→正24角形→正48角形→正96角形と角の数を増やしていき、角の数を増やしていく
と、辺の和は円周の長さに限りなく近づいていくことから、最終的には正96角形を利用して、
3+(10/71)<π<3+(1/7)、すなわち3.1408…<π<3.1429…であると計算した。
これは、まだ小数第2位までの近似(3.14まで)である。
以後の学者はこの手法を使ってπの計算競争に次々と名乗りをあげ、1610年にルドルフ(ド
イツ)が、この方法では計算の限界であるといわれている、正262角形を使い、小数第35位まで
の近似に成功した。ちなみに、262は19桁の数で、約50京である。(京は兆の1000倍の単位)
円周の長さで比較するより、「円の面積は内接正六角形の面積より大きく、外接正六角形の
面積より小さい」という比較の方が大小関係は明瞭でわかりやすいし、多角形の面積を求める
教材にもなる。よって、面積の場合も考えてみる。
内接正六角形の面積は、(1/2)×1×1×sin2°×6=(3√3)/2で、半径1の円の面積は π、
外接正六角形の面積は、(1/2)×2tan1°×1×6=4√3なので、
(3/2)√3<π<2√3。√3=1.73とすると、2.59<π<3.46となる。
これは円周のときに比べ、下限があまり近似していないことがわかる。
この角の数を増やしていくと、内接正多角形の面積も、外接正多角形の面積も、
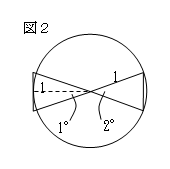
ともに円の面積に近づいていく。正六角形を正180角形にすると、
図2より半径1の円の内接180角形の面積と外接180角形の面積は
それぞれ
(1/2)×1×1×sin2°×180=0.034899…×90≒3.1409
(1/2)×2tan1°×1×180=0.017455…×180≒3.1419より、
3.1409<π<3.1419となる。
円周で近似したときに比べ、近似するイメージはしやすいが、近似の速度は遅い。