無理数が誕生した歴史の話を通して単元に興味をもち、無理数の作図を通して
無理数が数直線上にとれることを体感することが、この教材のねらいである。
古代ギリシャ人は、直線について次のように考えていたといわれている。
『世の中には究極の単位の「点」(最小だが大きさがある)があり、それがつながって直線となる。
その線を顕微鏡で見ていくと、きっとツブツブの点が数珠つなぎにたくさん並んでおり、
いくつあるかも数えられるはず。そして、その「数の違いが長さの違い」である。』
しかし、すぐにこの考えは「無理数」という存在によって見事に否定されてしまった。
「無理数」の存在でおきた矛盾とは、『世の中に「究極のツブ」があるのなら、そのツブの
数の比が長さになる。つまり2本の線分の比は常に「自然数:自然数」となるはずである。
しかし、無理数は「自然数の比」では表わせない。』ということである。
例えば、長さ1cmの中にある「究極のツブ」の個数をn個とすると、長さ3cm(整数)の中のツブ
の個数は3n個、比で表わすと1:3となる。長さ3.5cmつまり(7/2)cm(有理数)の場合は、ツブ
の個数は(7/2)n個になるが、ツブは究極に小さいツブにできるので、nを2の倍数にすると、
(7/2)nも自然数となり、比も自然数の比となる。
しかし、長さ√2cm(無理数)の場合は、底辺と高さが1cmで底角45°の直角三角形の斜辺
の長さなので、ツブを並べて表せるはずだが、この場合ツブの個数は√2n個と無理数となり、
√2nはnをいくつにしても自然数とならないため、矛盾が生じたのである。
当時、三平方の定理を見つけたピタゴラス派では、この矛盾を見つけてからは、
無理数は「あってはならない数」とされ、絶対に他言は無用としたのだが、
それを外部にもらしたために仲間内で処刑されたものまでいたといわれている。
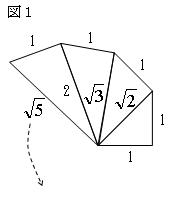
図1のように、底辺が√(n-1)、高さ1の直角三角形から、無理数√nの長さ
を次々と作図し、無理数が数直線上にとれることを実感する。

正確に作図するにはコンパスを使う必要があるが、
直角が測れる定規だけでの作図でも十分である。