光行差の現象について

更新したのでCtrlコントロールキーを押しながらＦ５を押してください

　

　光行差の現象は、皆さんよくご存じかと思いますが、星を観測するとき、望遠鏡を実際にある星の方向に向けても見えない現象ですね。地球は宇宙空間を動いているため、実際の方向とは若干ズレた方向に望遠鏡を向けなければならないことです。

　これを発見したのはイギリスのジェームス・ブラッドリー（１６９３〜１７６２）という人で、もう２００年以上前のこと１７２７年です。どのくらい望遠鏡を傾けなければいけないかの角度の計算式もブラッドリーの式として知られています。

　sinβ＝（ｖ／ｃ）sinα

という式ですが（次のＦｉｇ．１参照）、これを特殊相対性理論ではどのようにして説明しているのか、

また（ｃ−ｖcosθ ）による相対的光速度説（仮称）では、どのようにして証明するのかを、以下簡単に解説しましょう。

　

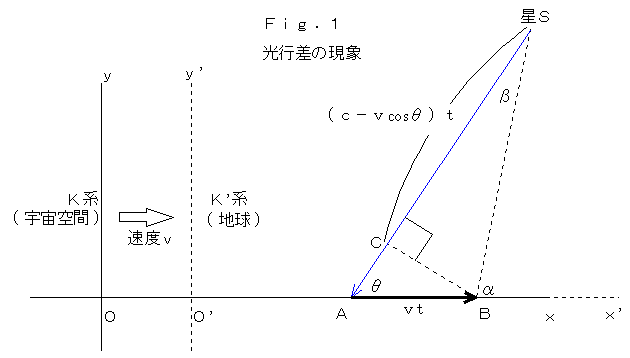
　初めに特殊相対性理論ではどのように計算しているのかを、多くの相対論の教科書に書かれているものを紹介します。

　「われわれの特殊相対性理論によってブラッドリーの式を証明してみよう。アインシュタインの光速度不変の原理によって光速度は Ｋ 系も Ｋ’ 系も一定値 ｃ である。よって次の式が成り立つ。ただし ｚ 軸は考えないとする。

ｖ＝ｄｘ／ｄｔ＝ｃ・cosθ

ｖ’＝ｄｘ’／ｄｔ’＝ｃ・cosα

ｄｙ／ｄｔ＝ｃ・sinθ

ｄｙ’／ｄｔ’＝ｃ・sinα

　これらの式から、アインシュタインの速度の加法則によれば次式を得る。

　

ｃ・cosθ＝（ｖ＋ｃ・cosα）／｛１＋（ｖ／ｃ）cosα｝

ｃ・sinθ＝（ｃ・sinα）／｛１＋（ｖ／ｃ）cosα｝

　逆に解いて

cosα＝｛cosθ−（ｖ／ｃ）｝／｛１−（ｖ／ｃ）cosθ｝

sinα＝｛sinθ｝／ ｛１−（ｖ／ｃ）cosθ｝

　したがって光行差角βは

sinβ＝sin（α−θ）＝sinαcosθ−cosαsinθ

　　 ＝｛sinθcosθ−sinθcosθ＋（ｖ／ｃ）sinθ｝／｛１−（ｖ／ｃ）cosθ｝

　ここで、地球の運動は小さいから、ローレンツ因子は無視して捨てれば、

sinβ＝（ｖ／ｃ）sinθ／｛１−（ｖ／ｃ）cosθ｝ となる。

　一方、

sinα＝｛sinθ｝／ ｛１−（ｖ／ｃ）cosθ｝であるが、これも地球の運動は小さいから、ローレンツ因子は

無視して捨てる。

　そうすれば、

sinβ＝（ｖ／ｃ）sinα

となり、ブラッドリーの得た式と一致する。特殊相対性理論は光行差の現象を見事に証明する。アインシュタインの速度の加法則と光速度不変の原理は正しいことが証明された」

というものです。

　こういう「追っかけ近似解」（結果が分かっているので、それに向かって項を捨てながら近似的に求める方法）は相対性理論ではよく見かける計算法です。

　

　私はこういう近似計算をしません。純粋に理論的な計算をしてみましょう。

　宇宙空間Ｋ系での光速は ｃ です。この光は運動系地球 Ｋ’ 系では（ｃ−ｖcosθ ）です。

上図Ｆｉｇ．１のΔＡＢＣにおいて、

ＢＣ＝（ｃ−ｖcosθ）ｔ・tanβ＝ｖｔ・sinθ

ですから、

ｃ−ｖcosθ＝ｖsinθ／tanβ＝ｖcosβsinθ／sinβ

となり、両辺にsinβを掛けて整理すれば、

ｃsinβ＝ｖcosβsinθ＋ｖcosθsinβ＝ｖsin（β＋θ）

　　　 ＝ｖsin（π−∠ＡＢＳ）＝ｖsinα

したがって

sinβ＝（ｖ／ｃ）sinα

となり、ブラッドリーの式が得られます。

　

　以上の相対的光速度（ｃ−ｖcosθ ）による計算は現在のところ、公的に（学界で）認められているものではありません。

また拙著以外の書籍には一切掲載されてはいません。

　ところが、小生に無断で上記理論展開をそのままコピーして、運動系の光速度 ｃ’ を測定した論文を見たことがあります（論文のタイトルや執筆グループもすべて分かっていますが、ここでは公表しません。なぜか未成年者だからです）。参考文献の項に小生の名前も理論展開のことも一切書いてはいませんでした。アインシュタインがポアンカレの論文を盗作したのと同じです。

　使っても構いませんから、出典として明記しておいてください。

（２００１年２月２７日／２０１６年９月４日記／窪田登司）

目次のあるトップページは　こちら　　　　

お問い合わせ、ご質問などは手紙またはメール　kubota-takashi@outlook.jp　 まで

　

以下は芝浦工業大学学長 村上雅人教授から頂戴した光行差の現象に関する論説です。

　

ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー

　

Bradleyの光行差aberration　　　　　　　 芝浦工業大学 村上雅人

　　　　　　　　　　　　　　　　　　

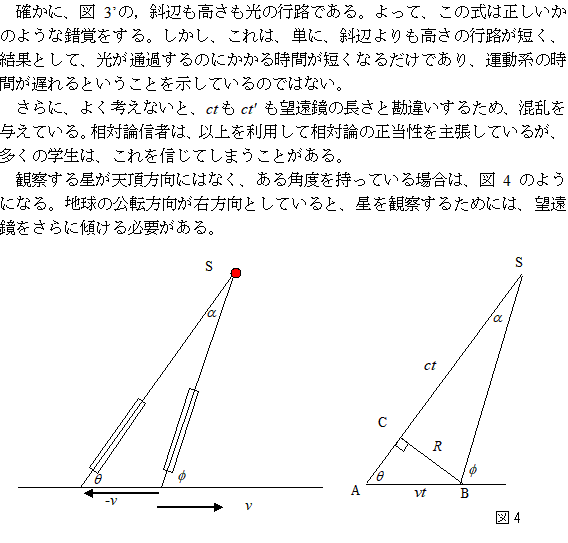
観察する星が天頂方向 (zenith) にある場合

　

地球が静止しているとすると、

望遠鏡をまっすぐ上に向ければ、星を観察することができる。

しかし、実際には、この方向に星を観察できない。

理由は、地球が公転しているためである（Bradleyの発見）。

　

　地球が、速度vで右方向に動いているとすると、ずれ角aが生じ、

星からの光は、地球の運動とは逆方向にずれる。

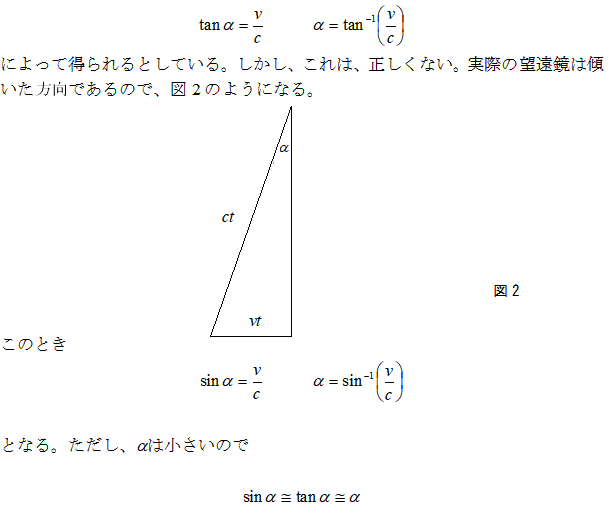
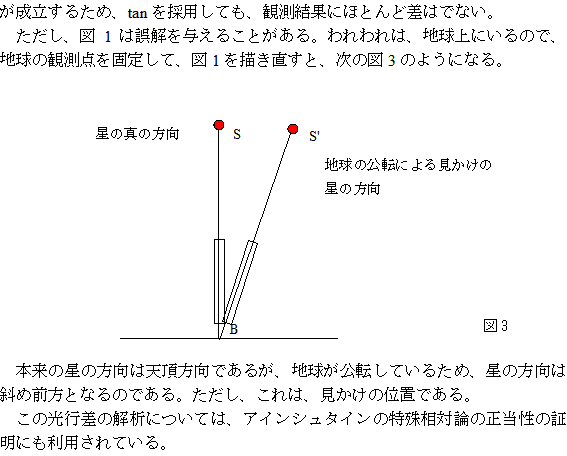
　そして、多くの文献では、図1から角度aは
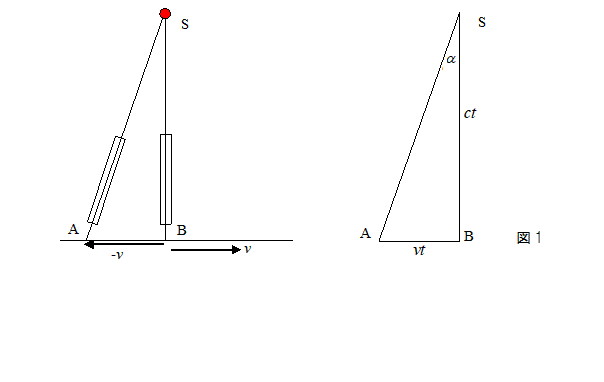