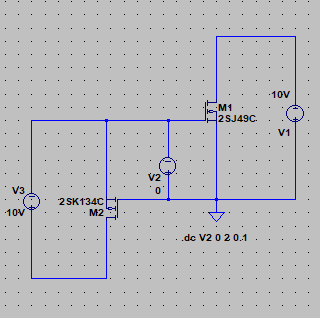
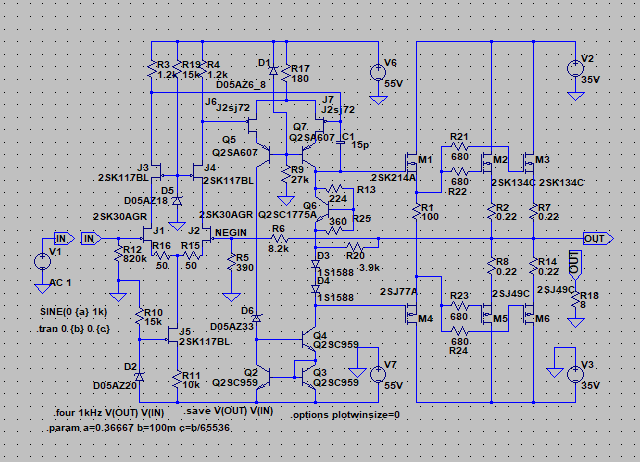
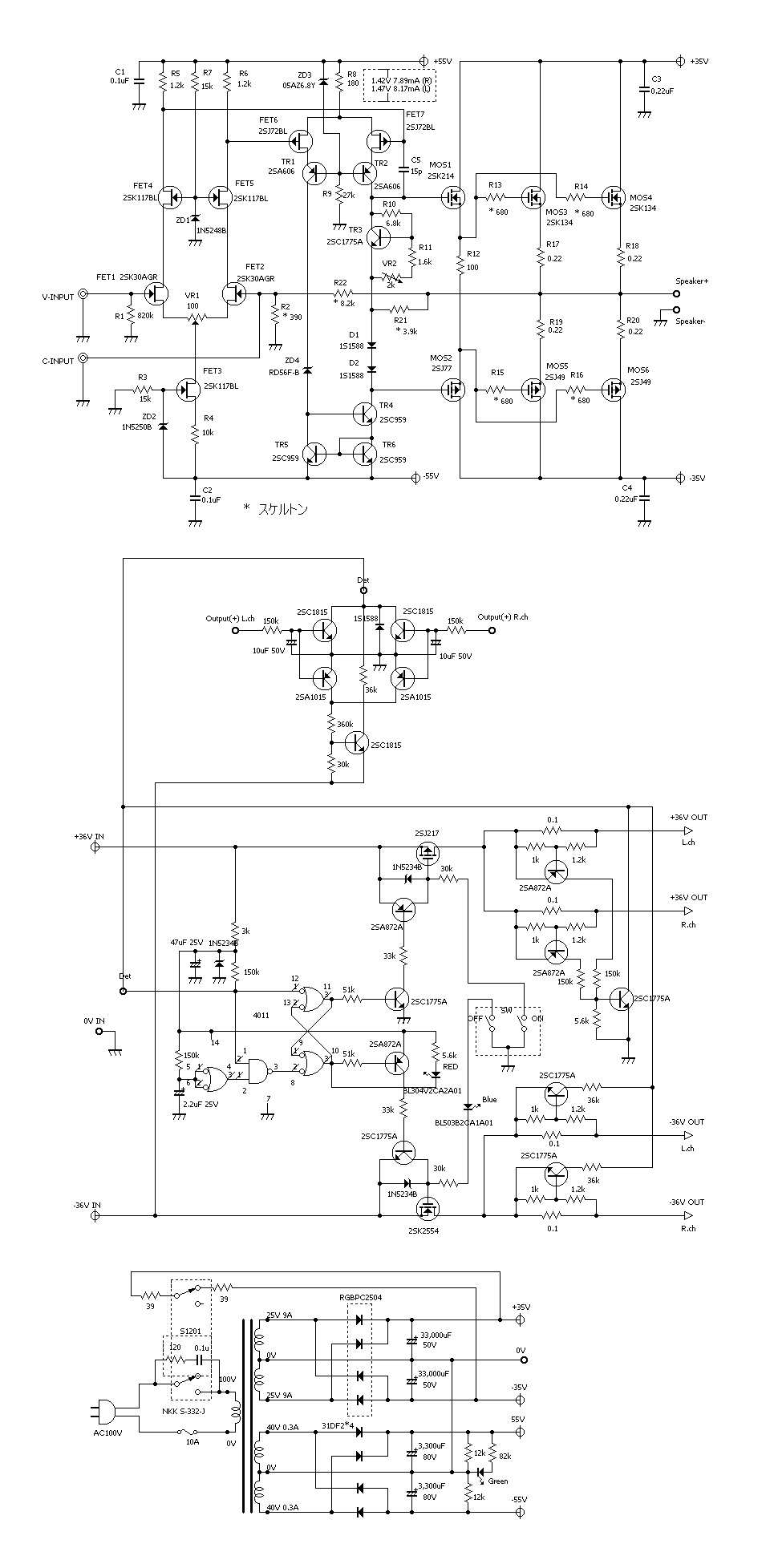
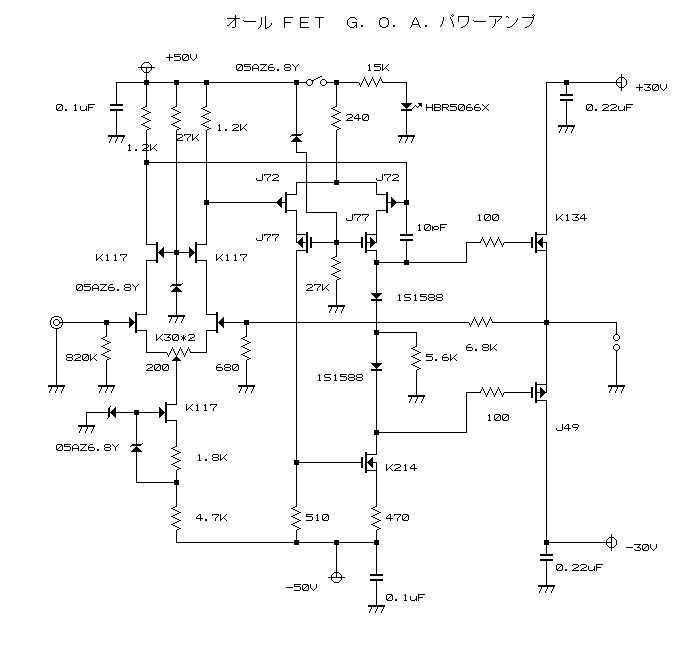
| �E���������B �E�̂ɁA10�N�O�ɍ�����E���I�[���e�d�s�@�f�n�`�p���[�A���v�����ς̎d�V�ƂȂ����B �E����Ȋ������������̂��A |
|
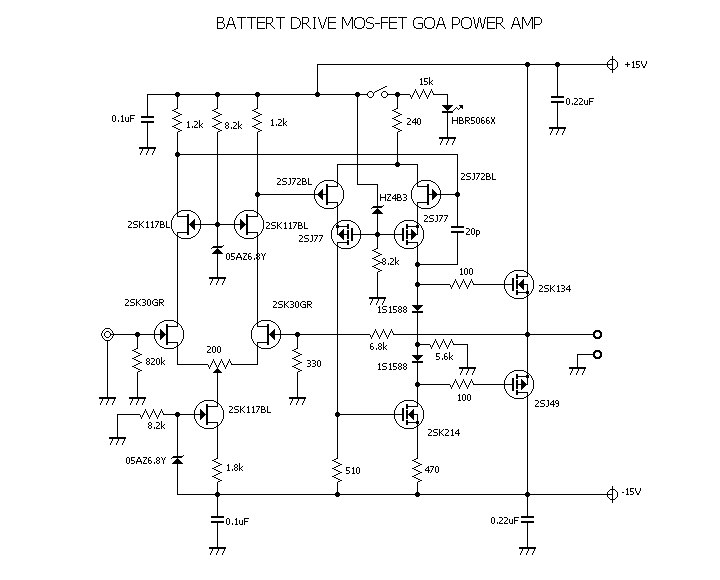
 |
|
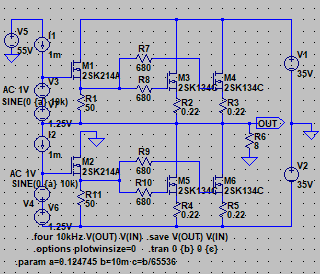
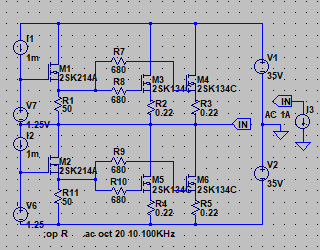
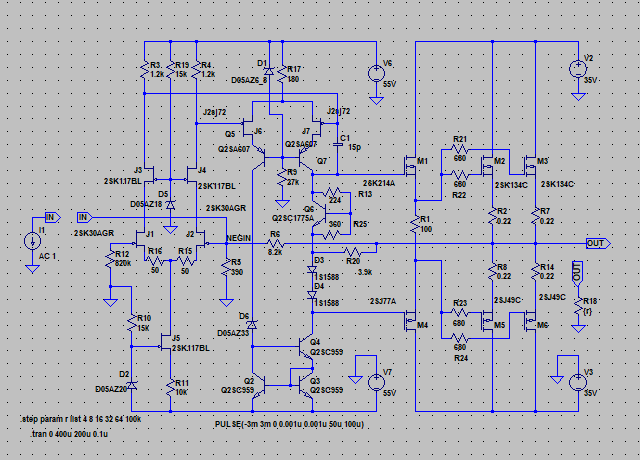
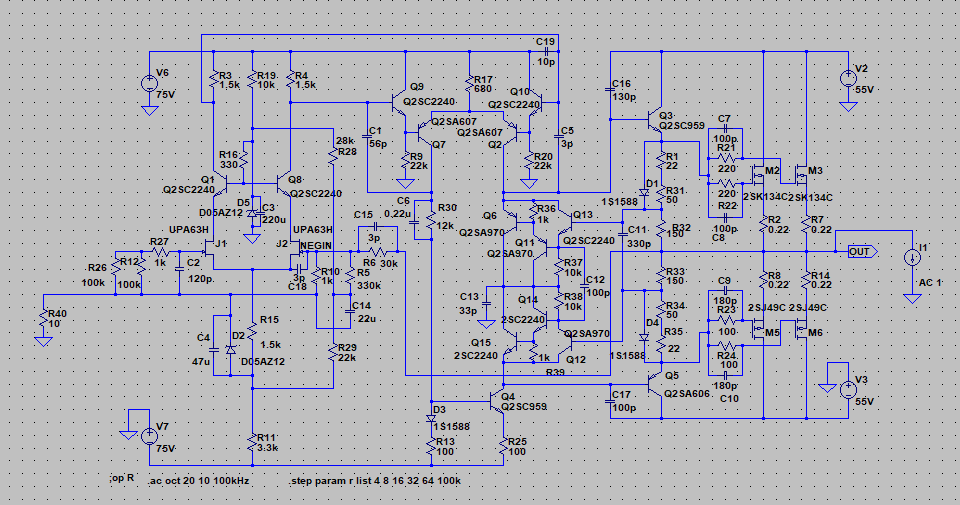
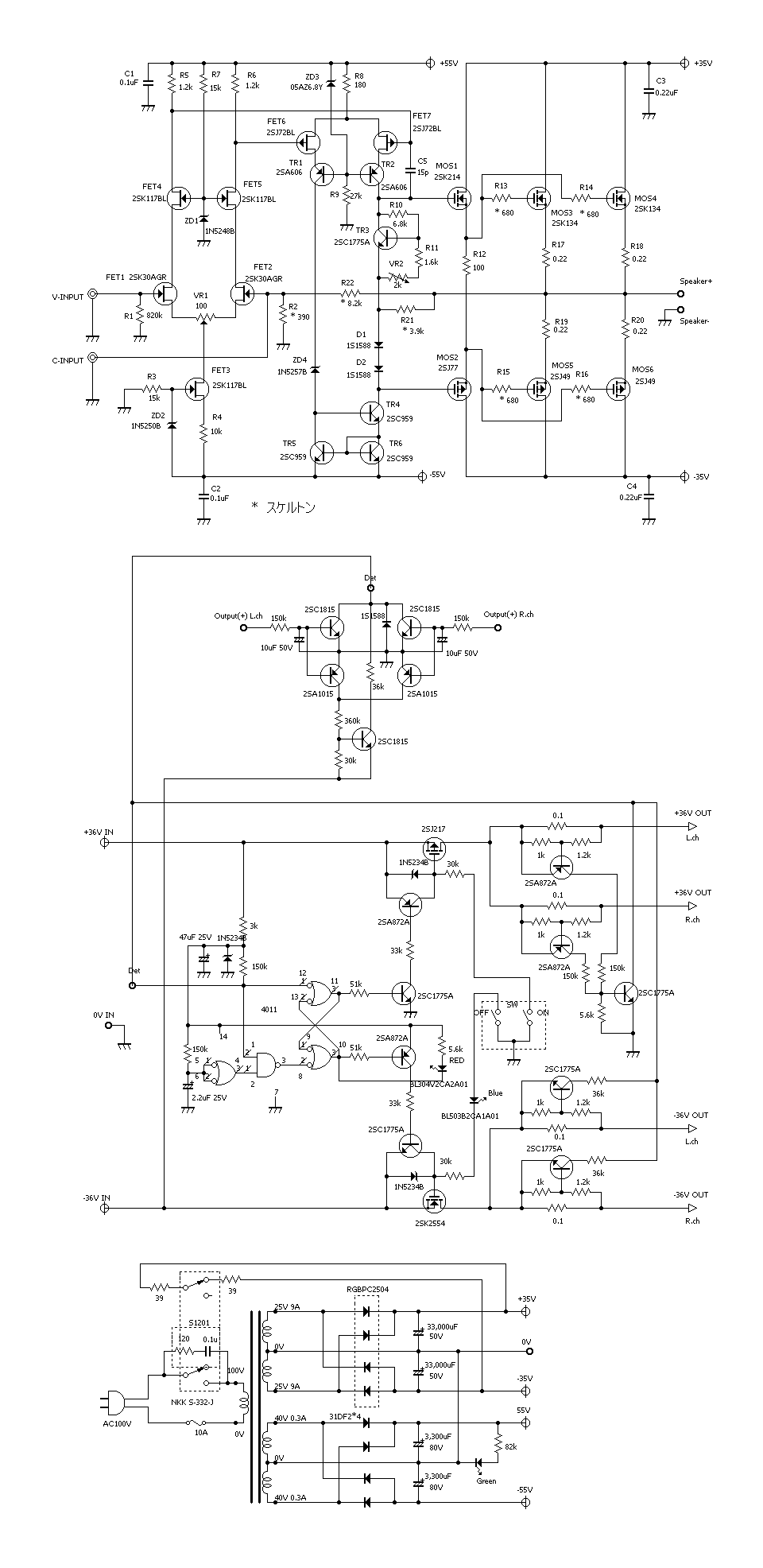
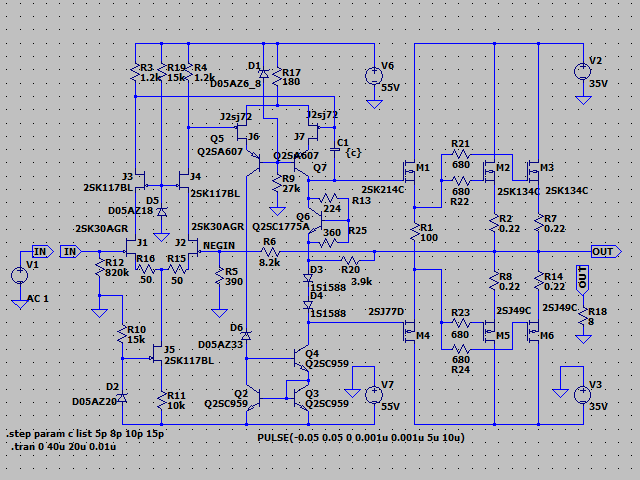
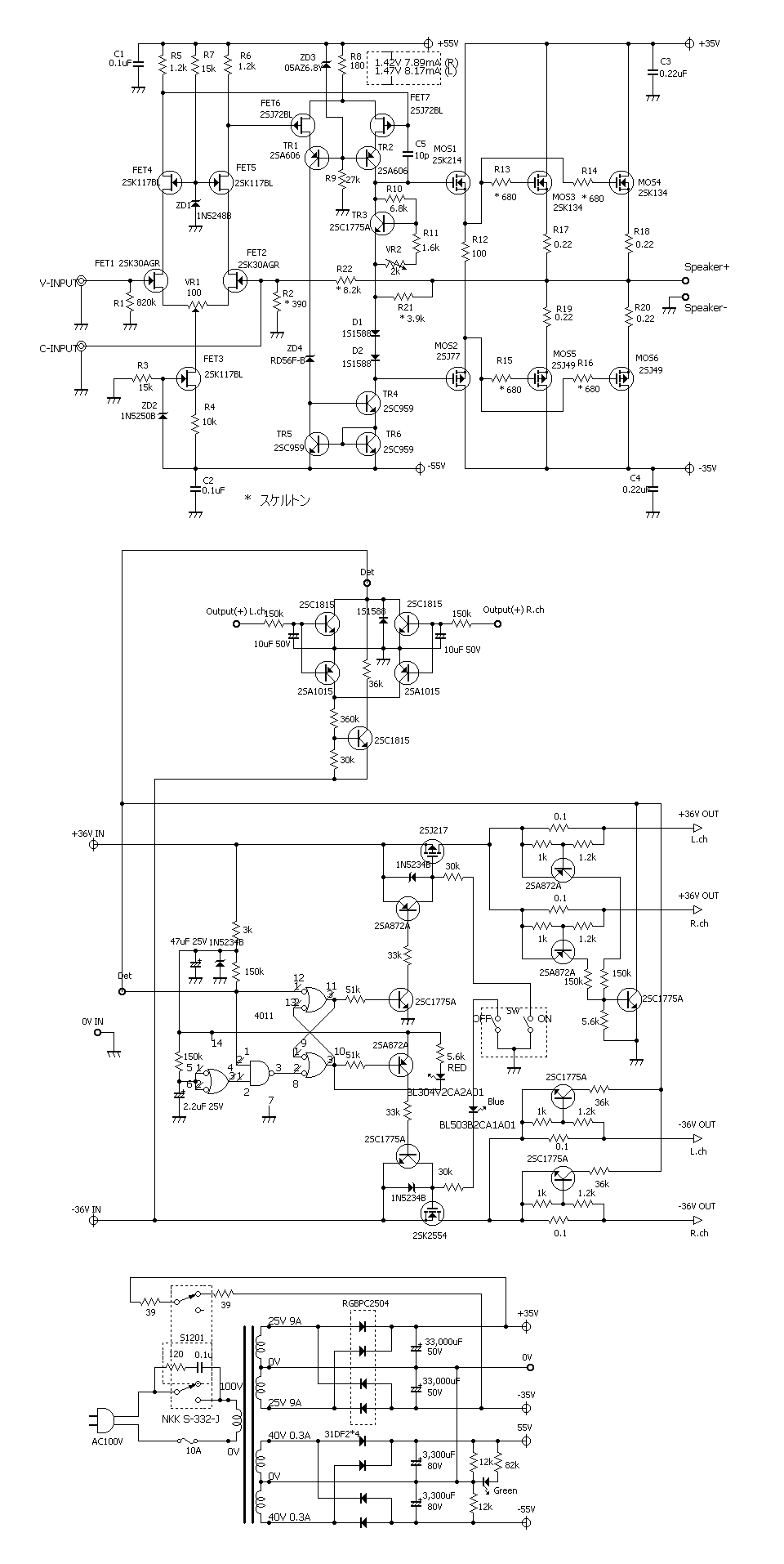
| �E����Ȋ����ɁB �E�w�Ǖς���Ă��Ȃ��B�i���j �E���A�d���d�����}�P�T�u�ɕύX���A����ɍ��킹�Ē�d����H���̃c�F�i�[�_�C�I�[�h�ɗ����d�����K�肷���R�̒�R�l�����A�Q�i�ڍ����A���v�̃J�X�R�[�h��H�̌Œ�d����K�v�Œ���Ƃ��A�S�d���d�l����Q�d���d�l�ɕύX���A���킹�Ă��̍ۃN���[�Y�h�Q�C���ݒ���ŋߐ��삵���䂪���c�d�r�����S�Ώ̌^��o�b�e���[�h���C�u�s���S�Ώ̌^�p���[�A���v�Ɠ����Q�Q�{�ɏグ���B �E�v������`�E���C�I���o�b�e���[�d���d�l�ɂ��āA���`�E���C�I���Œ������B�Ƃ�����|�B |
|
 |
|
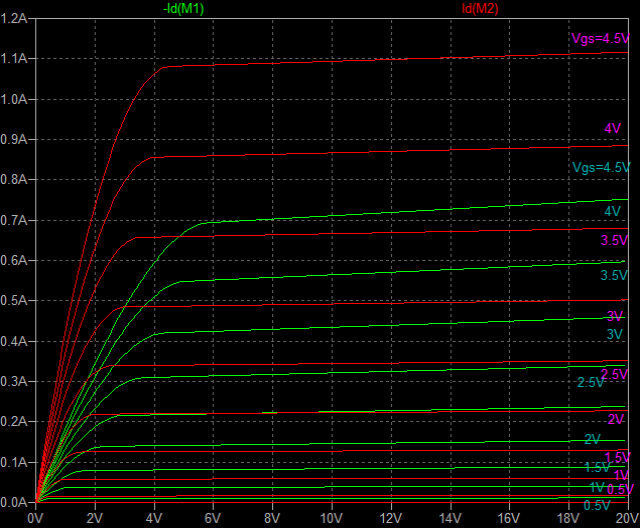
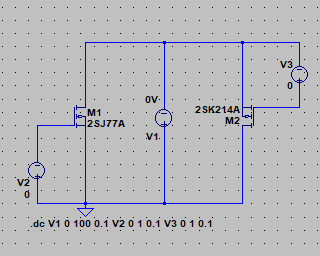
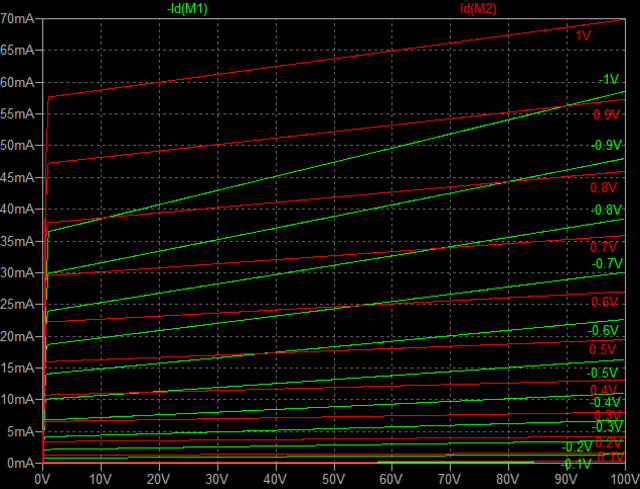
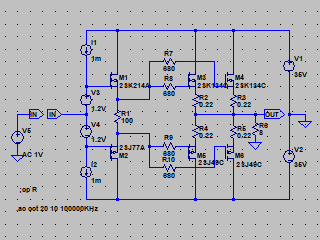
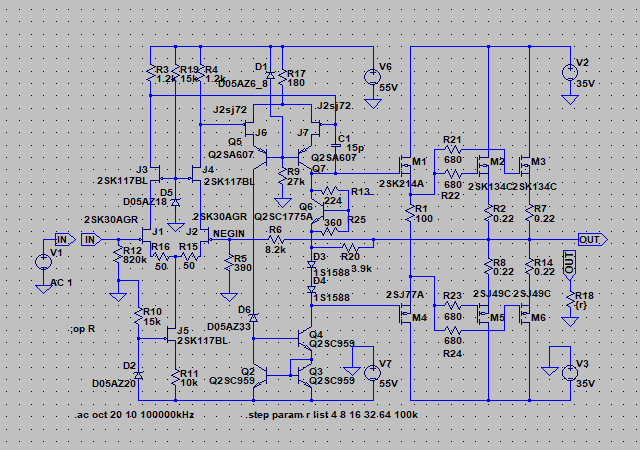
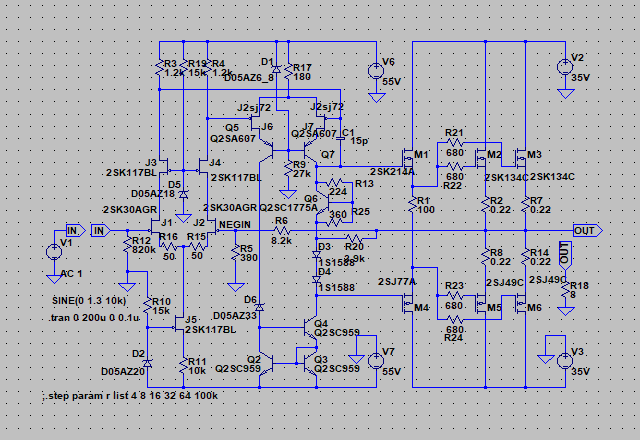
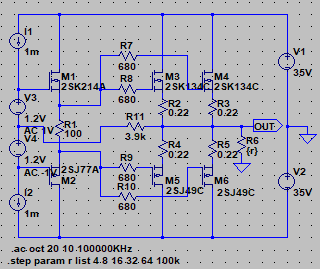
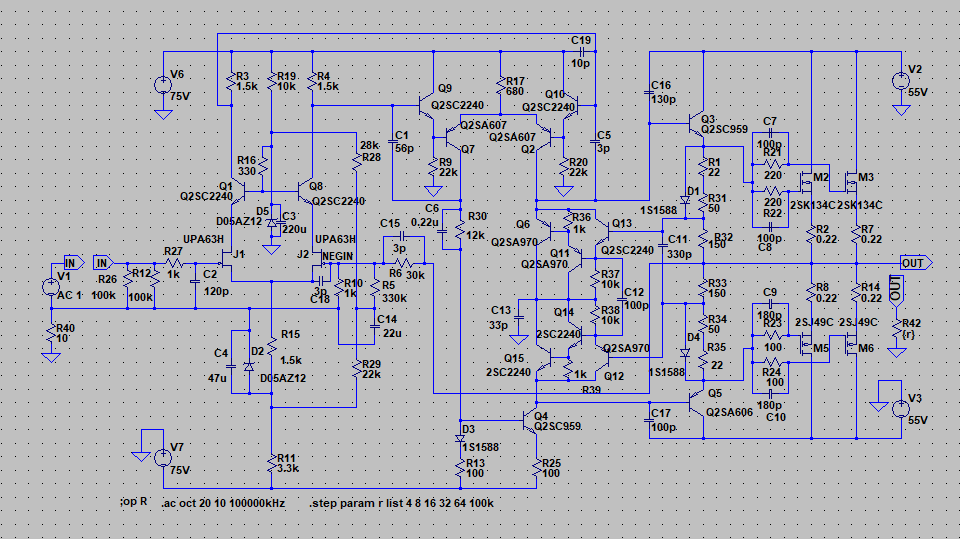
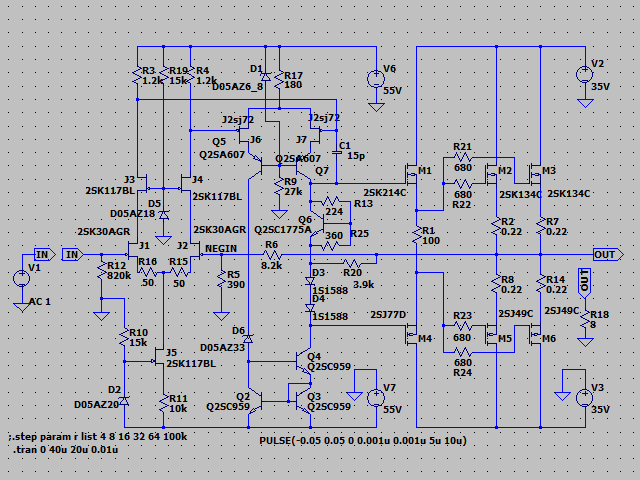
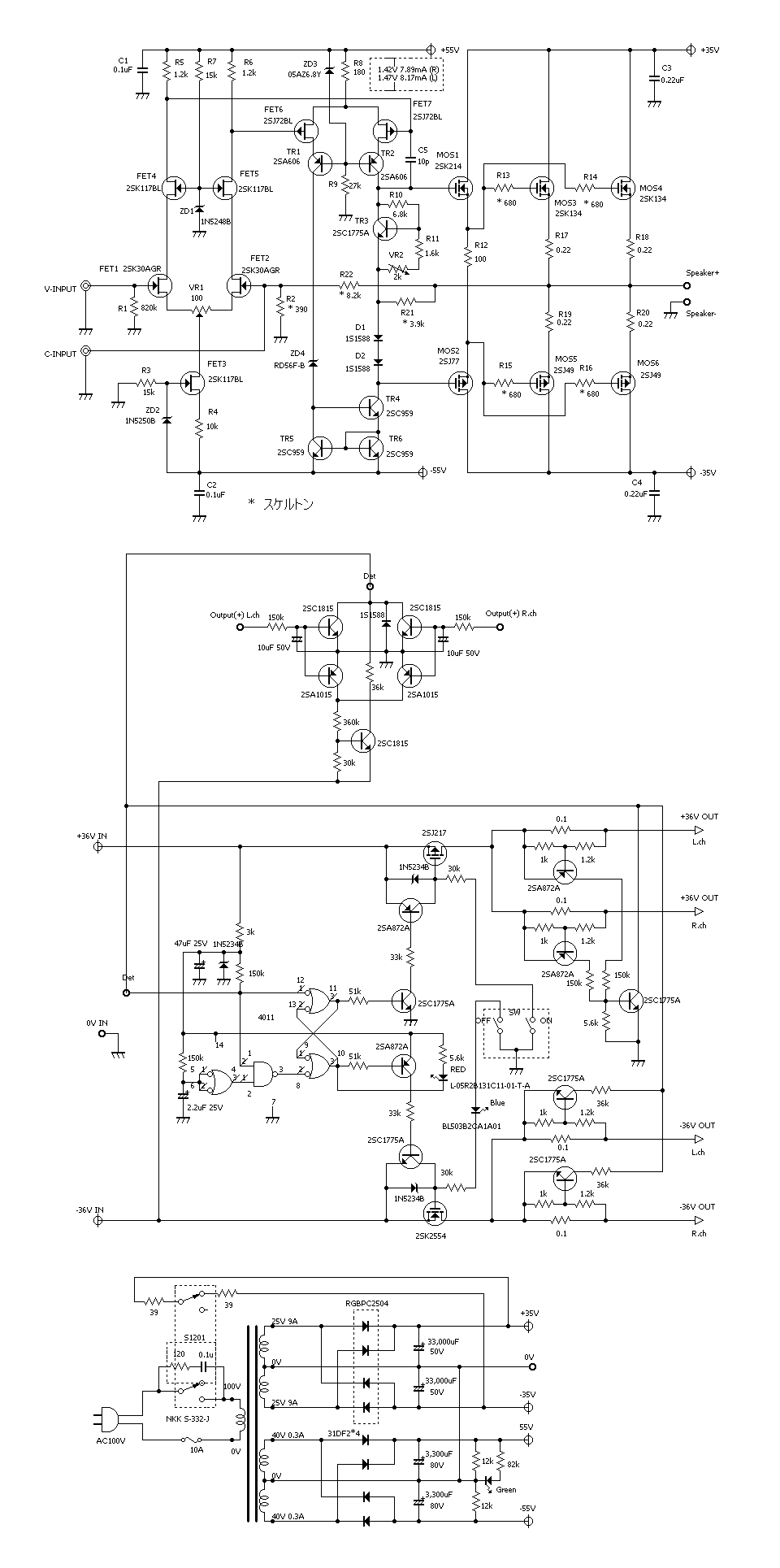
| �E�܂��A�ǂ���ɂ��Ă���H�I�ɂ͂l�i�P�X�X�Q�N�P�Q�����̂m���|�P�R�V�A�I�[���e�d�s
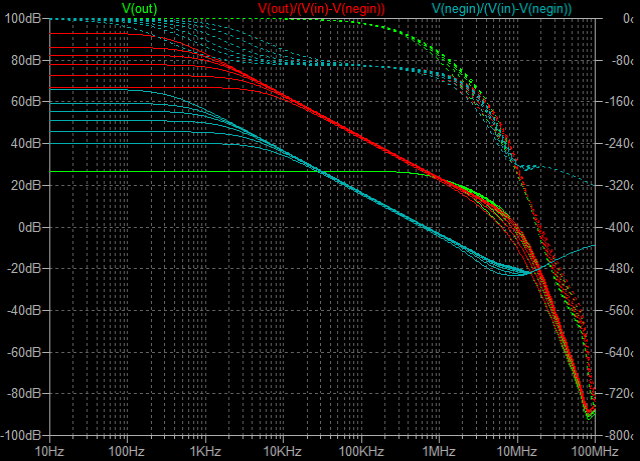
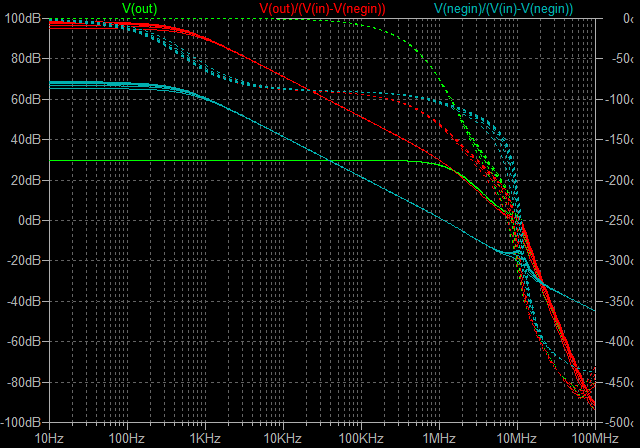
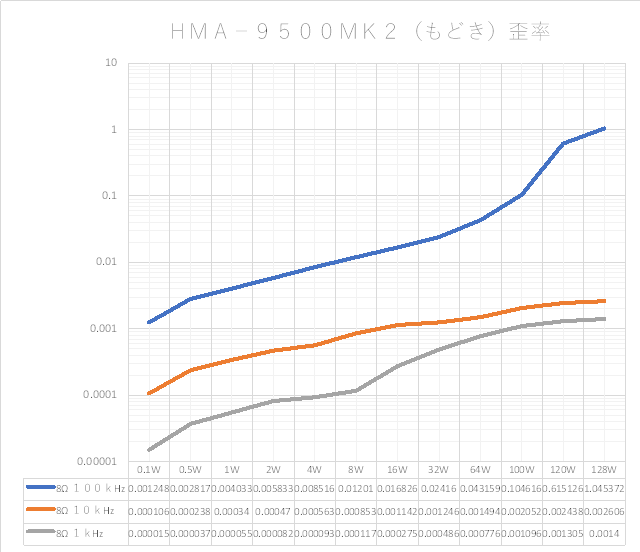
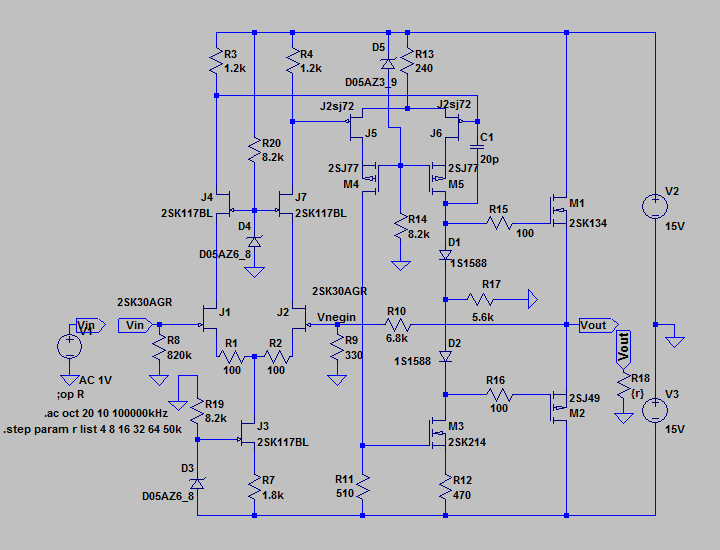
3cH�p���[�A���v�ɂ����߂��f�n�`�p���[�A���v�ł���B �E�ŁA���̏�Ԃɂ����闘�����ʑ��|���g���������k�s�r���������ŊςĂ����B �E���ׂ̂q�P�W���S���A�W���A�P�U���A�R�Q���A�U�S���A�T�O�����i���׃I�[�v�������j�̏ꍇ�̃p�����g���b�N��́B |
|
 |
|
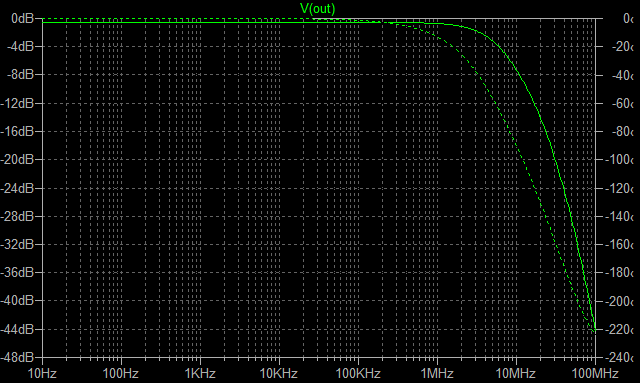
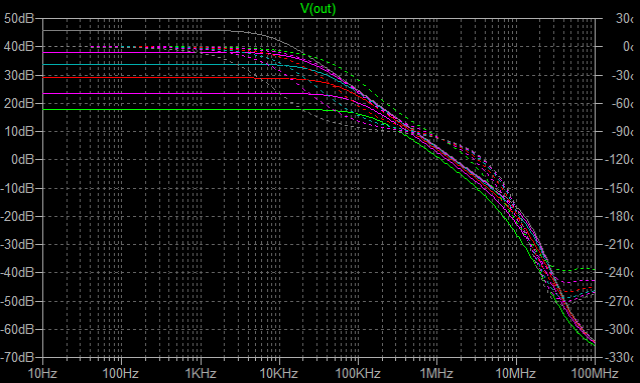
| �EGOA�ł��邩��A�I�[�v���Q�C���i�ԁj�͕��ׂɂ�����炸���łP�O��Hz�t�߂܂łقڈ��ŁA�T�R��B�}�Q��B���x�ł���B �E�N���[�Y�h�Q�C���i�j�͋A�҉�H�Őݒ肵���ʂ�łQ�U�D�V��B�i����Q�Q�{�j�B���������ă��[�v�Q�C���i�j�����ׂɂ�����炸���łP�O��Hz�t�߂܂łقڈ��ŁA�Q�V��B�}�Q��B���x�B �E�ƁA���ɂ͓��Ɍ����ׂ����Ƃ͂Ȃ����A������_���g�����S�O�O��H���`�T�O�O��Hz���x�ƁA���O�ɒႢ�̂��ӊO�ȂƂ���ł͂���B |
|
 |
|
| �@�@ | |
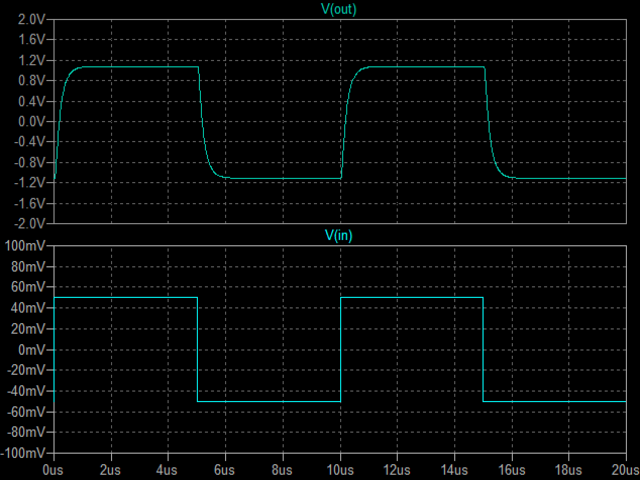
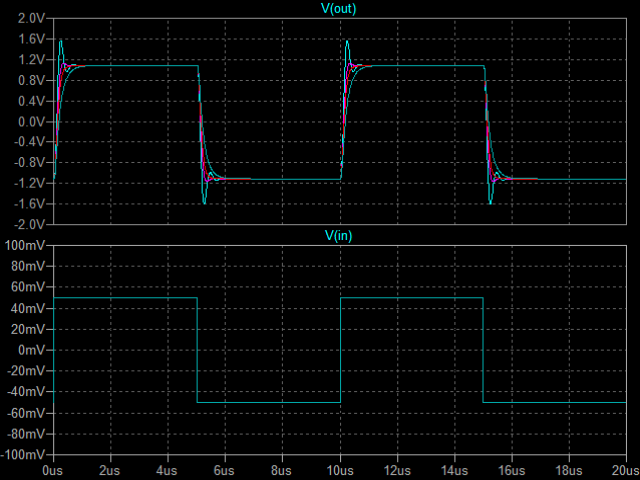
| �E�Q�i��G-D�Ԃ̈ʑ��C�́A���`�g�����������]�O�̂P�O��F���Q�O���e�ɕς����B �E���̊ώ@�����̎ʐ^�������A���ɏォ��A�ʑ��C���P�O��F�A�Q�O��F�A�����ĂR�X��F�̏ꍇ�ŁA�����P�O��Hz���`�g�����ʼnE���P�O�O��Hz���`�g�����B �E�ʐ^�͂Q���ۂʼn������͔g�`�ŏオ�o�͉����g�`�B���̏ꍇ�A�S�Ė����ׂł���B �E�ʐ^���ɂ���̂́ALTSpice�̐肤�������ł̕��`�g�����g�`�B �E�������ς�ƁALT�r���������̐肤�Ƃ���ł͈ʑ���ɂ͂R�X���e���K�v�Ƃ������ʂȂ̂����A���@�̕��`�g�����ł͂Q�O���e���œK�Ƃ̌��ʂł���A�����Ă��Q�O���e�ʼn����ł����R�Ȋ���������i�O�O�G�̂łQ�O���e�Ɍ��肵�����́B |
|
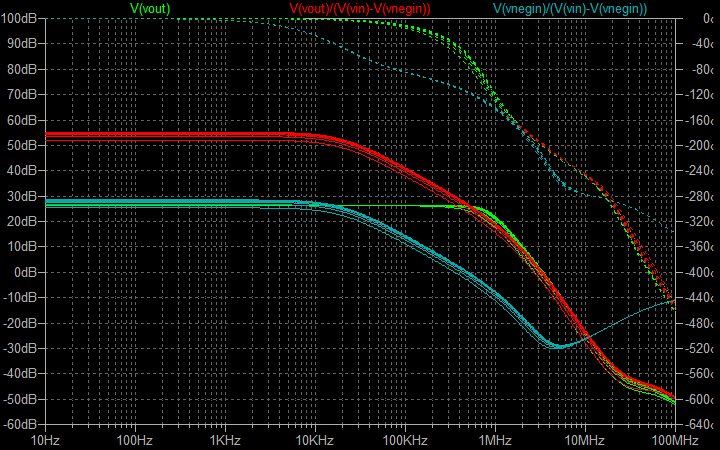
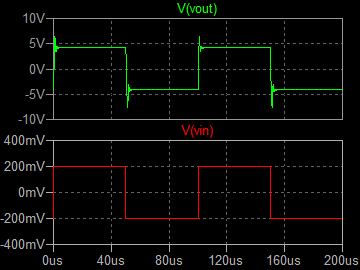
| �P�O���g���@�ʑ���P�O���e �Q�O���r�^div�@���O�D�QV�^div�@��TV�^div |
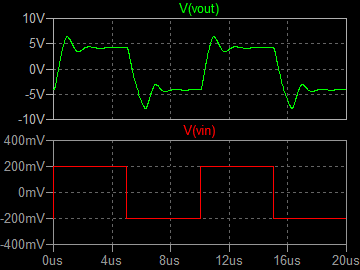
�P�O�O���g���@�ʑ���P�O���e �Q���r�^div�@���O�D�QV�^div�@��TV�^div |
 |
|
| �E�P�O���g�����`�g�����ʐ^�ł͌��ɂ������A�k�s�r���������̐肤�Ƃ�����`�g�̗����オ��A����������ɃI�[�o�[�V���[�g�Ƌ͂��ȃ����M���O���o�Ă���B����͂P�O�O���g�����`�g�����Ŗ��m�ɂȂ��Ă���B |
|
 |
 |
| �@�@�@�@ | |
| �P�O���g���@�ʑ���Q�O���e �Q�O���r�^div�@���O�D�QV�^div�@��TV�^div |
�P�O�O���g���@�ʑ���Q�O���e �Q���r�^div�@���O�D�QV�^div�@��TV�^div |
 |
|
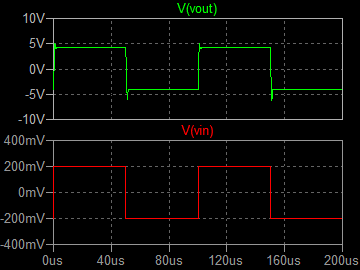
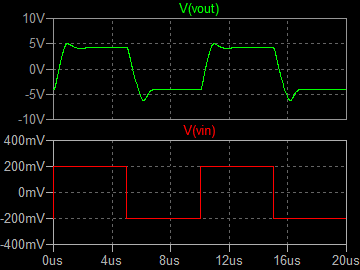
| �E�k�s�r���������̐肢�g�`�ł͂��̏ꍇ���܂��I�[�o�[�V���[�g���o�邪�A���@�̕��̕��`�g�����͍œK���B���f���p�����[�^�����d�������̂����炱�̕ӂ͂�ނȂ��B�i���j�i�O�O�G |
|
 |
 |
| �@�@�@�@ | |
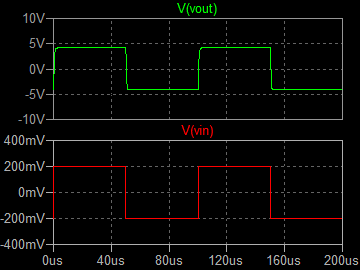
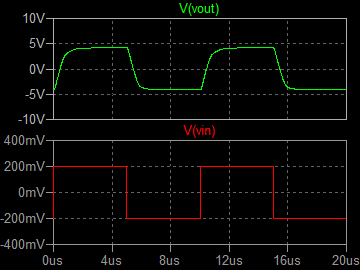
| �P�O���g���@�ʑ���R�X���e �Q�O���r�^div�@���O�D�QV�^div�@��TV�^div |
�P�O�O���g���@�ʑ���R�X���e �Q���r�^div�@���O�D�QV�^div�@��TV�^div |
 |
|
| �E�k�s�r���������̐肢�ł͂���ł悤�₭�I�[�o�[�V���[�g�����ł���B |
|
 |
 |
| �@�@ | |
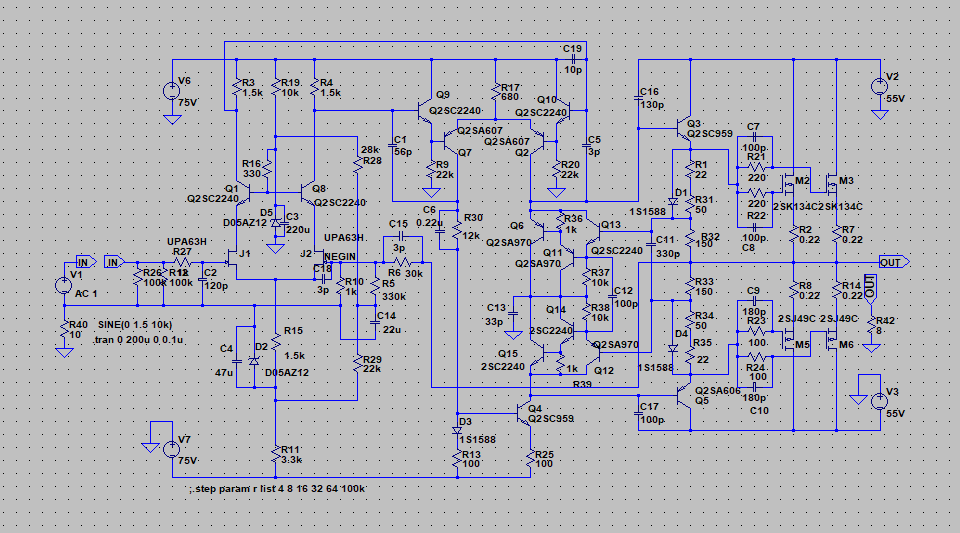
| �E�ƁA����ɂ͉�����肪�Ȃ��B �E�̂ŁA�������̏�ԂŃ��`�E���C�I���o�b�e���[��d���Ƃ��ĉ����Ă݂�B �E�s�`�c�QWAY�}���`�V�X�e���ŁA������h���C�u����䂪���c�d�r�����S�Ώ̌^���m���|�Q�O�X���ǂ����S�Ώ̌^�Ƃ��̂l�n�r�|�e�d�s �f�n�`�p���[�A���v�����ւ��ăq�������O����B �E���`��A�ǂ������킡�B�i�O�O�j �E���A���܂�ǂ��Ⴂ��������Ȃ��B�i���j �E�܂��A�ʎ��̂����Ȃ̂��낤����ǁB�B�B�i�O�O�G �E�����A�l�n�r�|�e�d�s�p���[�A���v�͂P�䂾���Ȃ̂ŁA�QWAY�}���`�ł͒�摤�����摤�ɂl�n�r�|�e�d�s�p���[�A���v���N�p���Ẵq�������O�ɂȂ���A���̂l�n�r�|�e�d�s�p���[�A���v���S���Ă����ш�����̃g�����W�X�^�p���[�A���v�ɖ߂��ƁA���O�Ɂg��������Ղ�H���F���H�������������B�h�Ƃ�����ۂ���̂ŁA�����̈Ⴂ�͂���悤���B����͂l�n�r�|�e�d�s�̕����F�Ō����R���g���X�g�����オ�����悤�Ȉ�ۂȂ̂�������Ȃ��B�t�Ɍ����ƁA�p���Ă���g�����W�X�^���Â����������邾�낤���A�䂪���c�d�r�����S�Ώ̌^�Ƃm���|�Q�O�X���ǂ����S�Ώ̌^�̉�����┖���H�����H�Ȃ̂����m��Ȃ��B�܂��A�ɒ��ɂ��āA�s�q�������̂l�n�r�������ɑ̂̐c��h���Ԃ�Ƃ����U��킷�悤�ȋɒቹ�܂ŏo���Ă���̂����A�s�`�c�@�s�k�|�P�U�O�P�`���h���C�u�������ł͂l�n�r�|�e�d�s�f�n�`�̕��������܂ʼn�����ۂ��Ă�������L�тĂ��銴��������B �E���A���̒��x�̈Ⴂ�Ȃ�A�킽�����I�ɂ͂ǂ���ł��ǂ��B |
|
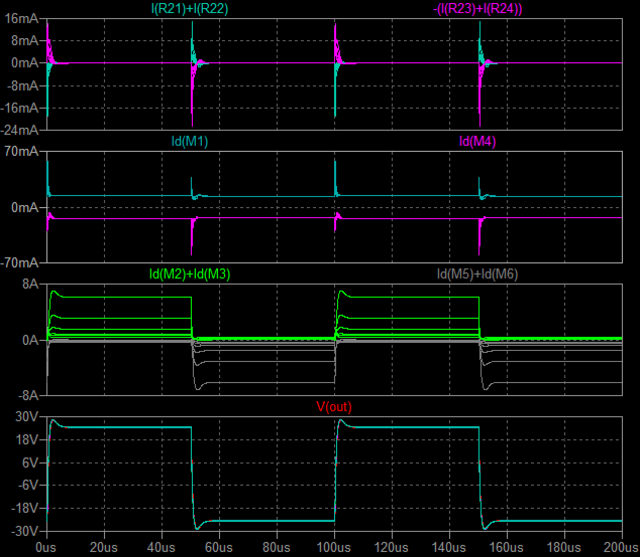
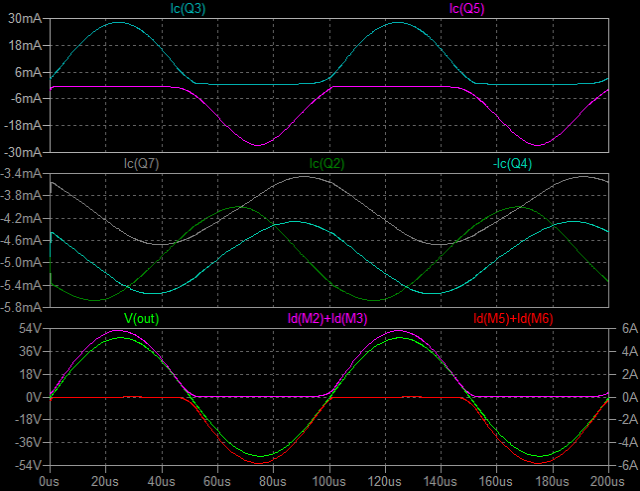
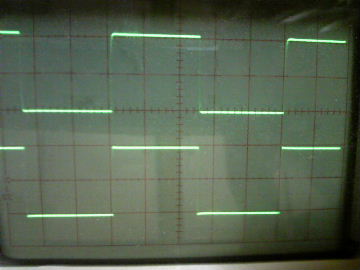
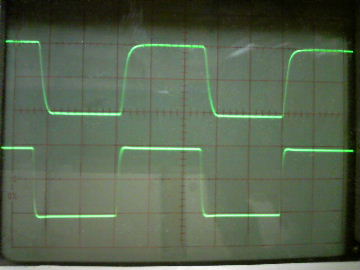
| �E�Ȃ̂ŁA���̂f�n�`�̂܂܂ōs�����ƂƂɂ����B �E�ƌ������ƂŁA�Ō�ɂقڍő�o�͂ɂ�������`�g�������ςĂ����B �E�P�O���g���ƂP�O�O���g���̕��`�g���������A���͂��P�u���|���Ȃ̂ŏo�͂͂Q�O�u���|�����Ă���A�d���d���I�ɂ���Ŗw�Ǎő�o�͂ł���B���E�ő�o�͓͂������`�E���C�I���o�b�e���}�P�T�u���g�p�����s�q�p���[�A���v�����ɔ�ׂ�Ƌ͂��ɏ��������قړ����x���B���������āA���̊��ł͑S���s���͂Ȃ��B |
|
| �P�O���g���@�����ׁ@ �Q�O���r�^div�@���O�D�TV�^div�@��P�OV�^div |
�P�O�O���g���@�����ׁ@ �Q���r�^div�@���O�D�TV�^div�@��P�OV�^div |
 |
 |
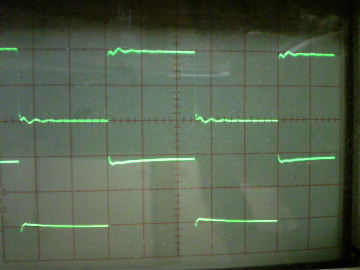
| �P�O���g���@���ׂP�O�� �Q�O���r�^div�@���O�D�TV�^div�@��P�OV�^div |
�P�O�O���g���@���ׂP�O�� �Q���r�^div�@���O�D�TV�^div�@��P�OV�^div |
 |
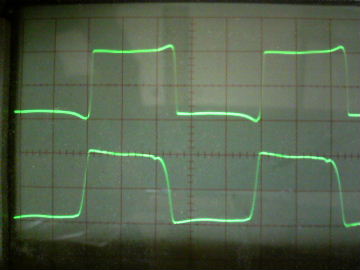 |
| �E�ϑ����̈����������Ă��P�O�����������o�͂Ƃ��g�`�������B�̂́A�䂪�s�q���s���S�Ώ̌^��m���|�Q�O�X���ǂ����S�Ώ̌^�ɓ��������A�����Ƃ̔�r�ł́A�P�O�O���g�����`�g�����͖������A�P�O�������Ƃ����̂l�n�r�|�e�d�s�p���[�A���v���ł��Y��ł���B |
|
| �@�@ | |
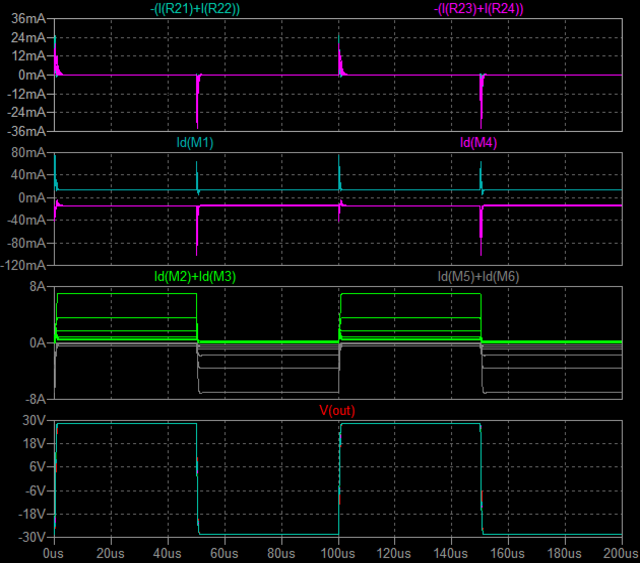
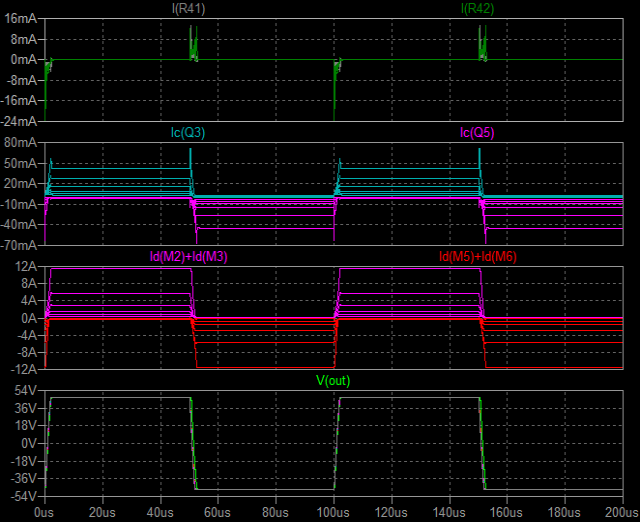
| �E�Ƃ������ʂ����č��ЂƂk�s�r���������œ������ɂ����閳�����̂P�O�O�j�g�����`�g�����Ă݂����Ȃ����B �E�ς����̂͏o�͉����g�`�ł͂Ȃ��A���̍ۂ̏I�i�l�n�r�e�d�s�ɗ����h���C���d���̕ω��ł���B �E���ꂪ�E���h���i�l�P�j�Ƃh���i�l�Q�j�ł��邪�A���������ƂɈُ�d�������ɏ��Ȃ��B�����ƌ����Ă��ǂ����炢���B��r�̂��߂ɂs�q�s���S�Ώ̌^�p���[�A���v�̏ꍇ�����ׂĂ��邪�A���҂̔�r���炻�̂��Ƃ����m���B �E�V�~�����[�V�����肢�̌��ʂ݂̂ł��̂������̂͌y���Ƃ������̂����A�������ꂪ�{���Ȃ�A�s�q�ɑ���l�n�r�̗D�ʐ��̈�����̕ӂɏo�Ă���̂����m��Ȃ��B |
|
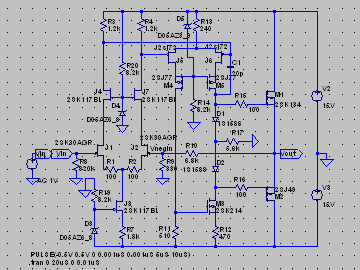 |
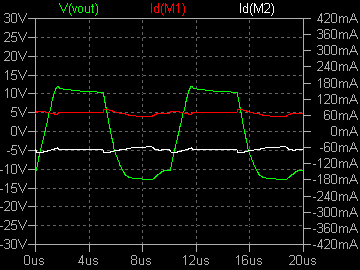 |
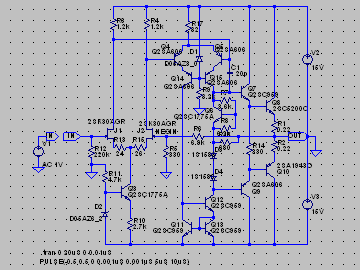 |
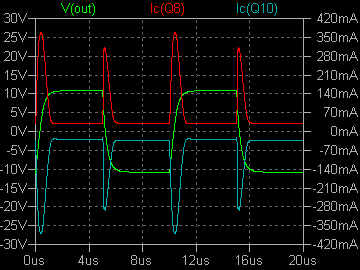 |
| �@�@�@ | |
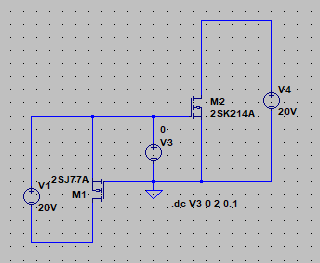
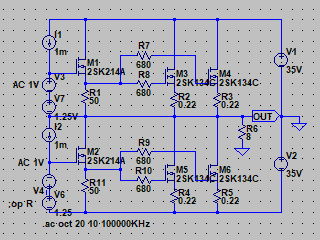
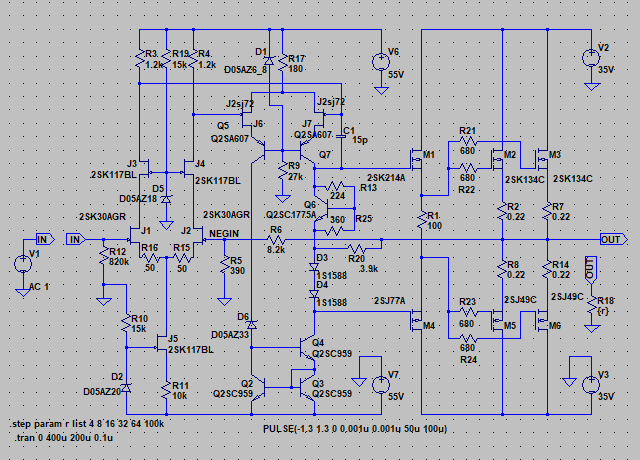
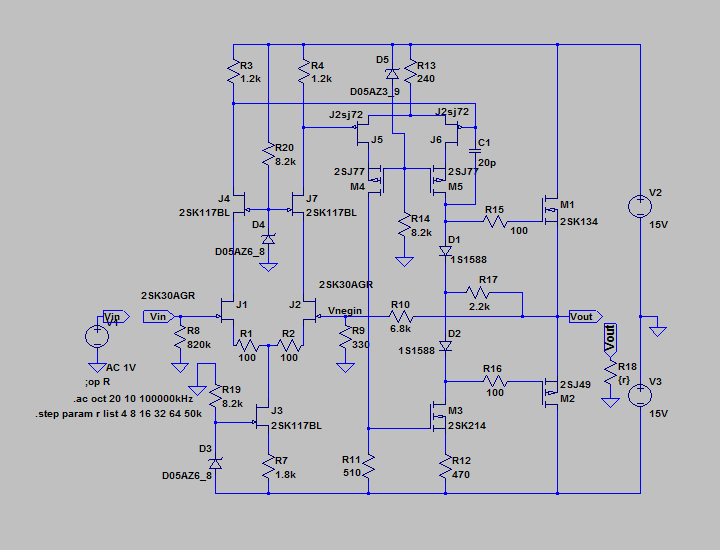
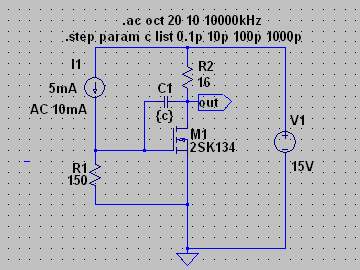
| �E�ƁA�����킯�ł��炭�l�n�r�|�e�d�s�f�n�`�p���[�A���v�Ƃ��Ē����Ă����B �E�̂����A�����u�s���S�Ώ̌^�v�ɂ�����ǂ����낤���A�Ǝv���Ă��܂��B�i�O�O�G �E�̂ŁA����Ă݂�B �E��������ɂ́A���̂悤�ɂf�n�`��R�̂Ȃ�����A�[�X���犮�S�Ώ̌^���l�ɏo�͓_�ɕς��邾���B �E��������Ƃǂ��Ȃ邩�͂s�q���̕s���S�Ώ̌^�p���[�A���v�ŕ������Ă��邪�A�ꉞ�A���ׂ̂q�P�W���S���A�W���A�P�U���A�R�Q���A�U�S���A�T�O�����i���׃I�[�v�������j�̏ꍇ�̃p�����g���b�N��͂ŁA���̏�Ԃɂ����闘�����ʑ��|���g���������k�s�r���������ŊςĂ����B |
|
 |
|
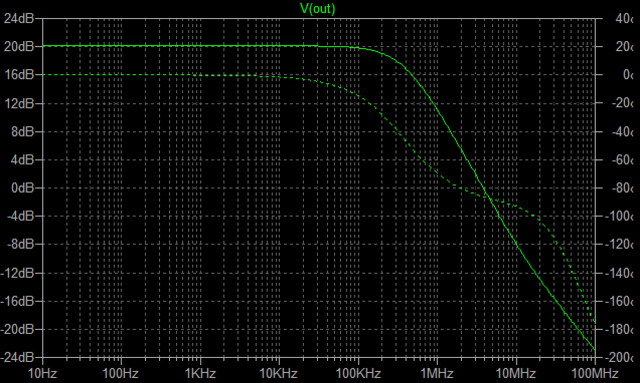
| �E���̓����́A���S�Ώ̌^���l�ɃI�[�v���Q�C���i�ԁj�����ׂɔ�Ⴕ�đ�����������ɂȂ�B �E�N���[�Y�h�Q�C���i�j�͓��R���Ȃ̂ŁA���ʃ��[�v�Q�C���i�j�i���m�e�a�ʁj�����ׂɔ�Ⴕ�đ�������B�v����ɂj���Ō����Ƃ���̑��x�^���[�V���i���t�B�[�h�o�b�N�i�l�e�a�j���|���鏊�Ȃ̓����ł���B �E���̏ꍇ�I�[�v���Q�C���͂q�P�V�Œ����\�ł��邪�A������Q�D�Q�����ɂ����̂́A�I�[�v���Q�C�����ŋߍ�������̂s�q���s���S�Ώ̌^�p���[�A���v�⌳�c�d�r�����S�Ώ̌^�p���[�A���v�ɍ��킹�邽�߁B �E���ʁA���ׂW���̏ꍇ�̃I�[�v���Q�C���͒��łU�O���a���x�ƁA�f�n�`�`���̏ꍇ���V���a���x�傫���Ȃ�B �E���̕ύX�������Ă��A������������ʑ��|���g�������͏��i�e�d�s�̂����ƂQ�i�ڍ����A���v�f�|�c�Ԃ̈ʑ���R���f���T�[�̂Q�҂݂̂ɂ���ċK�肳��邽�߁A���̏ꍇ�ł��R�O���g�����x�ȏ�̗̈�̓����ɂ͉��̕ω��������Ȃ��B�̂ŁA�ʑ����������K�v�͂Ȃ��B |
|
 |
|
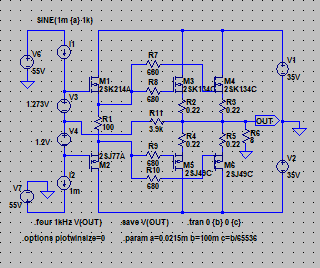
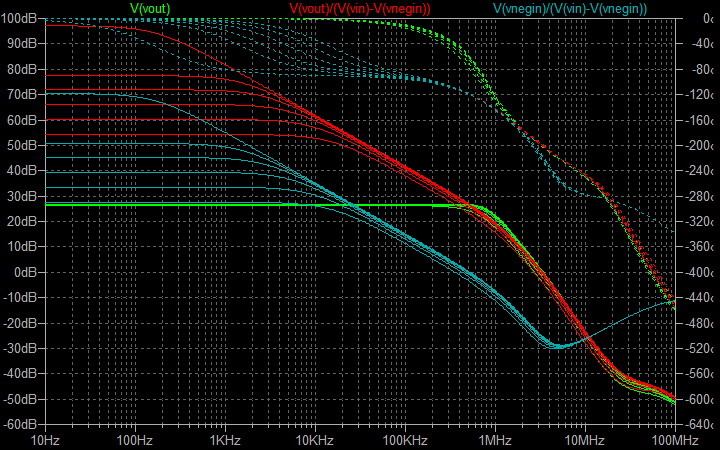
| �E�Ƃ����u�s���S�Ώ̌^�v�Ȃ̂����A���̎��Ԃ͂�����w�Ȃ��̂ł͂Ȃ��B �E�A�[�X�Ɍq�����Ă����f�n�`��R���u�[�g�X�g���b�v��R�ɂȂ��������ł���B �E�u�[�g�X�g���b�v�ƌ����A�j���m���|�P���o�ꂷ�鍠�̂P�X�V�O�N�㏉���̍��Y�p���[�A���v�ɗǂ��g���Ă����炵���B����́A�A���v�o�͓_����Q�i�ړd�������i�̒�R���ׂ̒��_�ɑ�e�ʂ̃u�[�g�X�g���b�v�R���f���T���Ȃ����̂����A���̒�R������Ɩ{���I�ɓ������̂ł���B �E�������A���̏ꍇ�I�i�͂l�n�r�œ��̓C���s�[�_���X�͂������������������A�Q�i�ڂ���R���ׂł͂Ȃ��o�̓C���s�[�_���X�̍����J�����g�~���[���ׂȂ̂ŁA�P�X�V�O�N�����̍��Y�p���[�A���v�Ŏg�p����Ă����炵���u�[�g�X�g���b�v�Ɠ��l�̂��̂����̉�H�ŗp����Ӌ`�͑S���Ȃ��B�̂����A���̂悤�ɂj���Ō����Ƃ���̑��x�^���[�V���i���t�B�[�h�o�b�N���|����I�[�v���Q�C��������������Ƃ����_�ŋN�p����B �E���̈Ӗ��ł͓������̂ł��ړI�A�p�@���Ⴄ�Ƃ������Ƃł���B �E���Ȃ݂Ɋ��S�Ώ̌^�̏I�i�㑤�̓��������Ɠ��l�̃u�[�g�X�g���b�v�^�Ȃ̂ŁA����炪�����悤�ȓ����������͓̂��R�ł���B�v����A�����̃u�[�g�X�g���b�v��H��d���h���C�u����̂��u���S�Ώ̌^�v�ł���A�u�s���S�Ώ̌^�v�ł���B�Ƃ������ƂɂȂ�B �E�ƁA�����Ƃ�����k�s�r���������Ő���Ă݂�B |
|
| A�@�^ | |
  |
|
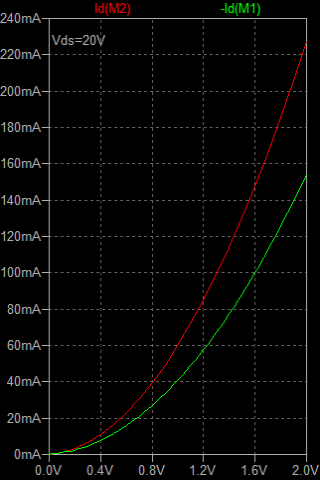
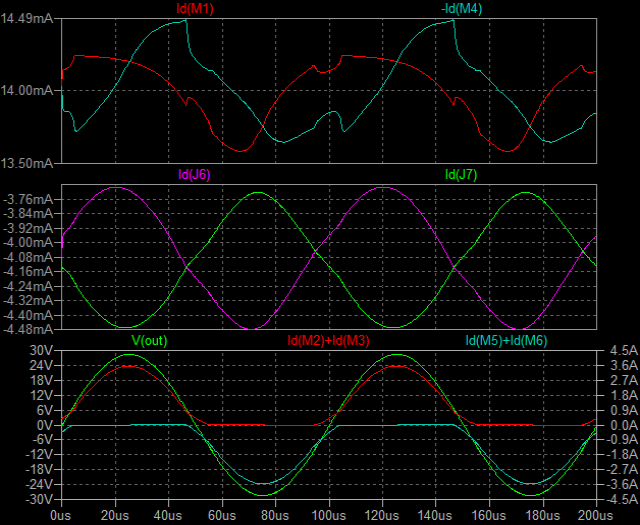
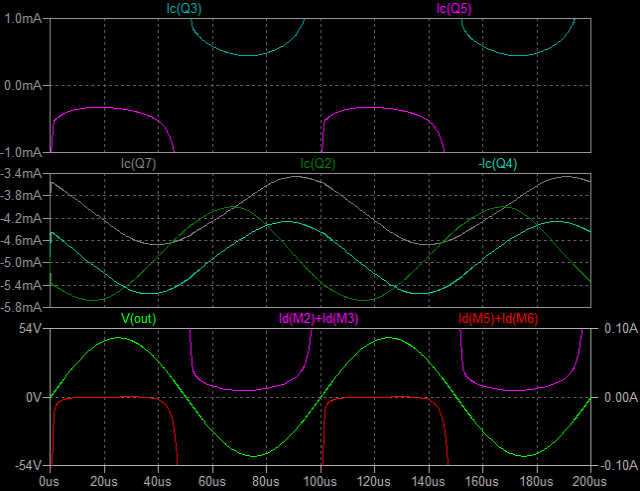
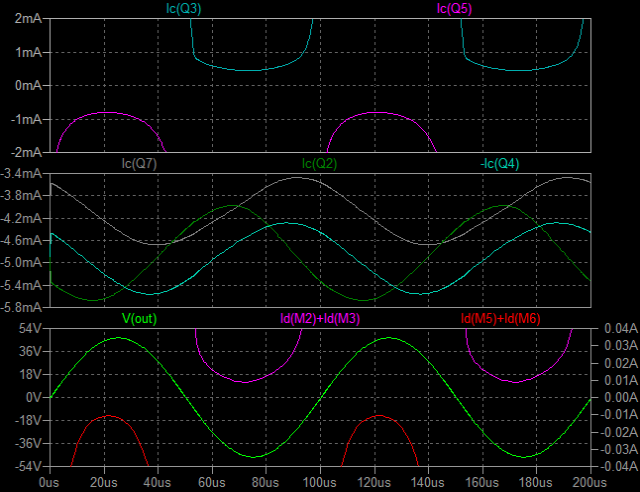
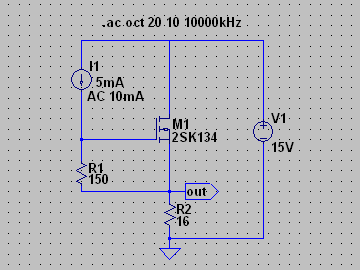
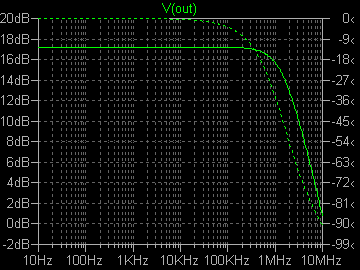
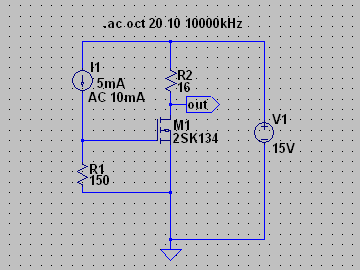
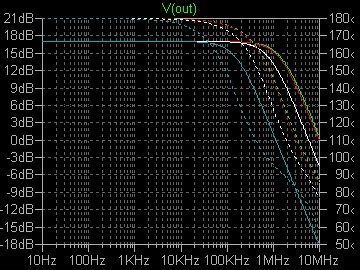
| �E���̂`�^�́A���S�Ώ̌^�I�i�̏㑤�ł���B�O�i����T���`�̓���_�d���������ƂƂ��ɁA�����g�M�����P�O���`���|���ʼn�������Ƃ����ݒ�B �E���̌��ʂ͉E�̒ʂ�A�������P�V���a�A�������P�D�R�l�g���Ƃ����������ɂȂ��Ă���B |
|
| B�@�^ | |
 |
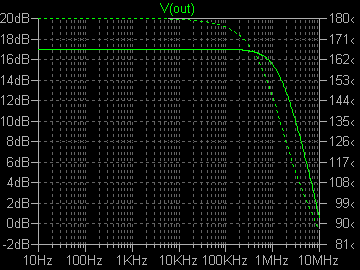 |
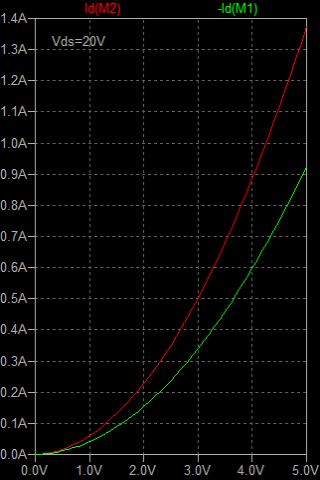
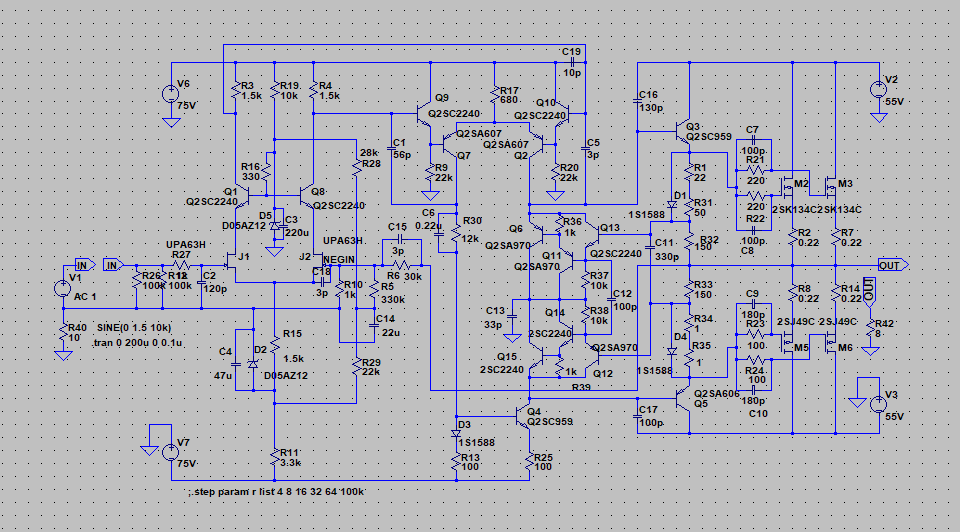
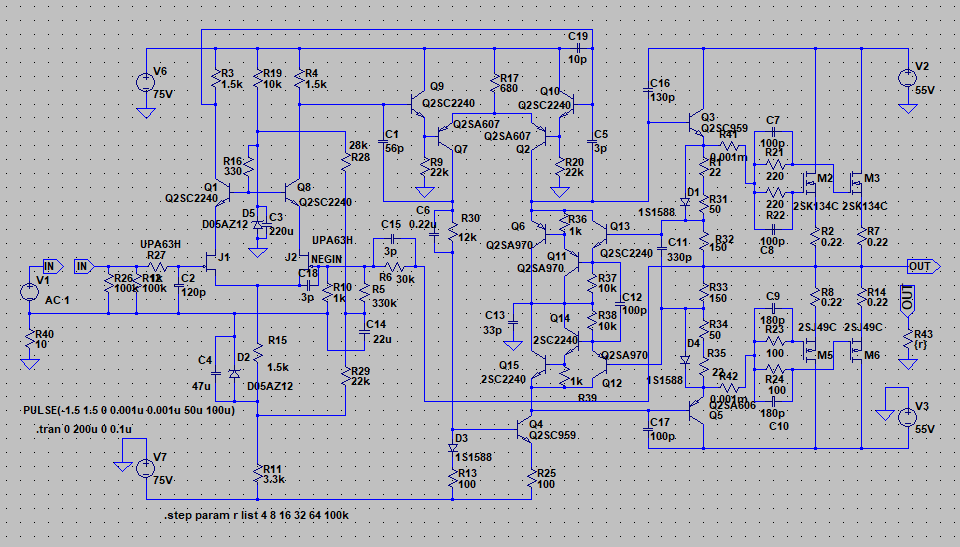
| �E���ɂa�^�B������͊��S�Ώ̌^�I�i�̉����ł���B�ݒ�͂`�^�ƑS�������ŁA�����Q�r�j�P�R�S�̕��ׂƂȂ�q�Q�̈ʒu���\�[�X������h���C�����Ɉڂ��Ă���B �E�ŁA���̗����Ƃ��̎��g���͉E�̒ʂ�ł��邪�A������������P�V���a�A�������P�D�R�l�g���ƁA�`�^�Ɠ����ł���B �E�̂́A�`�^�Ƃa�^�ł̓C���s�[�_���X���O���ł���d���u�P�̈ʒu�����ג�R�q�Q�̏ォ�����̈Ⴂ�ŁA���̂u�P��Z�����Č���Ζ��炩�Ȃ悤�ɁA���������S���������̂ł��邩���A������O�ł����B �E���A���̂a�^�͂`�^�ƈ���ău�[�g�X�g���b�v�ł͂Ȃ��B���ȏ��I�ɂ����Ƃ���̃\�[�X�ڒn�^�i�\�[�X���ʌ^�j���B�ƌ����킯�ŁA���ǃ\�[�X�ڒn�^�Ɠd���h���C�u�̃u�[�g�X�g���b�v�^�͓������̂ł���B |
|
| �E�z���g�����ȁH���Ȃ��Ƃ��Q�[�g�|�h���C���Ԃ̊e�ʂɂ��~���[���ʂ͈Ⴄ�̂ł́H �E�Ȃ̂ŁA�f�|�c�Ԃɂ킴�ƂO�D�P���e�i�Ȃ��ɑ����j�A�P�O���e�A�P�O�O���e�A�P�O�O�O���e���Ȃ��p�����g���b�N��͂Ŋς�B |
|
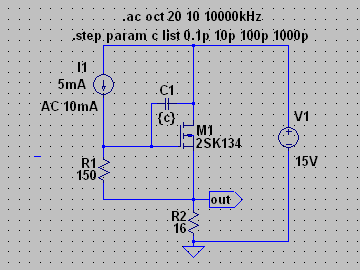 |
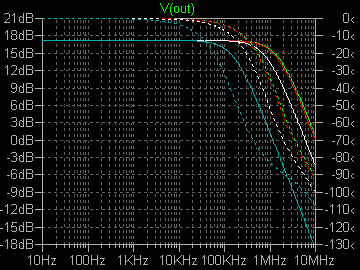 |
| �E���ʂ͈ʑ������]���Ă��邾���ŁA�S�������B�\�[�X�ڒn�^�Ɠd���h���C�u�̃u�[�g�X�g���b�v�^�͓������̂Ȃ̂œ�����O�B |
|
 |
 |
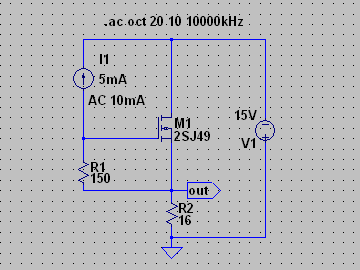
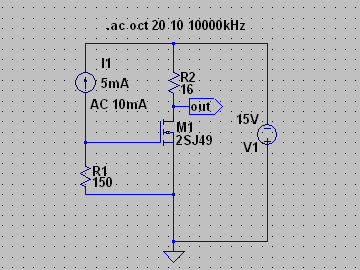
| �E�o�`�����l���̂Q�r�i�S�X�œ��l�Ɋς��̂��b�^�Ƃc�^�B | |
| C�^ | |
 |
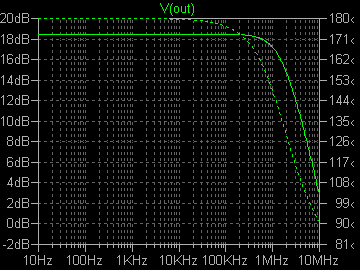 |
| D�^ | |
 |
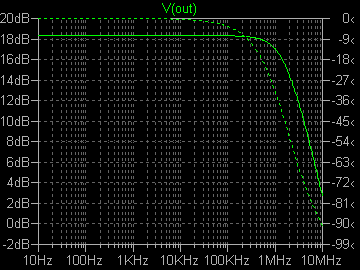 |
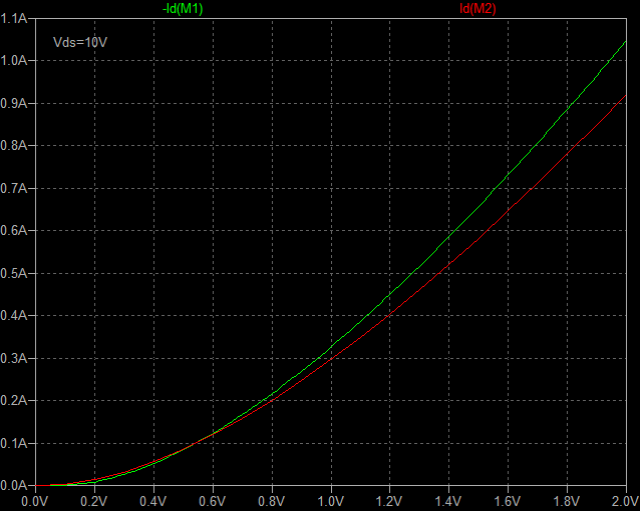
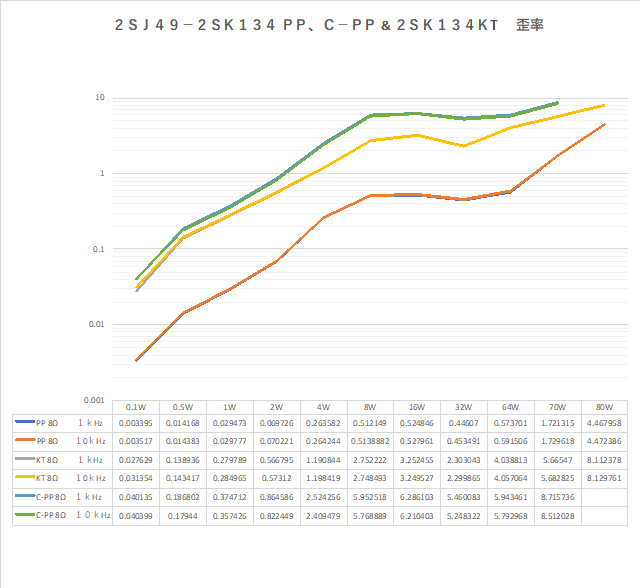
| �E���R�����A�ǂ�����������P�W�D�Q���a�A�������P�D�T�l�g���ƁA��������Q�r�j�P�R�S�̏ꍇ�Ɠ������ʁB �E���A�Q�r�j�P�R�S�̂`�^�A�a�^�ƂQ�r�i�S�X�̂b�^�A�c�^�̌��ʂ��ׂ�Η����������������قȂ�B�̂́A�R���v���f�q�Ƃ͌����A�ʂ̑f�q�ł��邩�瓖�R�ł���B �E���̏ꍇ�ɂQ�r�i�S�X�̕����������傫���̂́A�O�i����T���`�̓���_�d���łq�P���P�T�O���ɔ�������o�C�A�X�d���ŗ����A�C�h�����O�d�����A���̂r�����������f���ł͂Q�r�j�P�R�S���U�V���`�Ȃ̂ɑ��A�Q�r�i�S�X�̕��͂P�P�R���`�Ƒ����A���̕��Q�r�i�S�X�̂������傫���Ȃ邽�߂ł���B �E�����ɂ��̓���_�d�������ĂQ�r�i�S�X�̃A�C�h�����O�d�����U�V���`�ɂȂ�悤�ɒ�������ƁA���̏ꍇ�̗����͂P�U�D�Q���a���x�ƂȂ����B����_�𑵂��Ă��Q�r�j�P�R�S�Ƃ͈�v���Ȃ��B ���Ƃ��ƈႤ�f�q�Ȃ̂�����A�����������O�B |
|
| �E�ȏォ��A�Q�r�j�P�R�S�̂`�^�Ƃa�^�A���邢�́A�Q�r�i�S�X�̂b�^�Ƃc�^��g�ݍ��킹�ăv�b�V���E�v�������������Ƒ�ϗǂ����z�I�Ȍ��ʂ������邱�Ƃ��\�z����邪�A���������̂��u���S�Ώ̌^�v�Ƃ������ƂɂȂ�B �E����f�q�ꓮ��őg�ݍ��킹��̂�����v�b�V���v���Ƃ��Ă���ȏ�Ώ̂ȓ���͂Ȃ��B�]���Ă��̑g�ݍ��킹���u���S�Ώ̌^�v�Ɩ����͓̂K�ł���B |
|
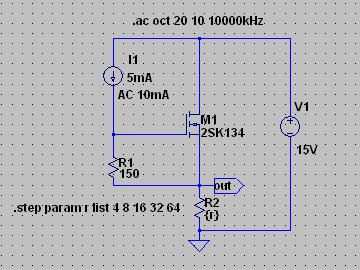
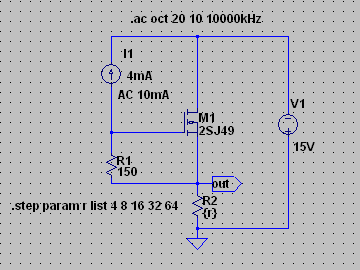
| �E���A����A�Q�r�j�P�R�S�̂`�^�A�a�^�̌��ʂƂQ�r�i�S�X�̂b�^�A�c�^�̌��ʂ͂���ȂɈ��Ȃ��ł͂Ȃ����B�Ƃ��v����B�i�O�O�G �E�̂ŁA���̍ۂQ�r�j�P�R�S�̂`�^�ƂQ�r�i�S�X�̂b�^��g�ݍ��킹���v�b�V���E�v������������悤�Ƃ����̂��u�s���S�Ώ̌^�v�B �E�����ŁA�Q�r�j�P�R�S�ƂQ�r�i�S�X�̃A�C�h�����O�d���𑵂��āA���ꂼ��̕��ג�R���S���A�W���A�P�U���A�R�Q���A�U�S���ƕω��������ꍇ�̗��������̈ʑ��̎��g���������p�����g���b�N�ɐ���Ă݂�ƁA�����Ȃ�B |
|
 |
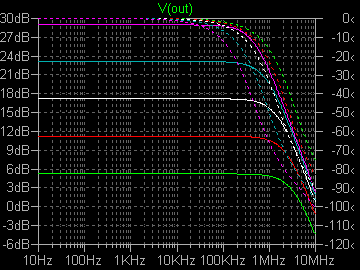 |
| �E�ǂ���������畉�ׁ��q�Q���S���A�W���A�P�U���A�R�Q���A�U�S���̏ꍇ�����A�����͂ǂ�������ׂ̂U���a�X�e�b�v�̑����ɔ�Ⴕ�ĂU���a�X�e�b�v�ő�������B����́u���S�Ώ̌^�v�Ɠ����Ƃ��낾�B �E���A���ҊԂł͗����ɂP���a���x�̘���������B����͑f�q���Ⴄ�̂����炢����Ƃ����������Ƃ���B |
|
 |
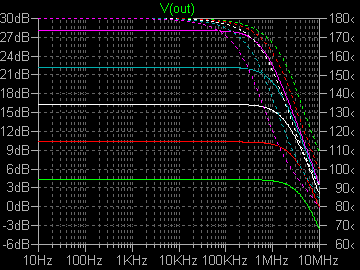 |
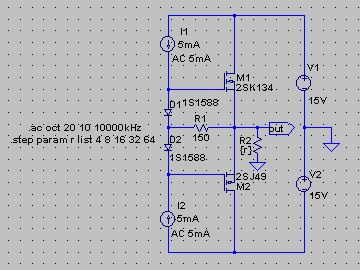
| �E���A���̒��x�̈Ⴂ������ʂĂ����傤���Ȃ��̂ł́H�Ƃ��������I�ȍl���ŁA�Q�r�j�P�R�S�̂`�^�ƂQ�r�i�S�X�̂b�^��g�ݍ��킹���v�b�V���E�v�������������Ƃ����Ȃ�B�Ȃ��A�M���d�����T���`���|���Ƃ��Ă���̂́A���̏ꍇ�v���X�}�C�i�X����v�b�V���v���ŏI�i���h���C�u���邩��ł���B���ʁA��̃V���O������̏ꍇ�ɔ䂵�Ă�����̕��ׂ̏ꍇ���������U���a�������Ă���B�����ʂ肾�B |
|
 |
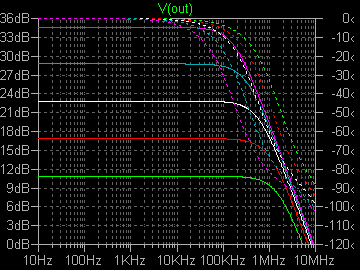 |
| �E�ƁA����̑Ώ̐��Ƃ����Ӗ��ł͖ܘ_���S�ł͂Ȃ��̂Łu���S�Ώ̌^�v�͖����Ȃ����A������e�́u���S�Ώ̌^�v�Ɠ����ł��邵�A����ł������͂Ȃ��̂ł́A�Ƃ����̂��u�s���S�Ώ̌^�v�B �E�Ȃ̂����A���́u�s���S�Ώ̌^�v�ɂ������b�g������B �E����́A�I�i�̃o�C�A�X��H���u�[�g�X�g���b�v��R���番���ł��A�I�i�㉺���v�b�V���v���Ńh���C�u�ł��A���ɏI�i���g�����W�X�^�ō\�������ꍇ�ɂ͕����ł����o�C�A�X��H�ŏI�i�̉��x�⏞���ȕւ������Ɏ��{�ł���_�ł���B���̓_�́u���S�Ώ̌^�v��薾�炩�ɗL���ł���B |
|
| �E���A������������傤���Ȃ��B�̂ŁA���������Ă݂�B �E���`��A�ǂ������킡�B�i�O�O�j �E�������QWAY�}���`�ŁA��摤�����摤�ɂl�n�r�|�e�d�s�p���[�A���v���N�p���Ẵq�������O�ɂȂ���A��͂�l�n�r�|�e�d�s�p���[�A���v�̕����S��ŐF�ɗႦ����̃R���g���X�g�������F�ʊ����L���ŁA���ł͂P�I�N�^�[�u���܂ʼn��悪�L�������悤�ɃG�l���M�[���̋����ɒቹ���o���Ă���B���ǂf�n�`�̂Ƃ��ƈ�ۓI�ɂ͓����Ȃ̂����A���̌X������薾�m�ɂȂ����悤�Ɋ�����B�ŁA�[�I�Ɍ����A��r�I�ɂs�q���W�łl�n�r���Z�B�ǂ��炪�ǂ����H�ƂȂ�Ƃǂ�������̂l�n�r�|�e�d�s�s���S�Ώ̌^�p���[�A���v�̏������Ȃ��B�B�B �E���A�ʎ��̂���������A�l�n�r�|�e�d�s�s���S�Ώ̌^�łȂ���Β����Ȃ��Ȃ����A�ƌ����悤�Ȃ��Ƃ͂Ȃ��B�s�q���S�Ώ̌^�̕����\���ɗǂ������B �E�ŁA���_�Ƃ��Ă͂f�n�`�^�ł͂Ȃ��s���S�Ώ̌^�ōs���B |
 |
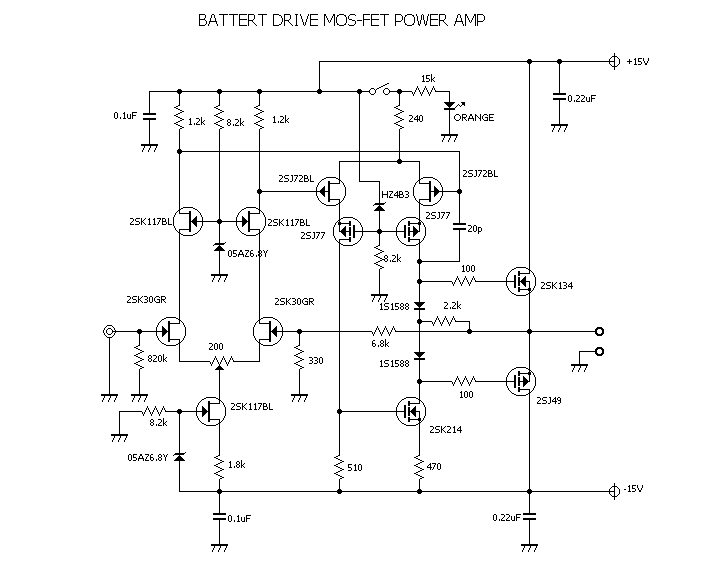
| �E�ƌ����킯�ʼn�H�͂����B �E���̍ۃp�C���b�g�����v�̂k�d�c�̓A���[�g�F�̐Ԃ͎~�߂Ğ�F�ɂ����B |
|
 |
|
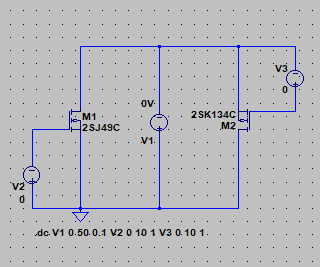
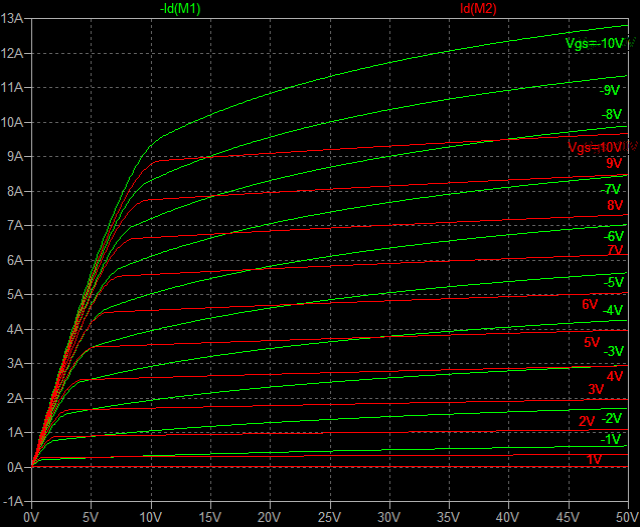
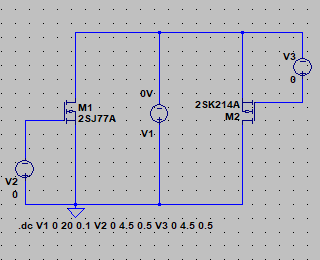
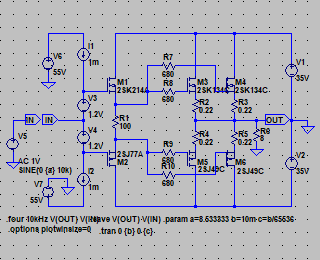
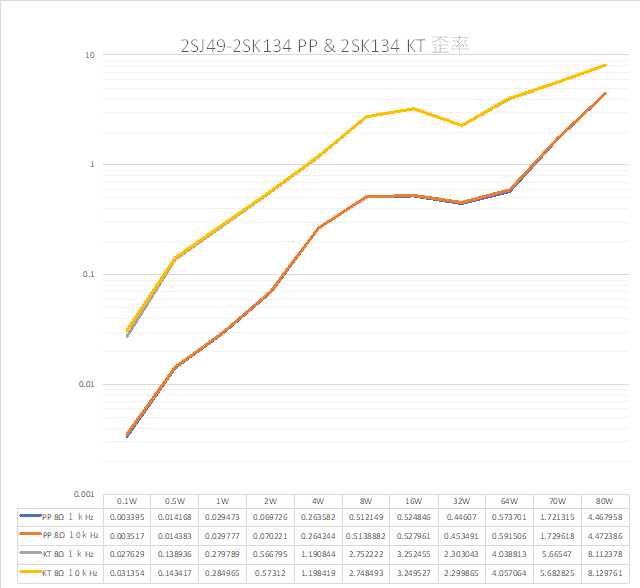
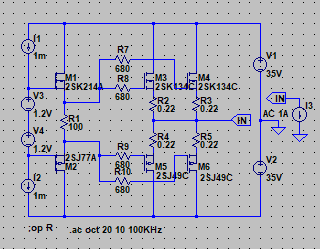
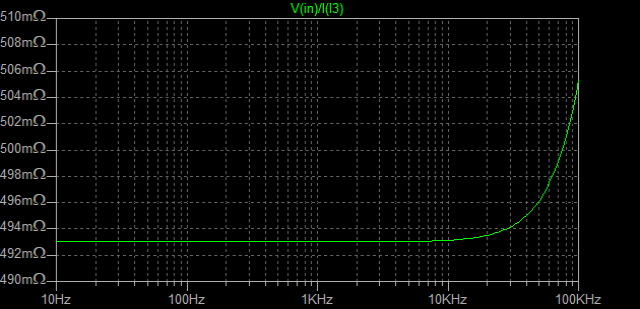
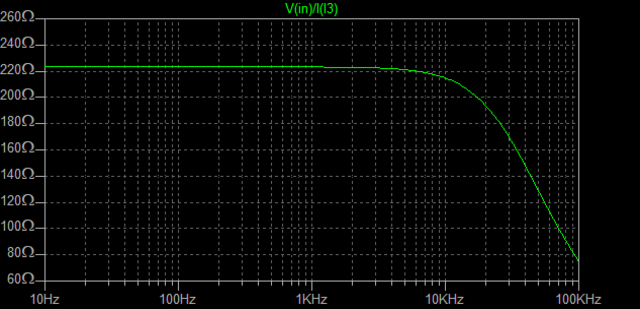
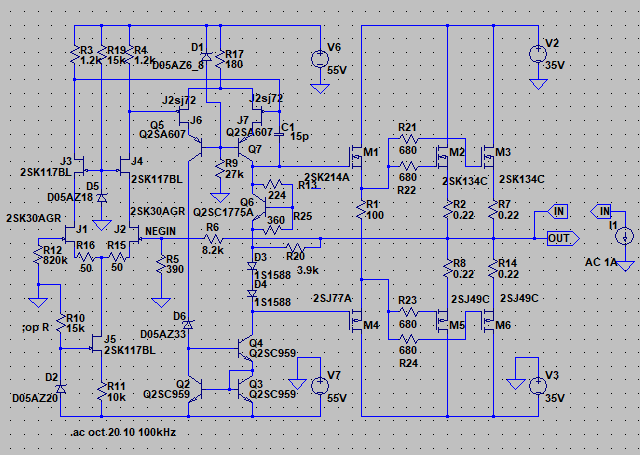
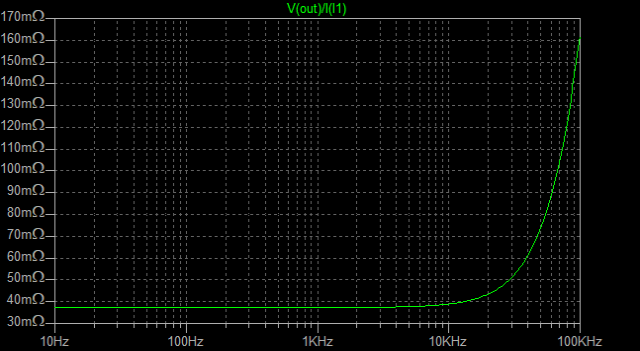
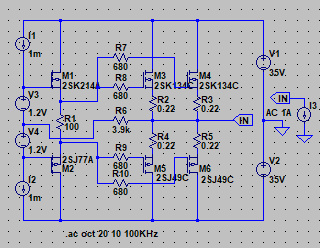
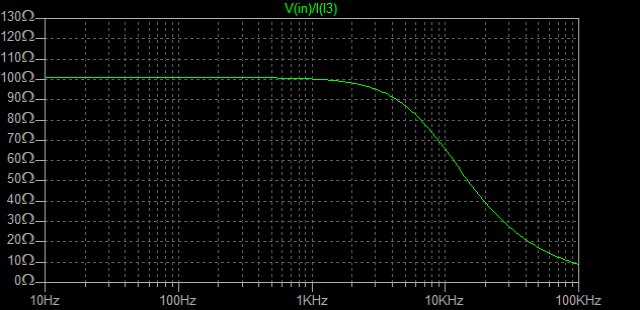
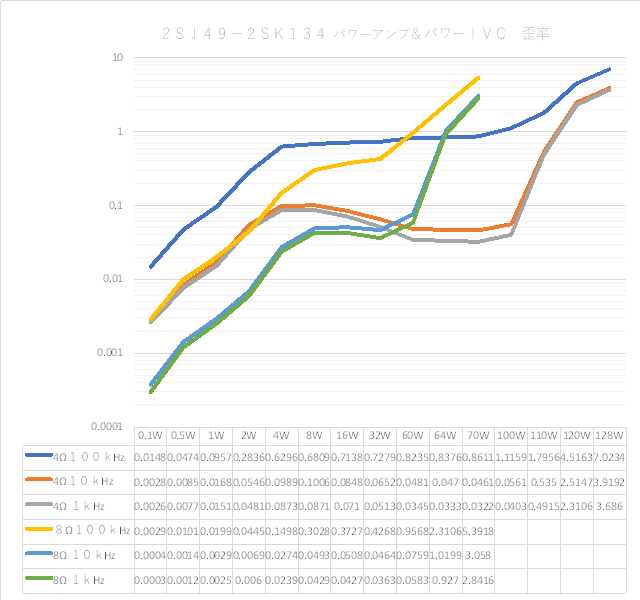
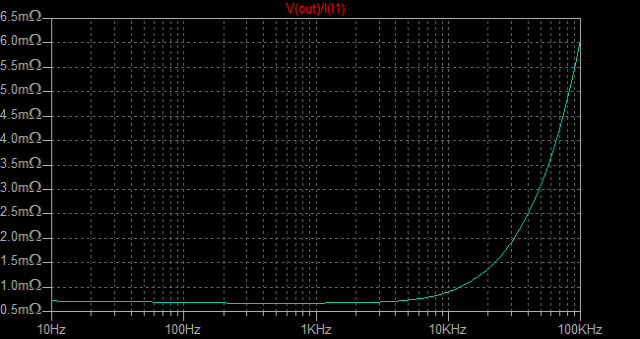
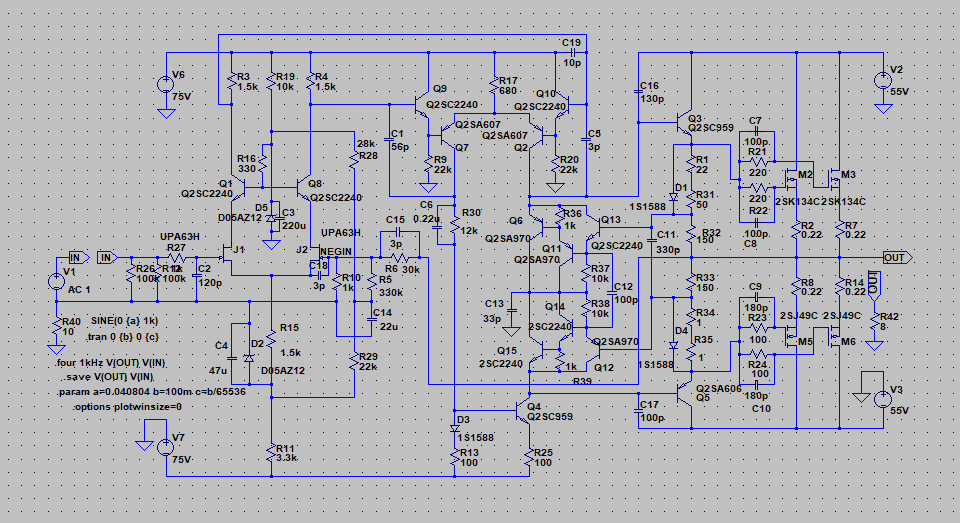
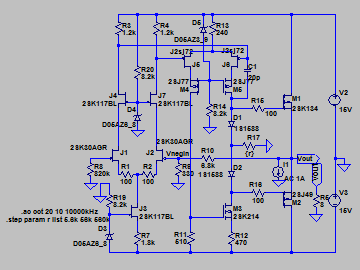
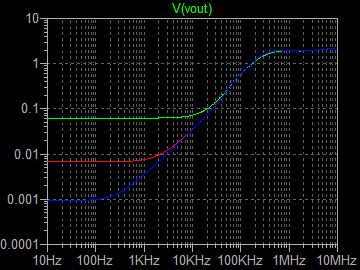
| �E�Ƃ���ŁA�f�n�`�^�ƕs���S�Ώ̌^�̑����̉��̈Ⴂ�̗v�����j���̂�����l�e�a�ȊO�ɂ�����̂��ۂ������l���邽�߂ɁA���^�C�v�̏ꍇ�̏o�̓C���s�[�_���X�𑪒肵�Ă݂�B �E���@�́A���ׂq�P�Ƃq�Q��p�ӂ��āA�q�P�����̏o�͓d���Ƃq�Q�����̏o�͓d�����狁�߂���@���̗p�����B �E�q�P�����̏o�͓d�����u���P�A�q�Q�����̏o�͓d�����u���Q�A�o�̓C���s�[�_���X���y���Ƃ���A�A���v�{���̋N�d�́i�u�Ƃ���j���y���Ƃq�P���͂q�Q�ŕ�������Ău���P���͂u���Q�̏o�͓d���ƂȂ锤�Ȃ̂ŁA �@�u���P���q�P�^�i�y���{�q�P�j���u �@�u���Q���q�Q�^�i�y���{�q�Q�j���u�@ �@������ �@�i�q�P�{�y���j���u���P�^�q�P���i�q�Q�{�y���j���u���Q�^�q�Q �@������y���ɂ��ĉ����ƁA �@�y�����q�P���q�Q���i�u���Q�|�u���P�j�^�i�q�Q���u���P�|�q�P���u���Q�j �@�ŏo�̓C���s�[�_���X�����߂���B �@������A�q�Q���Q�q�P�����Ă��鎞�i�W���ƂP�U���Ƃ��S���ɂW���Ƃ��j�ɂ� �@�y�����Q���q�P���i�u���Q�|�u���P�j�^�i�Q���u���P�|�u���Q�j �E���ʁA���̂l�n�r�|�e�d�s�p���[�A���v�́A�f�n�`�`���ł͂S�O�O�g�������g���͂łW�������ɂS�D�O�U�S�u�̏o�͂ƂȂ�ݒ�łS���ׂɂ���ƂR�D�X�V�U�u�̏o�͂ƂȂ����B�̂ŁA���̏o�̓C���s�[�_���X�͂O�D�P�W�P���B �E�s���S�Ώ̌`���ł́A�������S�O�O�g�������g���͂łW�������ɂS�D�O�V�U�u�̏o�͂ƂȂ�ݒ�łS���ׂɂ���ƂR�D�X�R�U�u�̏o�͂ƂȂ����B�̂ŁA���̏o�̓C���s�[�_���X�͂O�D�Q�X�T���B �E�ĊO���ҊԂɂ��܂�Ⴂ�̂Ȃ����ʂ��B �E���̕ӂk�s�r���������̐肢�ł͂ǂ����B �E�V�~�����[�V�����ł͉���Ƃ����S�z������Ȃ��̂ŏo�͂ւ̓d�������@�ł���Ă݂�B�����������d���͂P�`�B��������ƌ��ʂ����ŕ\�����ꂩ�瑢�삪�Ȃ��ĕ֗��B �E�悸�͂f�n�`�^�B�f�n�`��R���T�D�U�����A�T�U�����A�T�U�O�����Ƃ���p�����g���b�N��́B �E���ʂ͉E�ŁA���T�D�U�����̏ꍇ�A�Ԃ��T�U�����̏ꍇ�A���T�U�O�����̏ꍇ�B��͂�o�̓C���s�[�_���X�͂f�n�`��R�̐ݒ�ɂ��I�[�v���Q�C���̑������m�e�a�ʂ̑����ɔ�Ⴗ��悤���B�ŁA���@�Ɠ����f�n�`��R���T�D�U�����̏ꍇ�̏o�̓C���s�[�_���X�͒��łO�D�O�U�����x�Ƃ����肢���ʂł���B |
|
 |
 |
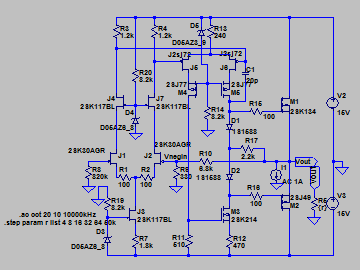
| �E���ɕs���S�Ώ̌^�B�u�[�g�X�g���b�v��R�͎��@�ɓ������Q�D�Q�����B���x�͕��ׂ��S���A�W���A�P�U���A�R�Q���A�U�S���A�T�O�����i�����ב����j�Ƃ���p�����g���b�N��́B �E���ʂ͕��ׂƂ͖��W�ɒ��łO�D�P�U�����x�Ƃ����肢���ʁB �E���`�ށB�B�B�s���S�Ώ̌^�͕��ׂɂ���ăI�[�v���Q�C�����ς��A���������Ăm�e�a�ʂ��قȂ�̂ŁA���ׂɂ���ďo�̓C���s�[�_���X���قȂ���̂Ǝv���Ă����̂����A���ׂ̒l�ɂ͖��W�̂悤���B������ƕs�v�c�B�i�O�O�G |
|
 |
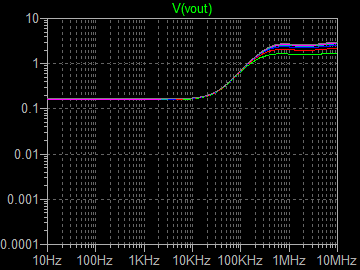 |
| �E�ƌ����킯�Ŏ����̕������������o�Ă��邪�A�V�~�����[�V�����ł����@�Ɠ��l�ɕs���S�Ώ̌^�̏o�̓C���s�[�_���X���f�n�`�^���O�D�P�����x�����Ƃ������ʂł��邩��A�����l�͂��܂�ԈႢ�̂Ȃ����ʂƍl���ėǂ����낤�B �E�ƂȂ�ƁA�O�D�P�����x�̏o�̓C���s�[�_���X�̈Ⴂ�ł́A���ꂪ�f�n�`�^�ƕs���S�Ώ̌^�̉��̍��̗v���ɂȂ��Ă���Ƃ͍l���ɂ����B�Ƃ������ʂ��B |
|
| �E����͒u���Ă����Ƃ��āA���E�ŏ��̂l�n�r�|FET�B �E�g�����̃p���[�f�q�h�������̂����A�Ȃ�ł���Ȃɗǂ����Ȃ̂��B�B�B�i���j |
|
 |
|