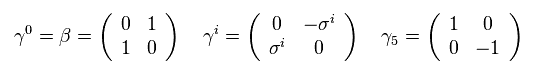
Top page (correct Bohr model including helium. )
Supersymmetry is a waste of money.
(Eq.1)
On this page, we use the notations of this site.
Eq.1 is the chiral expression of γ matrices.
Only on this page, ( 1, -1, -1, -1 ) version of metric tensor is used.
And σ is Pauli matrices, which are
(Eq.2)
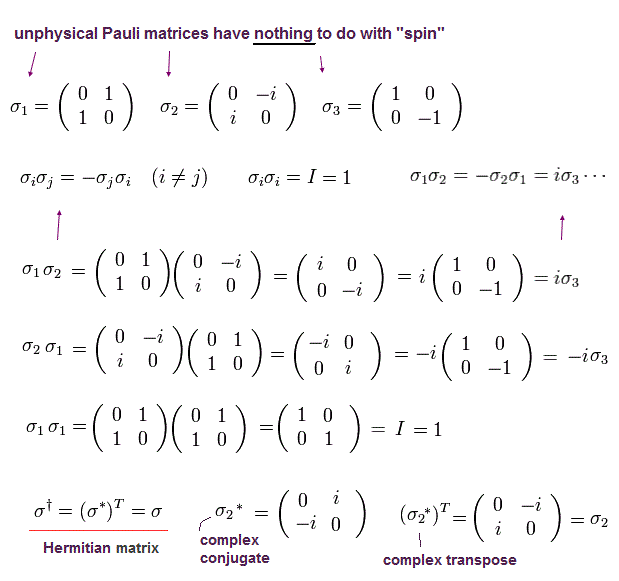
From Eq.1, we have
(Eq.3)
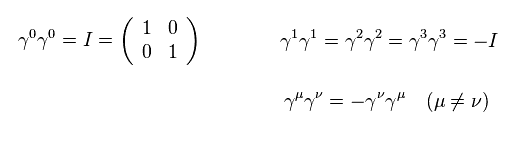
Here we introduced 4 × 1 Dirac spinor Ψ, as follows,
(Eq.4)
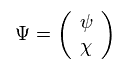
Dirac equation is
(Eq.5)
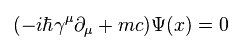
where
(Eq.6)
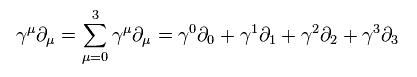
Here we use natural unit, so
(Eq.7)
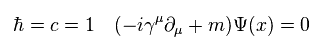
Multiplying Eq.7 by γ0 from left side,
(Eq.8)
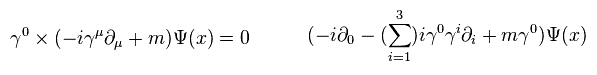
where
(Eq.9)
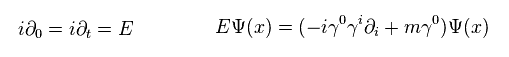
"E" means energy, which is the time derivative .
And the momentum operator (= p ) is
(Eq.10)
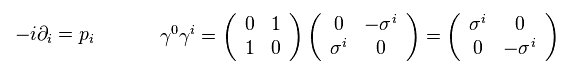
Using Eq.10 and Eq.4, Eq.9 becomes
(Eq.11)
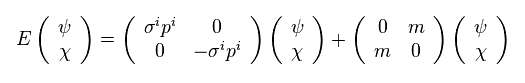
From Eq.11, we obtain two equations,
(Eq.12)
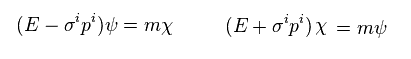
where
(Eq.13)
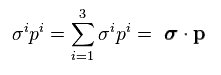
When fermion's mass is zero ( m = 0 ), Eq.12 becomes
(Eq.14)
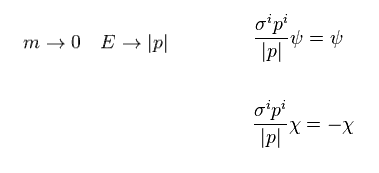
As you see Eq.14, upper 2 component spinor ψ has plus helicity (= σp ).
This means the directions of spin (= σ ) and momentum (= p ) are the same. (= right-handed ).
On the other hand, the lower 2 component spinor (= χ ) has minus helicity.
So this is left-handed spinor.
(Eq.15)
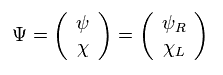
If we apply γ5 matrix on spinor, upper and lower spinors give different signs.
(Eq.16)
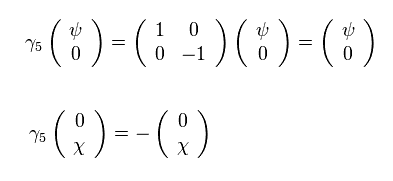
To make Dirac equation Lorentz invariant, they needed to define Lorentz transformation of spinor.
They introduced the following S operator.
(Eq.17)
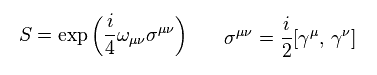
In Eq.17, ω is antisymmetric constant.
And σμν is commutator of two γ matrices.
( This σ is NOT Pauli matrix. )
(Eq.18)
So we have
(Eq.19)
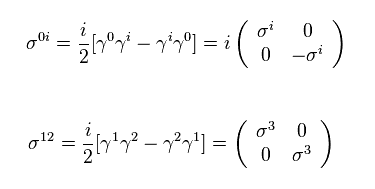
Using Eq.18 and Eq.19, infinitesimal Lorentz transformation of Eq.17 becomes
(Eq.20)
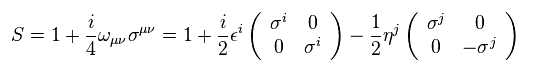
In Eq.20, we express ω using different constants ε and η
Applying Eq.20 Lorentz operator to Dirac spinor of Eq.15,
(Eq.21)
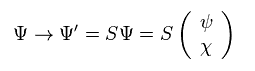
From Eq.20 and Eq.21, we have
(Eq.22)
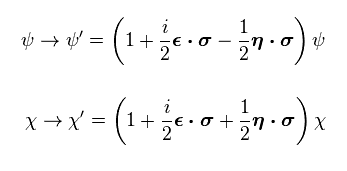
From Eq.20, the inverse matrix of Eq.20 is
(Eq.23)
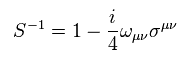
Because
(Eq.24)
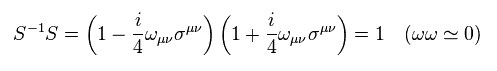
From Eq.1 and Eq.2, we have
(Eq.25)

From Eq.17, Eq.20, Eq.23, Eq.25 we obtain the following relation,
(Eq.26)
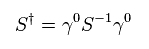
where we use
(Eq.27)
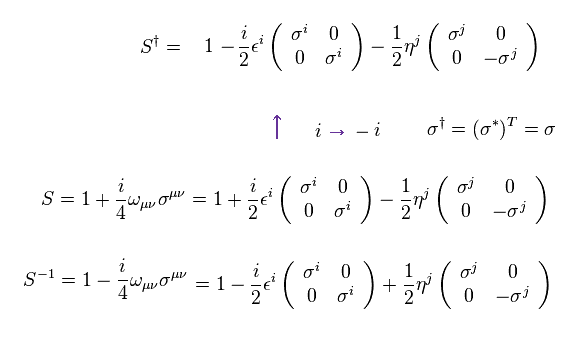
As a result,
(Eq.28)
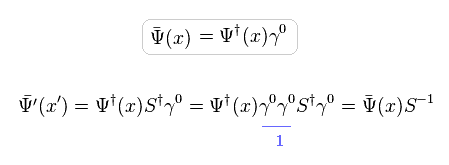
So, Dirac Lagrangian is invariant under Lorentz transformation (= S ), as follows,
(Eq.29)
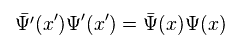
Like Eq.27, when we define
(Eq.30)
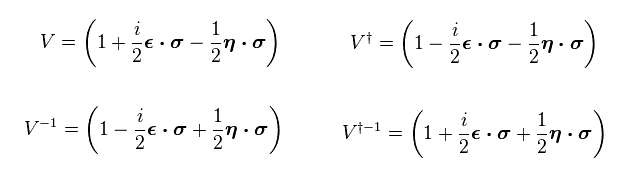
In Eq.30, Pauli matrices σ is Hermitian matix.
So the comlex conjugate transpose of σ remains the same ( σ† = σ ).
From Eq.22 and Eq.30, we have
(Eq.31)
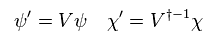
Lagrangian of Eq.29 can be expressed as
(Eq.32)
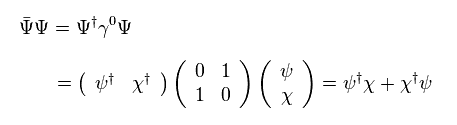
and
(Eq.33)
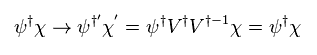
So, we can prove Eq.32 is scalar Lagrangian.
Here we use the notations of
(Eq.34)
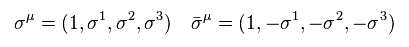
From Eq.30 and Eq.31, we have
(Eq.35)
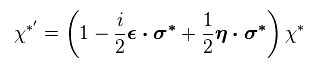
From Eq.2, each Pauli matrix satisfies
(Eq.36)
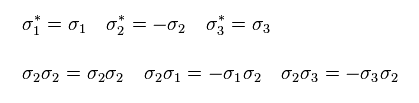
Because only σ2 consists of imaginary number.
From Eq.35 and Eq.36, we get
(Eq.37)
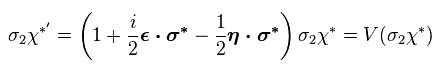
Eq.37 means this wavefunction transforms like ψ of Eq.31, as follows,
(Eq.38)
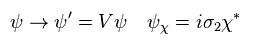
Like Eq.33,
(Eq.39)
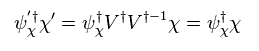
Using Eq.38, Eq.39 becomes
(Eq.40)
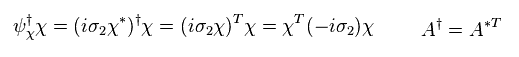
In Eq.40, i* = -i, and σ2* =- σ2 is used.
And
(Eq.41)
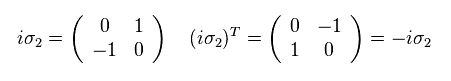
From Eq.41,
(Eq.42)
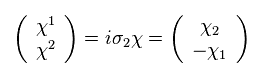
Here we define
(Eq.43)
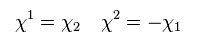
From Eq.42 and Eq.43,
(Eq.44)
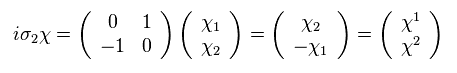
(Eq.45)
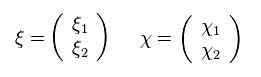
From Eq.44 and Eq.45,
(Eq.46)
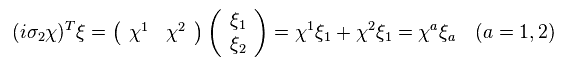
Using Eq.44, Eq.46 becomes
(Eq.47)
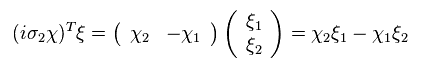
E.47 is Lorentz invariant scalar.
χ and ξ are fermions, so anticommutator of Eq.47 isn't zero.
Here we introduce new operator of εab,
From Eq.43 and Eq.44, we have
(Eq.48)
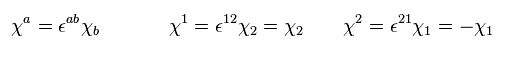
So,
(Eq.49)
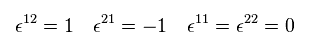
Eq.48 is equal to
(Eq.50)
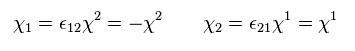
So,
(Eq.51)
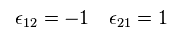
Using Eq.49, we can express
(Eq.52)
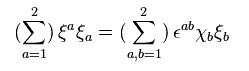
Under the external electromagnetic field, Dirac equation contains vector ( scalar ) potentials A, like
(Eq.53)
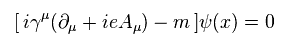
The complex conjugate (= * ) of Eq.53 is
(Eq.54)
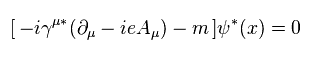
Using Eq.1 and Eq.3, we get the relation of
(Eq.55)
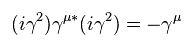
Because,
(Eq.56)
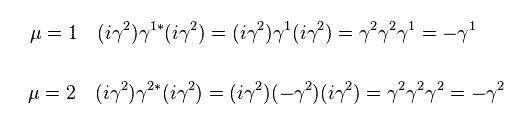
Multiplying Eq.54 by ( iγ2 ) from left side,
(Eq.57)
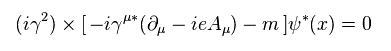
The first term of Eq.57 can be expressed as
(Eq.58)
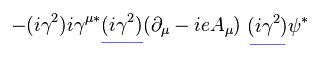
where we insert
(Eq.59)
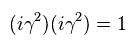
Using Eq.55 and Eq.58, Eq.57 becomes
(Eq.60)
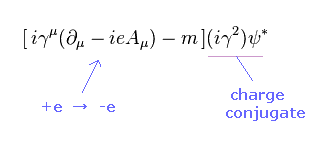
Comparing Eq.53 and Eq.60, you find the charge "e" of Eq.60 becomes the opposite from Eq.53.
(= Charge conjugate of ψ becomes iγ2ψ*. Just artificial rule. )
When we define
(Eq.61)
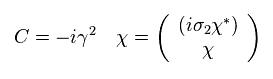
We get
(Eq.62)
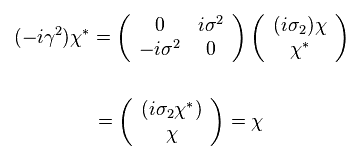
This means, when the form of the spinor is Eq.61, the charge conjugate of wavefunction is equal to the original one.
The charge conjugate is antiparticle, so in this case, the particle is the same as its antiparticle.
(Eq.63) Majorana particle ?
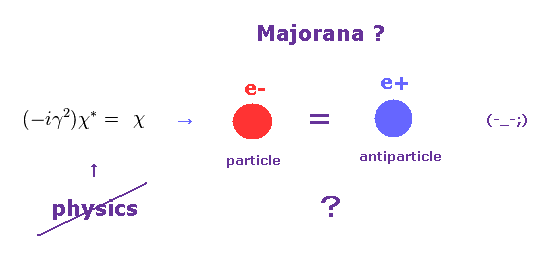
They call this state Majorana particle.
It is said that neutrino and photino are Majorana fermions.
But unfortunately, this is just abstract math operator, lacks physical images.
(Eq.64) Supersymmetry Lagrangian ?
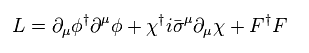
Eq.64 is the simplist supersymmetry Lagrangian (= Wess-Zumino model ).
φ is boson, and χ is fermion ( here we consider simple Majorana fermion ).
And "F" is "unreal" auxiliary field (= boson ), which is indispensable for supersymmetry algebra.
These auxiliary fields were artificially introduced, which proves supersymmetry itself is just math ( NOT physical ) concept.
(Eq.12)
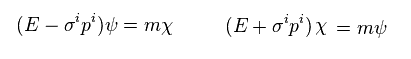
From the right Dirac equation of Eq.12, we have
(Eq.65)
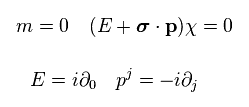
this is
(Eq.66)
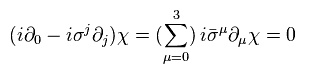
where we use
(Eq.34)
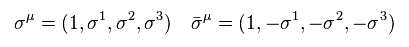
As shown on this site (p.33), units of total Lagrangian (= L ), boson (= φ ), fermion (= χ ), and F boson become
(Eq.67)
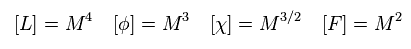
here we use the natural unit of
(Eq.68)
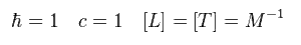
They define supersymmetric transformation of boson φ as
(Eq.69)
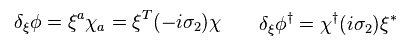
Of course, boson is NOT fermion.
So two fermions (= ξ, χ ) are necessary for expressing one boson (= φ ).
From Eq.67 and Eq.69, the unit of this strange fermion ξ is
(Eq.70)
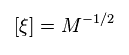
So, this ξ is completely different from the ordinary fermion χ of Eq.67.
Depending on these unreal fermions and bosons proves supersymmetry itself is NOT truth.
(Eq.71)
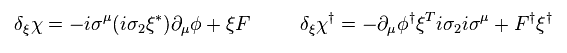
And they define supersymmetry transformation of fermion χ (= Eq.71 ) and boson F (= Eq.72 ).
Of course, these forms were artificially introduced, and NOT natural ones.
(Eq.72)
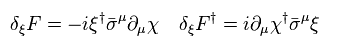
Transformation of boson part in Lagrangian (= firs term of Eq.64 ) becomes
(Eq.73)
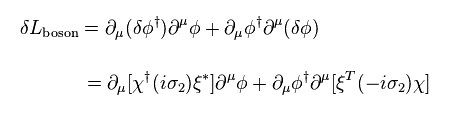
In Eq.73, Eq.69 is inserted.
From Eq.64 and Eq.71, fermion's transformation becomes
(Eq.74)
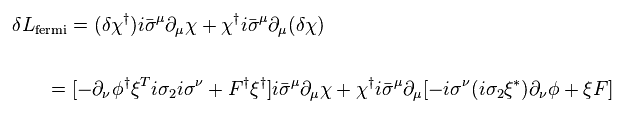
Here we use the antisymmetric property of Pauli matrices.
And integration by parts gives negative sign.
(Eq.75)
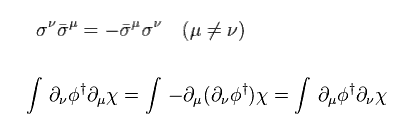
Using Eq.36,
(Eq.76)
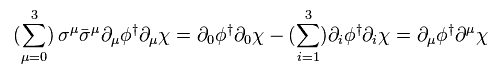
As a result, Eq.74 becomes
(Eq.77)
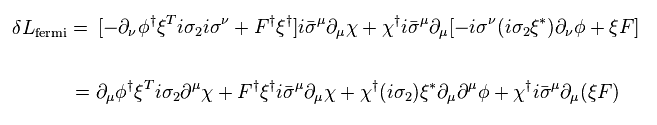
Again, the integration by parts gives negative sign, as follows,
(Eq.78)
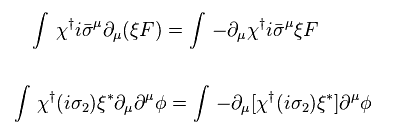
Using Eq.72, auxiliary parts FF transforms like
(Eq.79)
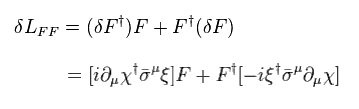
From Eq.73, Eq.77 and Eq.79, the change of total Lagrangian becomes zero,
(Eq.80)
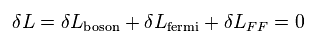
Eq.80 means Lagrangian of Eq.64 is invariant under supersymmetric transformations of Eq.69, Eq.71 and Eq.72.
This is called "supersymmetry".
You find physicists try to define artificial rules, and make Lagrangian invariant by force under supersymmetry transformation.
So SUSY does NOT mean the law of Nature at all, it exists only inside math equation.
Basically, Lagrangian of MSSM (= minimal supersymmetric standard model ) becomes
(Eq.81)
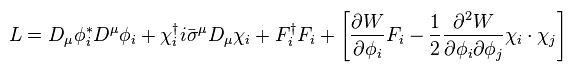
The last term of Eq.81 is potential energy.
And "D" is covariant derivative.
(Eq.82)
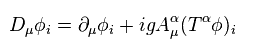
In Eq.82, A is vector potential, or gauge bosons.
Due to the strict limitation of SUSY and Lorentz invariance, the form of W must be
(Eq.83)
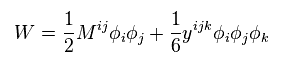
Furthermore we can add the Lagrangian of vector potential ( ex. photon ),
(Eq.84)
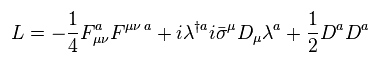
λ of Eq.84 is "photino". Just math ( NOT physical ) symbols.
And antisymmetric tensor of Eq.84 is
(Eq.85)
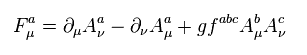
The interactive Hamiltonian between Higgs (= H ) and other particles are
(Eq.86)
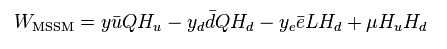
Eq.86 gives "mass" to particles including Higgs itself.
As supersymmetry must be broken, the mass Lagrangian of SUSY particles is
(Eq.87)
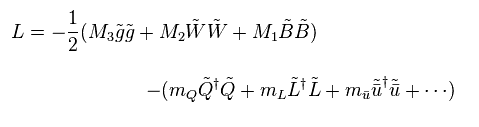
Due to this SUSY breaking, as many as 124 free parameters appear even in MSSM.
So supersymmetry cannot predict anyhing at all.
MSSM define R parity.
Of course, this R parity is just artificial rule, NOT a natural result.
(Eq.88)
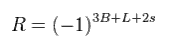
Ordinary particles always have R = +1, and SUSY particles have R = -1.
For example, in ordinary quark, B (= baryon ) number is 1/3, L (= lepton ) number is zero,
and spin S is 1/2.
(Eq.89)
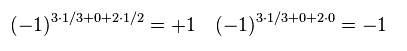
The left of Eq.89 is R parity of ordinary quark, and the right of Eq.89 is squark.
Spin S of squark is zero, so R parity becomes -1.
The current useless quantum field theory considers ONLY invariance of Lagrangian L ( or action S ) under some transformation.
The variation of action S is expressed as
(Eq.90)
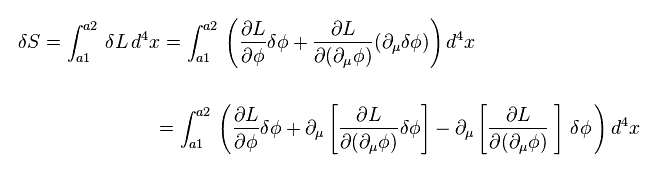
Here we use Euler-Lagrange equation of
(Eq.91)
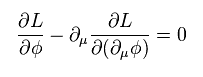
Eq.90 becomes
(Eq.92)
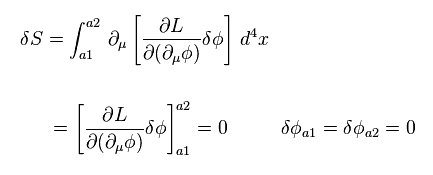
Integral of total derivative becomes zero, as shown in Eq.90.
This means, when Euler-Lagrange equation holds, action S is invariant under some transformation.
If we define artificial current J as
(Eq.93)
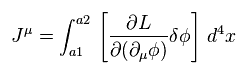
Eq.92 can be expressed as
(Eq.94)
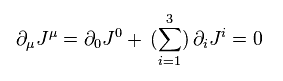
Eq.94 means, if we define artificial charge Q as
(Eq.95)
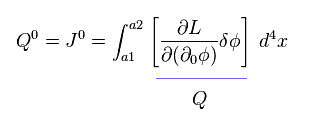
This total charge is conserved.
SUSY theorists considers this unreal charge Q as most imporntant concept. This is strange.
Generally, arbitrary transformation can be expressed using this charge Q, as follows,
(Eq.96)
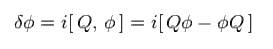
Here we use Lagrangian of
(Eq.64)
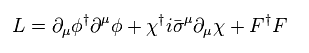
The canonical momentum π of boson field φ is
(Eq.97)
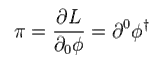
Here we define commutation relation between this φ and its canonical momentum (= π ).
(Eq.98)
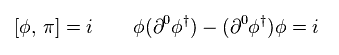
From Eq.95 and Eq.64, the charge Q becomes
(Eq.99)
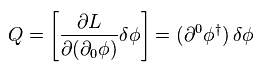
Using Eq.98 and Eq.99, we have
(Eq.100)
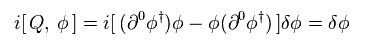
We can prove Eq.96.
(Eq.101)
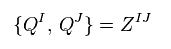
When there are several kinds of transformations (= Q ), the anticommutator of these Q give the central charge Z of Eq.101.
To cancel this abstract central charge, superstring theory needs unreal 10 dimensions, as shown on this page.
So there are NO physical reality in these SUSY and string theory.
They are just math symbols.
Basicaly, rotational operator can be expressed as
(Eq.102)
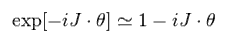
"J" is angular momentum, and θ is angle.
In case of spinor rotation, J becomes Pauli matrices (= σ/2 ),
(Eq.103)
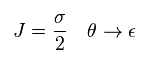
Charge "Q" of SUSY is a spinor, so it changes like
(Eq.104)
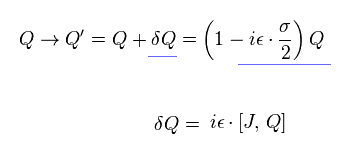
If we define
(Eq.105)
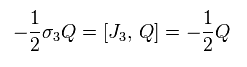
we have
(Eq.106)
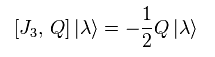
and
(Eq.107)
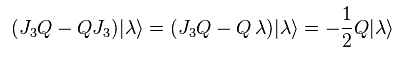
As a result,
(Eq.108)
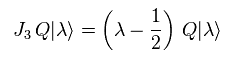
Eq.108 means the charge Q can decrease particle's spin 1/2.
But SUSY theorists NEVER try to say what this charge Q ( = spin stropper !? ) really is.
(Eq.109)
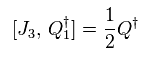
In case of complex comjugate of Q,
(Eq.110)
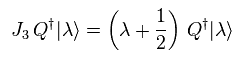
Spin 1/2 is increased.
(Eq.111)
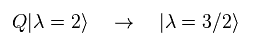
If this charge Q is applied to graviton with spin "2", it changes into gravitino with spin 3/2, they insist.
Unfortunately, there are NO other concrete explanations about spin here.
(Eq.112)
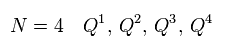
When there are 4 kinds of supersymmetric transformation, this is called "N=4" supersymmetry.
In this case, the number of different Q is "4".

2014/5/1 updated. Feel free to link to this site.