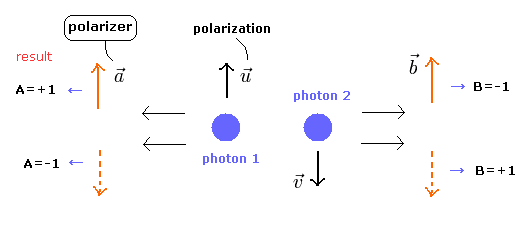
ここでは、 u, v, a, b のベクトルはすべて 単位ベクトルである。
トップページ (2電子原子も含む正確な新ボーア模型)
ボーアモデル vs. ベルの不等式の破れ (CHSH-type)
アスペによるベルの不等式の破れの実験により、局所実在性 (local realism, local hidden-variable) が否定されたとされている。
後に、Leggett が 非局所的な隠れた変数理論 (= non-local hidden variable realism) を提唱し、しかもこれがベルの不等式 (CHSH-type) を破る可能性を示した。
しかし、彼の Leggett-type 不等式も、最近の実験 (Nature 446,871,(2007)) によって否定された。
重要な点は、これらの実験は "非実在の" 光子という粒子を使っているという点だ。
もし、光子という粒子の代わりに 単純な 電磁波モデルを使うと、量子力学的な実験結果と合う 局所実在性の模型を何と表わすことが可能なのだ。 ( このページ を参照のこと。 )
ところで、この Leggett-type の不等式とは何なのだろうか?
彼の理論は本当に 非局所的でかつ 実在的なものなのだろうか?
実は、Leggett-type 模型には 致命的な欠陥 が存在する。
その欠陥についてここでは詳しく述べることにしよう。
最初に、互いに反平行の偏光軸 ( = polarization, u と v, v = -u ) をもつ、エンタングルした(もつれた)光子のペア (1 と 2) を想定する。
Fig.1 エンタングルした光子のペアと偏光板 (polarizer)。

ここでは、 u, v, a, b のベクトルはすべて 単位ベクトルである。
Fig.1 に示すように、光子1は偏光板 a、光子2は偏光板 b に向かっている。
もし、偏光板 a と u の偏光軸が 平行 ( a = u ) のとき、通過する光子の振幅 (ここでは確率密度でなく振幅を使う)は、A= +1 となる。
(もし、これらが”反平行”のときは、A は -1 となる。)
Malus' law によれば、通過する光の振幅は、cosθ (θ は光子の偏光軸と偏光板の角度) となる。
Leggett's 模型では、非局所的な隠れた変数 (= λ) が許される。
これはすなわち、偏光板 a の情報が ”超光速で”瞬時に 偏光板 b に伝わることを意味する。
しかし、この模型は”現実性 = realism ”を満足するというのである。
はたしてこんなことが可能なのだろうか?
Leggett 模型では、偏光板 a の 結果 A が次のようになるとされる。
(Eq.1)
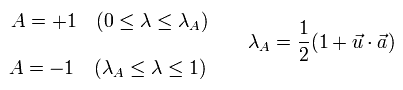
例えば、ベクトル u と a が互いに 平行 のとき、 u と a の内積は +1 になる。
すると、λA は 1 となり、結果 A は 必ず +1 となる。
もし、ベクトル u と a が 反平行のときは、u と a の内積は -1 となる。
つまり、λA は 0 となり、このとき 結果 A は 必ず -1 になる。
また、偏光板 b の 結果 B は次のようになる。
(Eq.2)
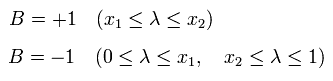
ここでは これらの x1 と x2 は次の条件を満たすとする。
(Eq.3)
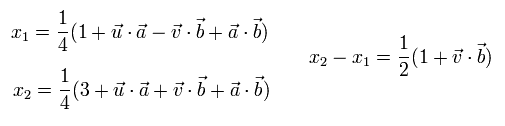
Eq.3 は、偏光板 b の結果 B は ”超光速で瞬時に”、結果 A の影響を受ける ことを意味する。
なぜなら これらの x には、u と a の内積が含まれているからである。
ここでは、互いにエンタングルした光子1と2の偏光軸は、次のように互いに反平行とする。
(Eq.4)
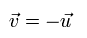
この奇妙な非局所変数 λ を使うと、結果 A と B の平均はそれぞれ次のようになる。
(Eq.5)
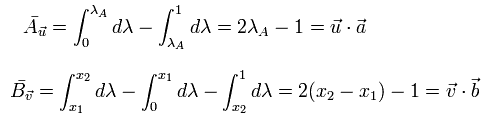
驚くことに、Eq.5 に示すように、Leggett's 模型は 各光子ごとに Malus's law を満たすのである。
明白な偏光軸を持つ各光子 (= realism) が 独立して Malus's law をみたす。しかし一方で その光子は CHSH-type のベルの不等式を破る (Eq.6)。
こんなことが果たして可能なのだろうか!?
( CHSH-type のベルの不等式に関しての詳細は、このページを参照のこと。)
( Eq.6. AとBを組み合わせた結果の平均の値。 )
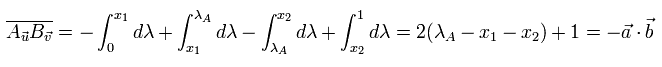
例えば、 第1項では、0 < λ < x1 の場合で、この時 AB = +1 (=A) × -1 (=B) = -1 となる。 (Eq.1 と Eq.2 を参照のこと。)
Eq.6 は、光子1が偏光板 a を通過したとたんに 光子2の偏光軸が 偏光板 a と同じ (=反平行) になることを意味する。(=エンタングルメント。このページも参照のこと。)
実は、この驚くべき現象は、Leggett's 模型の 致命的な欠陥を隠すことによってのみ可能なのである。
最初に Eq.2 の条件が満たされるとしたら、x1 と x2 は次の条件を満たさなければならない。
(Eq.7)
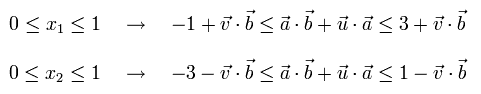
Eq.7 の制限は、 Eq.8 と同じ意味である。
(Eq.8)
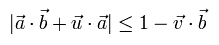
Eq.6 は次の制限も含んでいる。
(Eq.9)
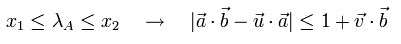
Eq.8 と Eq.9 を組み合わせて、Leggett モデルは、次の重要な条件を満たさなければならない。
(Eq.10)
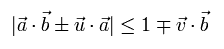
Eq.10 が 実は、非局所かつ現実性の Leggett 模型が 驚くべき幻想を引き起こす諸悪の根源なのである。
例えば、偏光板 a と b の方向が次のように 同じとき、
(Eq.11)
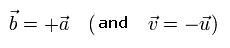
x1 と x2 はそれぞれ次のようになる。
(Eq.12)
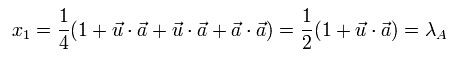
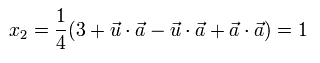
Eq.1, Eq.2, Eq.12 より、AとBの結果は、共通の非局所パラメーター λ に応じて、次のようになる。
(Eq.13)
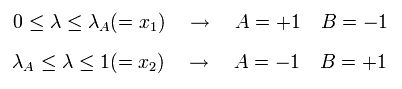
Eq.13 によれば、AとBの結果は 必ず正反対 (=反平行という意味) になり、これはすなわち 光子1と2がエンタングルメントを引き起こしていることを意味する。
Eq.13 は、Fig.2 に示す 我々の 電磁波モデル に相当するケースである。
Fig.2. 電磁波モデル (= 局所かつ実在的なモデル)。
(ここでは、振幅のかわりに確率”密度”を使っているが、意味は同じである。)
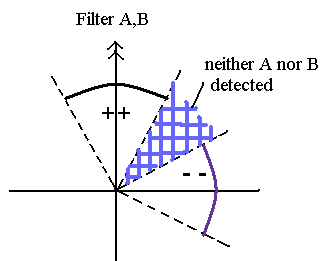
また、ここでは、光子1、2は光子A、Bと表示している。偏光板 a と b は、Filter A、Bと表示している。
この図は、偏光フィルターA (=a) と B (=b) の角度(矢印の示す方向)が同じ場合だ ( = 0°)。
前に言ったように、光子1 (= A) と 2 (=B) は正反対の偏光軸(つまり互いに反平行な軸)を持つ。つまり、この場合は、光子AがフィルターAを通過したとき、光子Bも必ず フィルターBを通過する。( = cos2 0 = 1)
光子1の(=光子2も同じ)偏光軸がこの図の ( ++ ) の方向を向いているとき、光子1と2両方が各フィルターを通過し、光子として検出することができる。
しかし、光子1(=光子2)の偏光軸がこの図の青の部分を向いているとき、通過(もしくは反射)する両光子1、2の光の強さは検出閾値以下であり、光子1も2も検出器で”光子”として検出することができない。(この場合は検出効率の計算にも使用されない。)
また、光子の偏光軸が図の ( - - ) の方向を向くとき、両光子1,2とも十分に反射され、光子として検出することができる。
つまり、この場合もペア光子の”エンタングルメントという幻想”が起こっており、これを我々の電磁波モデルは再現することが可能なのである。
では、Fig.3 の場合はどうなのであろうか?
(Fig. 3)
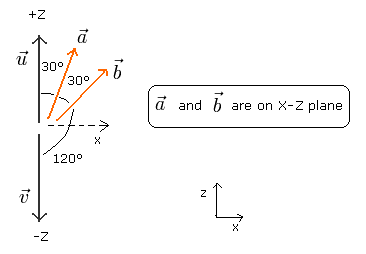
ここでは、光子1の偏光軸 u と 偏光板 a の間の角度が 30° であり、また光子2の偏光軸 v と 偏光板 b の角度が 120° の場合である。
Fig.3 のすべてのベクトルを Eq.8 に代入すると、何と 次のような おかしな不等式が得られてしまう。
(Eq.14)
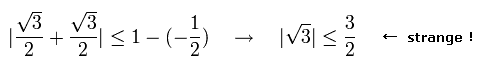
Eq.14 の不等式は現実にはみたすことはできない。
これが、Leggett's 模型の 幻想を引き起こす根源 である。
つまり、ある角度では、Leggett 理論は 破綻してしまい、これによって ある状況で 非局所実在論 が否定されてしまうことになる。
もちろん、 このページに示したように、我々の 電磁波モデル は Fig.3 の状況でも説明可能である。これは "local realistic" なモデルにも関わらず大丈夫なのだ。
Fig. 4. 電磁波モデル (= 局所かつ実在的なモデル)。
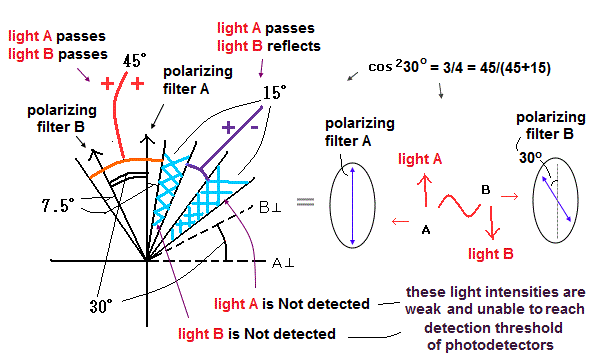
赤い部分 ( + + ) ----- 光子1と2両方とも各フィルターを通過し、検出される。
紫の部分 ( + - ) ----- 光子1は通過し、光子2は反射し、両方とも検出される。
斜線部分 ( 水色 ) ---- 光子1のみ ( 通過 ) か、 光子2のみ ( 反射 ) を光子として検出できる。(=この場合は正しい実験結果として使われない。)
基本的に、もし 次の Eq.15 の条件が満たされれば、Leggett 模型は Eq.10 の制限に矛盾しなくなる。
(Eq.15)
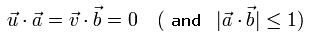
(Eq.15 を Eq.10 に代入してみるといい。)
Eq.15 の条件が満たされるとき、各ベクトルの方向は次の図に示すようになる。
(Fig. 5)
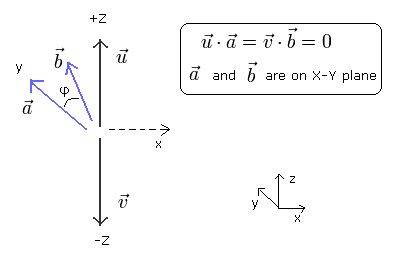
ここでは、偏光板 a と b は x-y 平面にあるため、それらは 光子のベクトル u と v に垂直である。
Fig.5 では、a と b の間の 任意の角度 (φ) において、Leggett 模型は CHSH-type のベルの不等式を破ることができる。なぜなら、Eq.10 が必ず満たされているからである。
しかし、Fig.5 の状況は とても不自然に 私にはみえるのだが・・。
次に、Leggett-type の不等式を導出する。
AとBのいかなる組みあわせ (A= ± 1, B= ± 1) においても 、次の式が成り立つ。
(Eq.16)
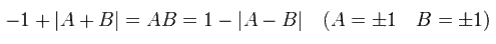
Eq.16 の平均は次のようになる。
(Eq.17)
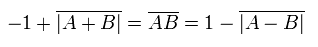
また、これより次の不等式が成り立つ。
(Eq.18)
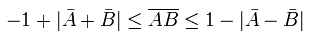
ここで、”定まった”偏光軸を持つ各光子 (=realism) ごとに、Malus' law を使う。
(Eq.19)
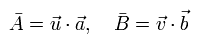
上ですでに述べたように、この置き換えは、ある角度 φ において 量子力学的な結果と一致しない。
Eq.19 を Eq.18 に代入する。
(Eq.20)
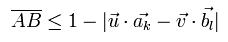
ここで、k と l は偏光板の番号を表している。(この実験では、いくつかの異なる偏光板が必要である。)
すると、いろんな偏光軸 u と v の光子群を平均したものは、次のようになる。
(Eq.21)
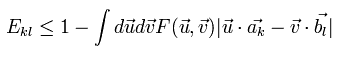
Fig.5 と Eq.15 で述べたように、もし 1平面のみに存在する偏光板を使用すると、Leggett's 模型は CHSH-type の ベルの不等式を破ることが可能である。
そのため、次のような 異なる平面 (x-y と x-z) に存在する偏光板を使う必要がある。
Fig. 6. ポアンカレ球における 3次元の偏光板。
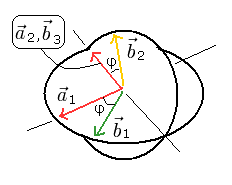
ここでは、偏光板 a2 は b3 と同じである。
偏光板 a1 と b1 の間の角度は φ である。
また、偏光板 a2 と b2 の間の角度も φ である。
(a1 と b1 は、x-y 平面にあり、 a2 と b2 は x-z 平面にある。)
もし、Fig.6 の偏光板を使うと、Eq.21 の 4つの Ekl の合計は、次のようになる。
(これには長い計算をする必要がある。詳細はこの論文 (arXiv 0704.2529v2) を参照のこと。)
( Eq.22. Leggett-type の不等式。 )
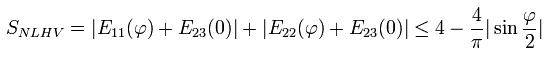
もし、ここで量子力学的な関係を考慮すると、Fig.6 の 各 Ekl は次のようになる。
(Eq.23)
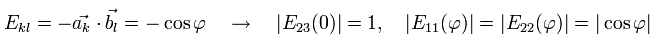
つまり、量子力学的な状況では、Eq.22 の Leggett 不等式は、Eq.24 の形に変化する。
(Eq.24)
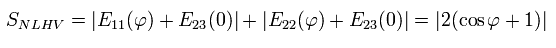
実験では、ある角度 φ において、Eq.22 の Leggett の不等式は 破られる。
(実験結果は Eq.24 と同じになる。)
Eq.22 の Leggett の不等式と Eq.24 の量子力学的な等式の違いは、Eq.19 (=realism) の置き換えに起因する。
上ですでに述べたように、もし Eq.5 と Eq.19 の ”明確な偏光角を持つ光子” という実在性を利用しようとすると、Eq.10 の とても厳しい制限を満たさなければならない。
この Eq.10 の制限は厳しすぎるため、ある角度 φ においては満たすことができない。(例えば、Fig.3)
結果として、Leggett-type の不等式 (Eq.22) は、量子力学的な等式 (Eq.24) と同じにはならない。
つまり、最初から、”不完全な”Leggett 模型は 不可能なこと (=エンタングルメント+実在性+光子) をしようとしていたわけである。
最近では、光の軌道角運動量 (これは、偏光と似たようなものである) を用いて、Leggett-type の不等式が破られたことが実験で示された。
(New Journal of Physics 12 (2010) 123007).
これはすなわち、ド・ブロイ・ボーム解釈 (de Broglie Bohm's theory) を含む 非局所実在モデルが否定されたことを意味する。
それで、彼らは 量子力学には何のリアリティーもなくなった と主張しているのである!
これは、この世界が単なる 幻想 の産物だということであろうか!?
これらの奇妙な結果は 実は 光子が実在の粒子だというそもそもの誤解 から生じている。
もし、光子が”実在の”粒子だとしたら、Fig.7 に示すような 1光子が自分自身と干渉できるのであろうか ??
Fig.7. マッハ・ツエンダー干渉計。
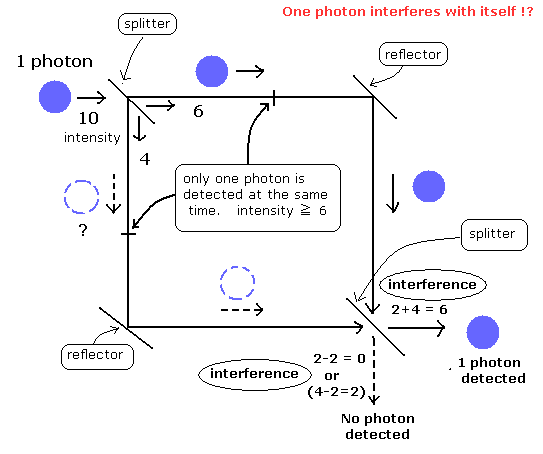
このページに示したように、電磁波モデルはこの単一光子の干渉実験を 正しく、かつ自然に説明することができる。
もし、光子が”実在の”粒子だったら、1つの光子が 2つの経路に分離することができるのだろうか ??
たとえ、仮に 単一光子が”分離”できたとしても、干渉そのものの現象は電磁波としての波の性質でないと説明できない。
”複雑な”エンタングルメントの実験を考慮する前に、光子そのものに実在性がないのである。
この事実が、エンタングルメントの実験が 局所的(もしくは非局所的)な実在世界を否定した という 幻想 を生じさせてしまった。
”Quantum physics says goodbye to reality” と主張するかわりに、我々は、量子力学に goodbye というべきであろう。

2011/1/1 updated This site is link free.