斀揮朄偵傛傞嶼妟栤戣
丂丂丂丂丂丂丂丂丂丂丂 丂丂亂怴彑帥妟摪偵曭擺偝傟偨嶼妟偺栤戣亃
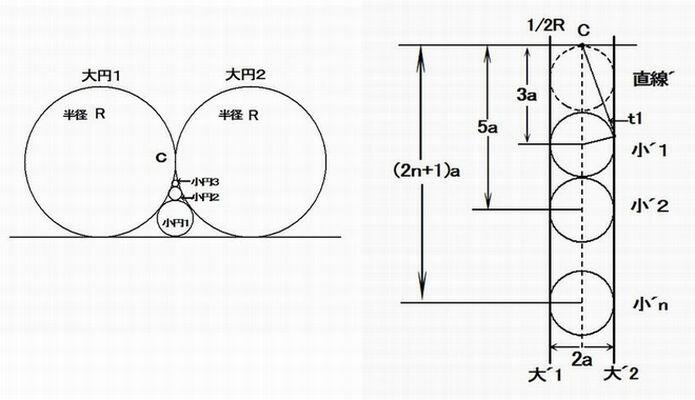
敿宎 R 偺俀屄偺戝墌偲偦傟偵愙偡傞捈慄偲偺娫偵彫墌傪拃師擖傟偰峴偔丅嵟弶偺彫墌傪戞1墌偲偡傞偲偒
値斣栚偺敿宎 r(n) 傪媮傔傛丅
丂丂亂斀揮朄偵傛傞夝朄亃
摍偟偄戝墌偳偆偟偺愙揰 C 偱斀揮偡傞偲塃偺斀揮恾偲側傞丅
斀揮憸偺彫丩墌偺敿宎傪 倎 偲偡傞偲丂丂倎 = 1/(2R) 丒丒丒嘆
C 偐傜奺彫丩墌傊偺愙慄偺挿偝丂倲値 偼丂
倲1^2 = (3倎)^2 - 倎^2
倲2^2 = (5倎)^2 - 倎^2
丒
丂丂丂丂丂丒
倲値^2 = ((2値+1)倎)^2 - 倎^2
斀揮婎杮幃偱丄墌宎偵敿宎傪梡偄傞偲 r = (1/(t^2))倎
丂
r1 = 倎/((3倎)^2 - 倎^2)
r2 = 倎/((5倎)^2 - 倎^2)
丒
丂丂丂丂丂丒
倰値 = 倎/(((2値+1)倎)^2 - 倎^2) = 1/((4値^2 + 4値)倎) = 2R/4値(値 + 1)
丂亪丂値 斣栚偺彫墌敿宎偼丂丂 倰値 = R/2値(値 + 1) 偱偁傞丅
丂丂丂丂丂丂丂丂丂丂亂 嫗搒丒杒栰揤枮媨偵曭擺偝傟偨嶼妟偺栤戣丒丒丒嶼妟偼尰懚偟偰偄傑偣傫 亃
亂栤戣亃
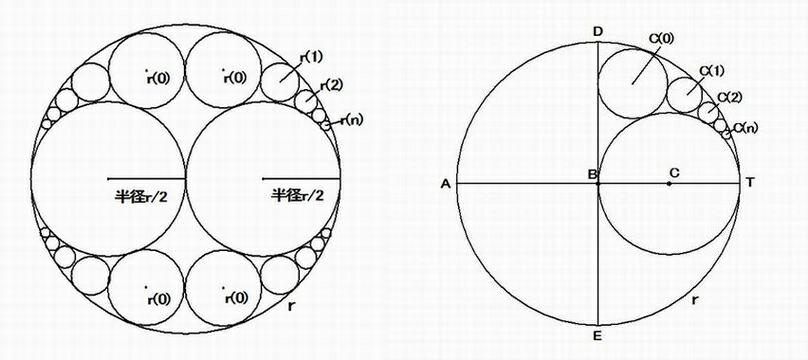
壓偺恾 偵帵偡傛偆偵丄懳徧揑偵4偮偺摨偠戝偒偝偺敿宎偺墌偺嵔乮偔偝傝乯乷r(k) 乸( k= 0, 1, 2, 丒丒丒, n) 偑敿宎 r/2 偺2偮偺墌偵奜愙偟丄
敿宎 r 偺戝墌偵撪愙偟偰偄傞丅偙偺偲偒 r(n) 偼丄偮偓偺傛偆偵昞偝傟傞偙偲傪徹柧偣傛丅
丂丂丂丂丂丂丂丂丂丂丂丂r(n) = r / { n(n亄2併2)亄4 }
亂恾侾丗嶼妟偺恾(尰戙梡)亃 丂 亂恾俀丗娙棯恾亃
揰B 偼嵟弶偺戝墌偺拞怱偱偦偺敿宎偼r 丄 揰C 偼敿宎 r/2 偺墌偺拞怱偱偡丅傑偨丄揰C(k) ( k= 0,1, 2, 丒丒丒, n ) 偼楢懕揑偵奜愙偡傞墌偺拞怱偱丄
偦偺敿宎偼r(n) 偱偡丅
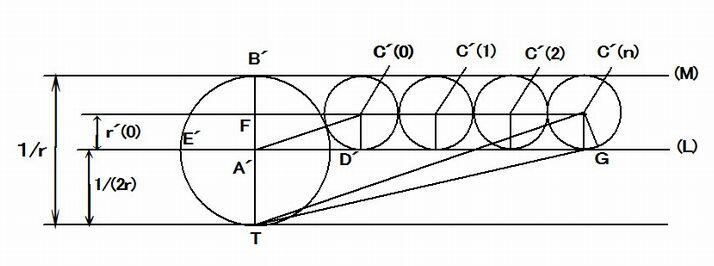
亂恾俁丗娙棯恾偺斀揮恾亃
丂娙棯恾偺斀揮恾 偼丄偮偓偺傛偆偵峔惉偝傟偰偄傞丅
(a) TA=2r , TAA' = k^2, k亖1 偐傜 TA' = 1/TA = 1/(2r) 偱偁傞丅偟偨偑偭偰丄亂恾俀亃偺斀揮偺拞怱T 傪捠傝丄
捈宎TA=2r 偺戝墌偼丄亂恾俁亃偱偼丄揰A' 傪捠傝丄TA' 偵悅捈側捈慄 乮L乯 偵斀揮偝傟偰偄傞丅
(b)丂摨條偵偟偰丄TB=r , TB' = 1/TB = 1/r 偱偁傞偙偲偐傜丄 亂恾俀亃偺斀揮偺拞怱T 傪捠傞丄捈宎TB=r 偺墌偼丄
丂丂亂恾俁亃偱偼丄揰B' 傪捠傝丄TB' 偵悅捈側捈慄 乮M乯偵斀揮偝傟偰偄傞丅
(c)丂忋婰偺嘆偲嘇偱帵偟偨俀捈慄 乮L乯 偲乮M乯 偼暯峴偱偁傞丅
(d) 亂恾俀亃偺斀揮偺拞怱T 傪捠傜側偄慄暘DBE偼丄亂恾俁亃偱偼丄慄暘TB' 傪捈宎偲偡傞墌偺敿墌晹暘D'B'E' 偵
丂丂斀揮偝傟偰偄傞丅
(e)丂亂恾俀亃偺揰C(0) 傪拞怱偲偡傞墌偼丄敿宎 r 偺戝墌偵撪愙偟丄敿宎 r/2 偺墌偵奜愙偟丄慄暘DBE偵愙偟偰偄傞偙偲
丂丂偐傜丄揰C(0) 傪拞怱偲偡傞墌偺斀揮偼丄亂恾俁亃偱偼丄2捈慄 乮L乯, 乮M乯 偵愙偡傞丄揰C'(0) 傪拞怱偲偡傞墌偱偁傞丅
(f) 亂恾俀亃偺揰C(1) 傪拞怱偲偡傞墌偼丄敿宎 r 偺戝墌偵撪愙偟丄敿宎 r/2 偺墌偵奜愙偟丄揰C(1) 傪拞怱偲偡傞墌偵
丂丂奜愙偟偰偄傞偙偲偐傜丄 揰C(1) 傪拞怱偲偡傞墌偺斀揮偼丄 亂恾俁亃偱偼丄揰C(1) 傪拞怱偲偡傞墌偵奜愙偟丄暯峴側
丂丂2捈慄 乮L乯, 乮M乯偵傕愙偡傞丄揰C乫(1) 傪拞怱偲偡傞墌偱偁傞丅
(g)丂忋婰偺嘍偲嘐偐傜丄亂恾俁亃偺揰C'(i) ( i = 0, 1, 2, 3, 乧, n ) 傪拞怱偲偡傞丄楢懕揑偵奜愙偡傞墌偺敿宎偼
丂丂r'(i) ( i = 0, 1, 2, 3, 乧, n ) 偼偡傋偰摍偟偄丅
丂 偡側傢偪 r'(0) = r'(1) = r'(2)= 丒丒丒 =丂r'(n)丂偑惉傝棫偮丅丂
丂亂恾俁亃偵偍偄偰 A'C'(0) = 2丒r'(0) + r'(0) = 3丒r'(0) 偟偨偑偭偰 仮A'FC'(0) 偱
FC'(0)^2 = A'C'(0)'^2亅A'F^2 = (3丒r'(0))^2亅r'(0)^2丂= 8丒r'(0)^2 傛偭偰丂FC'(0) = 2併2丒r'(0)
丂偙偙偱丄 r'(0) = r'(1) = r'(2) = 丒丒丒 = r'(n) 偱偁傞偐傜
丂FC'(n) = FC'(0)亄C'(0)C'(n) = 2併2丒r'(0)亄2n丒r'(0) = 2(n亄併2)丒r'(0)
丂偟偨偑偭偰 仮TFC'(n) 偱丂
(TC'(n))^2 = TF^2亄(FC'(n))^2 = (3丒r'(0))^2亄4(n亄併2)^2丒r'(0)^2 = 9丒r'(0)^2亄4(n亄併2)^2丒r'(0)^2
丂傛偭偰 仮TGC'(n) 偱 TG = L 偲偍偔偲丄 C'(n)G亖倰乫(n)=r(0) 偐傜
L^2 = TC'(n)'^2亅C'(n)G^2 = 乷9丒r'(0)^2亄4(n亄併2)^2丒r'(0)^2乸亅 r'(0)^2
= 8丒r'(0)^2 亄4(n亄併2)^2丒r'(0)^2 = 乷(n亄併2)^2亄2乸丒4r'(0)^2
丂偙偙偱丄丂2丒r'(0) = A'B' = TB' 亅 TA' = 1/r 亅 1/2丒r = 1/2丒r 偐傜 r'(0) = 1/4丒r
丂備偊偵丄慜愡偱帵偟偨亂掕棟D亃偵傛偭偰
r(n) = r'(n) / L^2 = r'(0) / {(n+併2)^2+2}丒4r'(0)^2 = 1/ { (n+併2)^2+2 }丒4r'(0) = r / { n(n+2併2)+4 }