【文化元年(1804年) に堀池六太夫が備中国（現・岡山県）の吉備津宮（現・吉備津神社）に掲げた算額 】

　 

 【現代風の要訳】

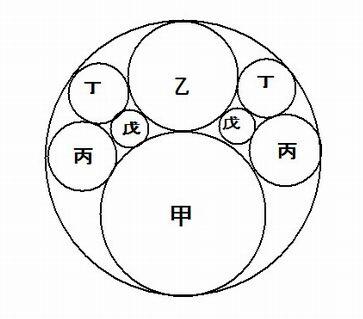
 図のように、大円内に甲円、乙円を各１個入れ、丙、丁、戊 の３円を左右に、各２個入れる。

甲円、乙円の直径を、それぞれ a 、b とするとき、戊円の直径は

　　　　　　　　　　ab(a + b)／(2a^2 + 3ab + 2b^2) と表されることを証明せよ。

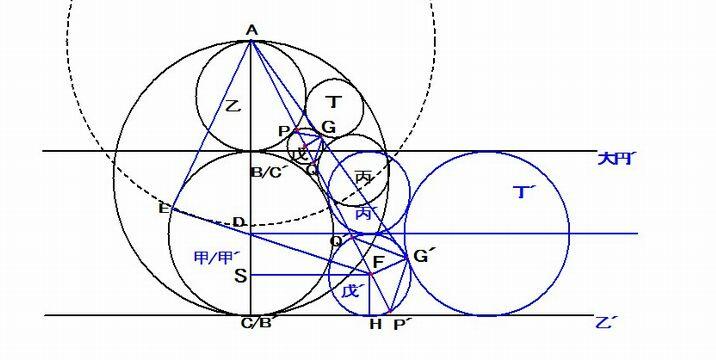
　図に示すように、点,A,B,C,D,E を定め、反転の中心を大円と乙円の接点,A,　反転係数 K^2 を点,A から甲円に

 に引いた接線 AE の長さの２乗とする反転法を使う。

  AE = K , AB = b , BC = a から　　AE^2 = AB * AC = b(b + a) = AD^2 - ED^2 = (b + (a/2))^2 - (a/2)^2=

 b^2 + 2b*(a/2)) + a^2/4 - a^2/4= b^2 + ab = b^2 +ab     K^2 = ab + b^2 = b(a +b) .・・・�@

 各点, B,C,D,E の反転を それぞれ B´,C´,D´,E´ で、各円、大円、甲、乙、丁、戊 の反転を,　それぞれ

 大円 ´、甲 ´、乙 ´、丁 ´、戊 ´　とする。　戊円 と 戊円 ´の半径を　それぞれ r , r´　とする。

戊 ´円の中心を F とし、直線 AF と戊円 との交点を P, Q とし、反転を P´,Q´ とする。

反転法の定理【定理A , 定理B】 によって     

 点 A を反転の中心、反転の半径を k とする。 反転の中心 A を通らない 戊円 の直径の両端 P, Q の反点を

それぞれ P´,Q´ とすると、P´,Q´ は定点であるから　　　　　 AP * AP´ = K^2 AQ * AQ´ = K^2

P´Q´ = CD = BC/2 = a/2

DF = CD + FH = a/2 + a/4 = 3a/4 から　�僖FS で　 SF^2 = DF^2 - DS^2 = (3a/4)^2 - (a/4)^2 = a^2/2

AF を求める。 �僊SF で    AF^2 = AS^2 + SF^2 = (3a/4 + b)^2 + a^2/2 = (17a^2 + 24ab + 16b^2)／16

           

AP´ を求める。   AP´ = AF + FP´ = √((17a^2 + 24ab + 16b^2)／16) + a/4

AQ´ を求める。 AQ´ = AP´- Q´P´ = (√((17a^2 + 24ab + 16b^2)／16) + a/4) - a/2 = 

                                                                                   

(√((17a^2 + 24ab + 16b^2)／16) + 2a/4) - a/4     ∴ AQ´ = √((17a^2 + 24ab + 16b^2)／16) + a/4

AG´^2 = AF^2 - FG´^2 = (3a/4 + b)^2 + a^2/2) - (a/4)^2 = (3a/4)^2 + 2(3a/4)b + b^2 + a^2/2) - a^2/16

9a^2/16 + 3ab/2 + b^2 + a^2/2 - a^2/16 = (9a^2 + 24ab + 16b^2 + 8a^2 - a^2)／16 = 

(16a^2 + 24ab + 16b^2)／16 = a^2 + 3ab/2 + b^2       AG´^2 = a^2 + 3ab/2 + b^2 ・・・・　�A

AP´* AQ´=  √((17a^2 + 24ab + 16b^2)／16) + a/4 * √((17a^2 + 24ab + 16b^2)／16) - a/4 =

(√((17a^2 + 24ab + 16b^2)／16))^2 - a/4(√((17a^2 + 24ab + 16b^2)／16)) + 

a/4(√((17a^2 + 24ab + 16b^2)／16)) + (a/4)(-a/4) = (17a^2 + 24ab + 16b^2)／16) - a^2/16) = 

(17a^2 + 24ab + 16b^2 - a^2)／16 = (16a^2 + 24ab + 16b^2)／16 = a^2 + 3ab/2 + b^2

　∴　AP´* AQ´= AG´^2 　 AP * AP´ = K^2 AQ * AQ´ = K^2 であるから　戊円 の直径は　　

PQ = AQ - AP = K^2/AQ´ - K^2/AP´ = K^2AP´／AP´* AQ´ - K^2AQ´／AP´* AQ´ =

K^2*((AP´- AQ´)／AP´* AQ´) = K^2*(P´Q´)／AP´* AQ´) = K^2*a／2AP´* AQ´) = K^2*a／2AG´^2

　�@ と �A より

 K^2*a／2AG´^2 = ab(a +b)／(2a^2 + 3ab + 2b^2)  ・・・・・　証明終わり