【三重県鈴鹿市山本町の鈴鹿明神社に享和元年（1801年）に掲額された算額の問題】

         

   【現代風の要訳】

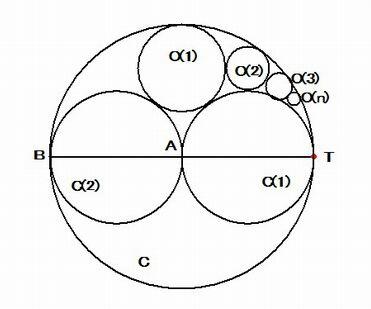
 図のように、与えられた半径 2r の円 C に内接して、その中心 A で内接する２個の円を C(1), C(2) とする。

そして、円 C に内接して、円 C(1), C(2) に外接する接する円を O(1) とする。 さらに、 

  円 C に内接して円C(1) に外接する連結して接する円 O(k) の半径を r(k) ( k=1, 2, ・・・, n ) とする　　と、つぎの等式が成り立つ。

  r(n) = 2r / ( n^2+2 )

【解答】

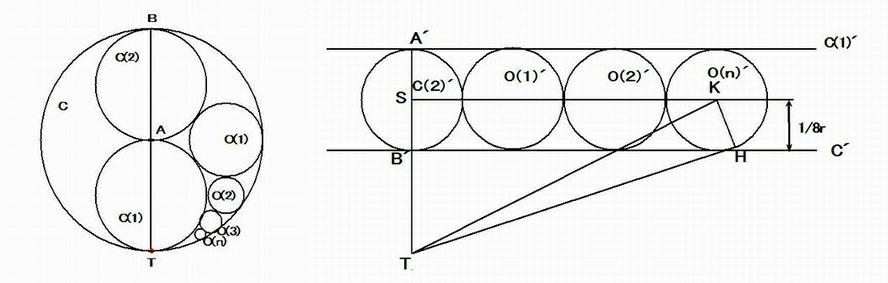
　点 T を反転の中心として、反転の円の半径を k=1 に設定する。 このとき、図の全体を反転して得られる図形を点 T を中心に負の方向に

 90° 回転すると、下の図のようになる。 （k の値を定めても、問題の本質は失われることはない。）

　この反転によって、図の細部はそれぞれ、下の図のように反転されている。 すなわち

・ 中心 T を通る２円 C, C(1) は、それぞれ、下の図の平行な２直線 C', C(1)' に反転される。

・ ２点 A, B はそれぞれ点 A', B' に反転されて、

TA = 2r, TB=4r, TA・TA' = TB・TB' = 1 から TA' = 1/2r, TB' = 1/4r

したがって A'B' = TA'−TB' = 1/2r −1/4 r= 1/4r

・ 中心 T を通る線分 AB は、中心 T を通る垂直な線分 A'B' に反転される。

・ ２円 C, C(1) に接する円 C(2) は、平行な2直線 C', C(1)' に接する円 C(2)' に反転される。

・ 円 C に内接して、円 C(1), C(2) に内接する円 O(k)' はそれぞれ連結して接する円 O(k)' (k=1,2,・・・,n) に

反転される。

　したがって、円O(k) の反転円 O(k)' の半径をそれぞれr(k)' とすると、この下の図から、連結して接する

円O(k)’ ( k=1, 2, ・・・, n ) の半径はすべて等しいことがわかる。 よって、これらの円の半径をまとめて r' とおくと  

  r' = r(k)' = A'B'/2 = 1/8r ( k=1, 2, ・・・, n ) が成り立つ。

 

   

 さらに上の図のように、円 O(n)' の中心 K 、点 T から 円 O(n)' に引いた接線の接点を H とすると、�儺SK で

∠TSK = 90° から

  KS = 2n・r' = 2n・1/8r = n/4r , TS = TB' + B'S = 1/4r + 1/8r = 3/8r 

よって 　　　 TK^2 = KS^2 + TS^2 = (n/4r)^2 + (3/8r)^2 = n^2/16r^2 + 9/64r^2 = (4n2+9) / 64r^2 

また、�儺KH で∠THK = 90° から　TK^2 = TH^2 + KH^2 , 　KH = r' = 1/8r

したがって、接線の長さ TH を L(n) と置くと

　　　　　　　 　L(n) = TH^2 = TK^2 − KH^2 = (4n^2+9) / 64r^2 − 1 /64r^2 = (4n2+8) / 64r^2 = (n^2+2) / 16r^2 

　　【注3】・・・ 【定理D】　　 等式　 r = r' k^2 / L^2　　より　

  ∴ r(n) = r(n)' / L(n)^2 = r' ・1/ L(n)^2 = 1/8r ・16r^2/ (n^2+2) = 2r / (n^2+2) （証明終わり）    

  

【注1】　反転の中心 Ｔ で接する２個の円は、点 T を通らない２本の平行な直線に反転される。

【注2】　反転の中心 Ｔ 以外の点 P で接する２個の円の反転は、点 P の反転 P' で接する２個の円となる。

【注3】　反転の中心 T を通らない半径 r の円 C が半径 ｒ' の円 C' に反転されるとき、点 T から円 C' への接線の長さを L とすると、次の等式が成り立つ。

                                                

  　　　　　　 等式　 r = r' k^2 / L^2　 が成り立つ。 　

【証明】 

                 

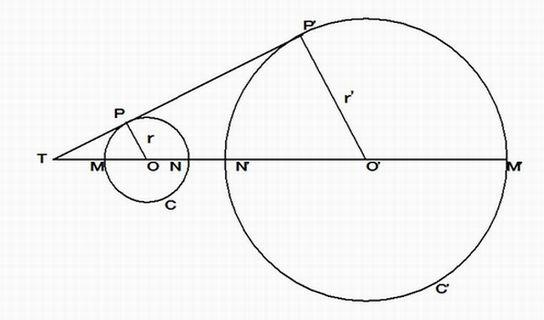
　点 T を反転の中心、反転の半径を k とする。 上の図のように、反転の中心 Ｔ を通らない円 C の中心を O の反点を

 O' 、T から円 C に引いた接線の接点 P の反点を P' とすると、点 P' は円 C' の接点となる。

このとき、反転の条件式 TM・TM' = TN・TN' = k^2 　から 

　　　　　　　　　 TM = k2/ TM' , TN = k2/ TN'  

したがって　　　

  2r = MN = TN−TM =　k2/ TN' − k2/ TM'　

  = k2 (1/T'N'−1/TM')  

  = k2(TM'−TN') / TM'・TN' ・・・・・ �@ 

 

ここで、方べきの定理によって

  TM' ・TN' = TP'^2 = L^2 

したがって、TM'−TN' = M'N' = 2r' と TP' = L と �@ から

　　　　　　　　　　2r = 2r' ・k~2/ L^2 

　　　　　　　 ∴　 　r = r' k^2 / L^2　　（証明終わり）