群馬県　倉賀野神社

【倉賀野神社 慶応３年（１８６７年） 鈴木角右衛門勝森】

｛原文｝

 今有如図三角内最多弧容甲乙丙逐円 角面八寸問得逐円径術幾何 甲円径三寸零七厘九毛有奇

 答曰 乙円径一寸二分三厘七毛五 丙円径六分六厘三毛有奇術曰 置七分五厘平方開之以除角面名極三除之得

甲円径乗極名子平方開之倍之加極及甲円径以除子得乙円径乗極名丑平方開之倍之加極及乙円径以除丑得丙円径

乗極名寅平方開之倍加極及丙円径以除寅得 

｛原文の要訳｝

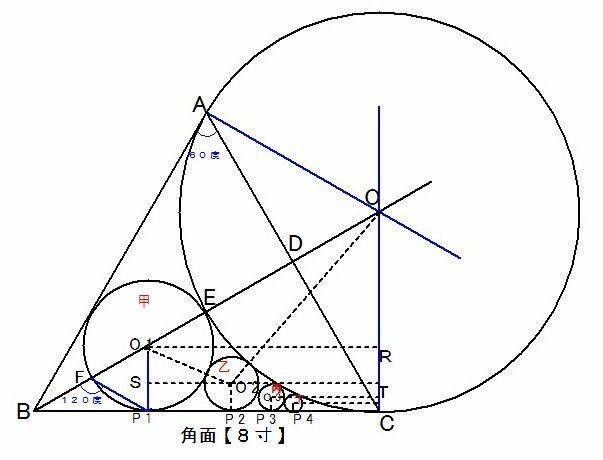
 図のように、三角（正三角形）内に最大の弧を描き、甲乙丙の逐円を容れる。

角面（正三角形の一辺）が８寸であるとき、逐円径（各円の直径）を求めよ。

正三角形ＡＢＣで、ＢＣ＝ＣＡ＝角面＝８

甲円，乙円，丙円，丁円・・・の中心をそれぞれＯ１，Ｏ２，Ｏ３，Ｏ４・・・と

する。Ｏ１，Ｏ２，Ｏ３，Ｏ４・・・から辺ＢＣへの垂線の足をＰ１，Ｐ２，Ｐ３，Ｐ４・・・とする。

ＡＤ = ＤＣ = １　/　２　×　８ = ４　

正三角形ＡＢＣの頂点Ｂから辺ＡＣへの垂線の足が、Ｄであるから

 　【三平方の定理より】

  _______________________ ___________________ __________________________________

ＢＤ＝ √BC^2　−　DC^2 = √８^2　−　４^2 = √４８ = √(2×2×2×2×3)

  ________________________

=√2＾2×√2＾2×√3 = 2×2×√3 =4√3 　　　 ＢＤ ＝ 4√3

直角三角形ＢＤＣと直角三角形ＣＯＤが相似であり、ＤＣの長さが同一から, ＯＤ の長さを求める。

ＯＤ ： ＤＣ ＝ ＤＣ ： ＢＤ　ＤＣ　＝ ４　ＢＤ　＝　4√3 により　ＯＤ　：　4　＝　4：　4√3

4√3ＯＤ ＝ １６　　ＯＤ ＝１６／4√3 ＝ ４／√3

　　　　　　　　　　　　　　　　　　　　　　　　　　 ________________________ ______________________________

ＯＣの長さを求める。 【三平方の定理より】 √ＯＤ^2　＋　ＤＣ^2 ＝　√（４／√3） ^2 ＋ ４ ^2 

  ________________________　 ___________ ___________           

＝　√１６／３　＋　１６　＝　√６４／３ ＯＣ　＝ √６４／３＝８／√3　※ ＯＥ　＝　ＯＣ　

　　　　　　　　　　　　　　　　　　　　　　 　　 　_______________________ ______________________________

ＯＢの長さを求める。 【三平方の定理より】 √ＯＣ^2　＋　ＢＣ^2 ＝　√（８／√3 ） ^2 ＋ ８ ^2

　 ________________________ ____________                         

＝　√８／√3 　＋　６４＝　√２５６／３ ＯＢ　＝１６／√３ 

                                                            

ＥＤの長さを求める。ＥＤ ＝ ＯＥ − ＯＤ ＝ ８／√3 − ４／√3 ＝ ４／√3    

ＥＤ ＝４／√３ 

　　　　　　　　　　　　　　　　　　　　　　　　　　　 　                                              

ＢＥの長さを求める。ＢＥ ＝ ＢＤ − ＥＤ＝ 4√3 − ４／√3 ＝　(√3 × 4√3)／ √3− ４／√3

１２√3− ４／√3 ＝ ８／√3　　　　ＢＥ ＝８／√３ (4.6188)

角形Ｏ１Ｐ１Ｆは、正三角形であり、三角形ＦＢＰ１は、二等辺三角形であ

ＥＯ１＝Ｏ１Ｆ＝ＢＦ＝Ｏ１Ｐ１＝ＲＣ ＝１／３ＢＥ＝１／３×８／√3＝８√3／９ (1.5396)

　極 ＝ ＯＢ ＝ ２×（８ /√３) 

★甲円径＝２ × ＥＯ１ ＝ ２ × ８√3／９ ＝ １６√3／９ ＝ ３．０７９２

乙円径を求めるには、Ｏ１Ｏ２の長さを求め、甲の半径を引けば、乙の半径が、求まります。

Ｏ１からＯＣへの垂線の足をＲとするとき、直角三角形ＲＯＯ１で

 （ＯＯ１）^2＝（ＲＯ）^2＋（ＲＯ１）^2 ＝（ＯＣ−ＲＣ）^2＋（ＲＯ１）^2

ＯＯ１＝ ＥＯ１ ＋ ＯＥ ＝ ８√3／９ ＋ ８／√3 = ３２√3／９

　　　　　　 ____________________________________ ____________________________________________________

ＲＯ1 = √ （ＯＯ１）^2 - (ＯＣ−ＲＣ）^2 ＝√ (３２√3／９)^2 - (８／√3−８√3／９）^2  ＝

  _______________________________________ ________________

√３０７２／８１ - (１６√3／９）^2 ＝√２３０４／８１＝ ４８／９ (5.333333)

ＲＯ1 の解（４８／９）が、正しいかを他の方法で検証する。

　　　　　　　　　　　　　　　　　　　　　　

ＲＯ1 =　８(角面)−ＢＰ１　ＢＯ１＝ＯＢ − ＯＯ１＝１６／√３−３２√3／９＝１６√３／９　　　　　

ＢＰ１＝√ （ＢＯ１）^2 - (Ｏ１Ｐ１）^2 ＝√（１６√３／９）^2 - (８√3／９）^2 ＝√５７６／８１

                

ＲＯ1 =８−２４／９＝ ４８／９　　∴　ＲＯ1 の解（４８／９）が、正しい値です。　

（Ｏ１Ｏ２）^２＝（ＧＯ１）^２＋（ＧＯ２）^２＝（Ｏ１Ｐ１−ＧＰ１）^２＋（ＧＯ２）^２

∴ （ＧＯ２）^２ ＝（Ｏ１Ｏ２）^２ −（Ｏ１Ｐ１−ＧＰ１）^２

（ＯＯ２）^２＝（ＨＯ）^２＋（ＨＯ２）^２ ＝（ＯＣ−ＨＣ）^２＋（ＨＯ２）^２

∴　　（ＨＯ２）^２ ＝（ＯＯ２）^２ −（ＯＣ−ＨＣ）^２

（ＯＯ１）^２＝（ＫＯ）^２＋（ＫＯ１）^２　　＝（ＯＣ−ＫＣ）^２＋（ＫＯ１）^２　

∴　　（ＫＯ１）^２ ＝（ＯＯ１）^２ −（ＯＣ−ＫＣ）^２

　　　　　　　　　　　　　　　　　　　　　　 

 Ｐ１Ｃ＝Ｐ１Ｐ２＋Ｐ２Ｃ であり Ｐ１Ｃ＝ＫＯ１　 Ｐ１Ｐ２＝ＧＯ２　 Ｐ２Ｃ＝ＨＯ２

Ｏ１Ｐ１＝ａ， Ｏ２Ｐ２＝ｂ とする。 　

ａ＋ｂ＝Ｏ１Ｐ１＋Ｏ２Ｐ２＝Ｏ１Ｏ２ ａ−ｂ＝Ｏ１Ｐ１−Ｏ２Ｐ２＝Ｏ１Ｇ

ＯＣ ＝ ＯＥ＝ ８／√3　　ＯＯ１＝ＯＥ＋Ｏ１Ｐ１(ａ) ＫＣ ＝ Ｏ１Ｐ１(ａ)  

ＯＯ２＝ＯＥ＋Ｏ２Ｐ２(ｂ) 　　　ＨＣ ＝ Ｏ２Ｐ２(ｂ)

Ｐ１Ｃ ＝ √（ＯＯ１）^2−(ＯＣ−ＫＣ）^2＝

√(Ｏ１Ｏ２)^２−（ Ｏ１Ｐ１− ＧＰ１)^２＋√(ＯＯ２)^２− (ＯＣ−ＨＣ)^２

 √（ａ＋ｂ）^2−（ａ−ｂ）^2＋√（８ /√３＋ｂ）^2−(８/√３−ｂ）^2  

√ａ^2＋２ａｂ＋ｂ^2−（ａ^2−２ａｂ＋ｂ^2）＋(８ /√３)^2＋２(８ /√３)ｂ＋ｂ^2−

((８ /√３)^2−２(８ /√３)ｂ＋ｂ^2)

Ｐ１Ｃ ＝√（８ /√３＋ａ）^2−(８/√３−ａ）^2＝√４×(８ /√３)×ａ＝

√４×ａ×ｂ＋√４×（８ /√３)×ｂ）

両辺を平方する

(√４×(（８ /√３)×ａ)^2＝(√４×ａ×ｂ＋√４×（８ /√３)×ｂ)^2

４×（８ /√３)×ａ =４×ａ×ｂ＋４×（８ /√３)×ｂ

４×（８ /√３)×ａ =４×ａ×ｂ ＋４×（８ /√３)×ｂ＋２×√(４×ａ×ｂ)=

√４×（８ /√３)×ｂ

(２×（８ /√３))×２ａ =２ａ×２ｂ＋(２×（８/√３))×２ｂ＋２×√２ａ=

√(２×（８ /√３))×２ｂ=２ａ＋ (２×（８ √３)＋ √２×（８/√３)×２ｂ

２ｂ =((２×（８ /√３))×２ａ)/(２ａ＋(２×√２ａ) × (２×（８ /√３))

∴　乙円径（乙円の直径）２ｂは 　　　甲２ａ 　極＝２×（８ /√３) 　子＝ 甲× 極

乙円径＝ 甲× 極/ (甲＋ 極＋２（√甲× 極)＝子/ (甲＋ 極＋２√子)

 甲円径＝１/３× 極 極 ≒３．０７９２０１ 子 甲 極 ≒２８．４４４４３９

乙円径＝子/ (甲＋ 極＋２√子) ≒１．２３７６０４