姤堫壸恄幮乮孮攏導懢揷巗乯
恾偺傛偆偵丄惓巐柺懱偺撪偵戝彫偦傟偧傟係偮偺媴偑愙偡傞傛偆偵偁傞丅戝偺係媴偼惓巐柺懱偺嶰柺偵
愙偟丄彫偺侾媴偼惓巐柺懱偺嶰柺偵愙偟丄彫偺俁媴偼丄惓巐柺懱偺擇柺偲戝彫媴偺昞柺偵偣偭偟偰偄傞丅
偙偙偱戝媴偺捈宎傪俀俈丏俁悺偲偡傞偲丄彫媴偺捈宎偼丄偄偔傜偐丅
堦椗(懡柺懱偺偲側傝偁偭偨擇偮偺柺偑岎傢偭偰側偡捈慄)偺挿偝偑倎偱偁傞惓巐柺懱偼丄偑倎偱偁傞
惓嶰妏宍係柺偱峔惉偝傟偰偄傞丅壓偺搳塭恾偵倎偺幚挿偑昞傟偰偄傞偺偼丄暯柺恾偺掙曈偺惓嶰妏宍偺
俛乫俠乫亖俠乫俢乫亖俢乫俛乫偺奺曈偲棫柺恾偺椗俙俛偑幚挿偱偁傞丅傑偨懁柺偺惓嶰妏宍偺崅偝偺幚挿偑昞傟
偰偄傞偺偼暯柺恾偺俛乫俤乫偲棫懱恾偺俙俤偲偱偁傝丄偦偺幚挿偼丄岞幃偵傛傝丂倛亖倎亊(併俁乛俀)丂偱偁傞丅
(惓嶰妏宍偺堦曈偺崅偝乯亊併俁亐俀丂丂偱偡丅
丂丂丂丂丂丂丂丂丂丂
仮俙俛G 偍傛傃仮俙俠G 偼捈妏嶰妏宍偱偁傞偐傜丆 俙俛 = 俙俠 傛傝 仮 俙俛G佭俙俠G
{佭 (崌摨婰崋) }丂丂丂亪G俛= G俠 俙俛 = 俙俠 = 俙俢 偱偁傞偙偲傛傝丆摨條偵仮俙俢G 偵偮偄偰傕峫偊傞偲丆
G俛 = G俠 = G俢 埲忋傛傝丆揰G 偼嶰妏宍俛俠俢 偺奜怱偱偁傞丏 偙偙偱丆惓嶰妏宍偺奜怱偲廳怱偼堦抳
偡傞偐傜丆捈慄俛G 偲曈俠C 偲偺岎揰傪 俤 偲偡傞偲丆 俛G:G俤 = 2 :1 偱偁傞丏
亂嶰妏宍偺崌摨忦審丂乮懳墳偡傞曈傗妏傪乽慻乿偱昞偡乯亃
侾乯俁慻偺曈偑偦傟偧傟摍偟偄丅
俀乯俀慻偺曈偲偦偺娫偺妏偑偦傟偧傟摍偟偄丅
俁乯侾慻偺曈偲偦偺椉抂偺妏偑偦傟偧傟摍偟偄丅
亂嶰妏宍偺憡帡忦審亃
侾乯俁慻偺曈偺斾偑偡傋偰摍偟偄丅
俀乯俀慻偺曈偺斾偲偦偺娫偺妏偑偦傟偧傟摍偟偄丅
俁乯俀慻偺妏偑偦傟偧傟摍偟偄丅
惓巐柺懱傪峔惉偡傞惓嶰妏宍偺廳怱偼掙柺俛俠俢偱偼丄揰俧偱偁傝丄傑偨懁柺俙俠俢偱偼揰俥偱偁傞丅
偟偨偑偭偰
俙俥亖俛俧亖(俀乛俁)倛亖(併俁乛俁)倎丂丂丂俥俤亖俧俤亖(侾乛俁)倛亖(併俁乛俇)倎
惓巐柺懱偺崅偝偱偁傞俙俧丱俀亖俙俤丱俀亅俧俤丱俀亖乮(併俁乛俀)倎乯丱俀亅(乮併俁乛俇)倎乯丱俀亖
(乮俁乛係)倎)丱俀亅乮(併俁乛俇)倎乯丱俀亖(乮俁乛係)倎乯丱俀亅(乮俁乛俁俇)倎乯丱俀亖
乮俋乛侾俀亅侾乛侾俀乯丱俀丂丂丂丂丂丂俙俧亖(併俇乛俁)倎丒丒丒嘆丂
傑偨惓巐柺懱偺崅偝偵偁偨傞慄暘俙俧偲俛俥偲偺岎揰俷偼丄惓巐柺懱偺廳怱偱偁傞丅
惓巐柺懱偵撪愙偡傞媴偼偦偺俀偮偺廳怱傪嫟桳偡傞丅
惓巐柺懱偺奺椗傪倎丄偦偺撪愙媴偺捈宎傪俲偲偡傞捈妏嶰妏宍俛俤俥偲BOG偲偼丄憡帡偱偁傞偐傜
俛俤丗俛俷亖俤俥丗俷俧亖俛俤亊俷俧亖乮俛俥亅俷俥乯亊俤俥亖(併俁乛俀)倎亊俲乛俀亖
乮併俇乛俁)倎亅俲乛俀乯亊(併俁乛俇)倎丂丂俲乛俀亖(併俇乛(俁亊俁))倎亅(俲乛俀亊侾乛俁)亖俋俲亖
(俀併俇)倎亅俁俲 俲亖(併俇乛俇)倎
偟偨偑偭偰丄撪愙媴偺捈宎偼丄偙偺惓巐柺懱偺崅偝俙俧偺侾乛俀偱偁傝丄俙俫亖俫俧偱
傑偨敿宎偼丄(併俇乛侾俀)倎偱偁傞丅
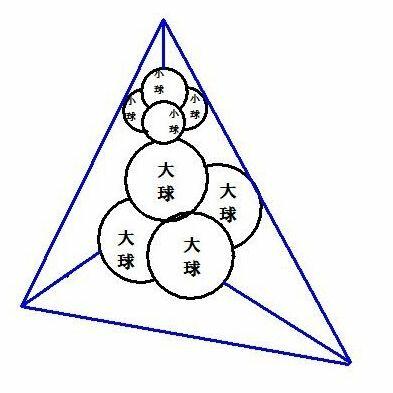
捈宎偑俴偱偁傞係摍媴偑恾偺傛偆偵愙偟偰偄傞丅係媴偺拞怱傪寢傫偱偱偒傞棫懱
俴丆俴2丄俴3丄俴4偼丄堦椗偺挿偝俴偱偁傞惓巐柺懱偱偁傝丄偦偺崅偝偱偁傞 俴俹 偼丄
嘆傪揔梡偟偰丄俴俹 亖丂(併俇乛俁)俴丒丒丒嘇丂丂偟偨偑偭偰係媴慡懱偺崅偝
俫俧亖俫俴亄俴俹亄俹俧亖俴乛俀亄(併俇乛俁)俴亄俴乛俀亖(併俇乛俁)俴亄俴丒丒丒嘊
戝媴傪俵乮倣乯丄彫媴傪俴乮倶乯丆俴2乮倶乯俴3乮倶乯俴4乮倶乯丂偲偡傞丅
俙俵亖俙俴亄俴俹亄俹俵 俙俴偼乮俀乯傛傝彫媴宎偺俁乛俀攞偱偁傝摨條偵俙俵偼
戝媴宎偺俁乛俀攞偱偁傞丅 俴俹偼乮俁乯偺嘇幃偱偁傞丅丂丂丂
____________________
俴亖倣丂俲亖倶丂偲偡傞丅 俹俵亖併俴俵^2亅 俴俹^2亖併乮乮倣亄倶乯^2乛俀乯亅乮併俁乛俁乯^2
亖併乮乮倣亄倶乯^2乛俀乯亅乮倶^2乛俁乯亖併乮乮倣^2亄俀倣倶^2亄倶^2乯乛係乯亅乮倶^2乛俁乯
俁倣乛俀亖俁乛俀倶亄併乮俀倶乛俁乯亄併乮乮倣^2亄俀倣倶^2亄倶^2乯乛係乯亅乮倶^2乛俁乯
併乮乮倣^2亄俀倣倶^2亄倶^2乯乛係乯亅乮倶^2乛俁乯亖俁倣乛俀亅俁倶乛俀亅併俇倶乛俁
乮倣丱俀亄俀倣倶亄倶丱俀乯乛係亅倶丱俀乛俁亖俋倣丱俀乛係亄俋倶丱俀乛係亄俇倶丱俀乛俋
俁倣^2亄俇倣倶亄俁倶^2亅係倶^2亖俀俈倶丱俀亄俉倶丱俀亄俀俈倣丱俀亅俆係倣倶
亅侾俀併俇倣倶亄侾俀併俇倶丱俀
俁俇倶丱俀亄侾俀併俇倶丱俀亅俇侽倣亅侾俀併俇倣倶亄俀係倣丱俀亖侽
乮俁亄併俇乯倶丱俀亅乮俆亄併俇乯倣倶亄俀倣丱俀亖侽
倶亖乮俆亄併俇亇併乮俆亄併俇乯丱俀亅俉乮俁亄併俇乯乯倣乛俀乮俁亄併俇乯
亖乮俆亄併俇亇併俀俆亄侾侽併俇亄俇亅俀係亅俉併俇乯倣乛乮俇亄俀併俇乯
亖乮俆亄併俇亇併俈亄俀併俇乯倣乛乮俇亄俀併俇乯亖乮俆亄併俇亄侾亄併俇乯倣乛乮俇亄俀併俇乯
亖乮俇亄俀併俇乯倣乛俇亄俀併俇亖倣丂丂乮倶亖倣偲側傝 亇 偺 亄 偼丄晄揔乯
劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒
倶亖乮俆亄併俇亅侾亅併俇乯倣乛俀乮俁亄併俇乯亖係倣乛俀乮俁亄併俇乯亖俀倣乛乮俁亄併俇乯亖
俀亊俀俈丏俁乛乮俁亄併俇乯亖俆係丏俇乛乮俁亄併俇乯亖侾侽丏侽侾俋俀俉俇