�V���^�C�i�[�̉~�̒藝
�@
�����̉~���V���^�C�i�[�̉~���Ȃ��Ă���Ƃ��C �����������Ă���~�̉~�̔��a�̋t���̘a�͈��ł���D
�� �ؖ� ��
�~O_1���~O_2���܂�Œ�܂�C���a��R��r�Ƃ���D �����ĉ~ C_1, C_2, �E�E�E C_2n���~���Ȃ��Ă���D
�_O�𒆐S�Ƃ��锼�a���̔��]�� �~O_1�CO_2�����S�~O_1'�CO_2'�ɂȂ肻�̔��a��R', r'�Ƃ���D
C_i', i=1, 2,�E�E�E , 2n�̔��a�͂��ׂē������̂ł����r_0'�Ƃ���D
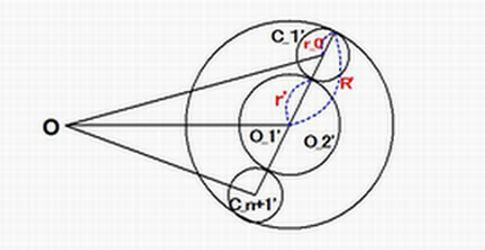
R'-r'=2r_0'
�ł���D �����āC���̂Ƃ�C_1'��C_n+'�̒��S C_1'�� C_n+1' �����O_1'�CO_2'�̒��S O_1'�͓���������ɂ���D
�藝�R ���
r_1/r_0'.= ��^2/(OC_1'^2-r_0'.^2) �C.r_n+1/r_0' = ��^2�^(OC_n+1'^2-r_0'^2)
����������藝��p�����
1/r_1+1/r_n+1= (1/r_0'��^2)+ OC_n+1'^2 - 2r_0'^2) = (2/r_0'��^2)(OO_1'^2+ O_1'C_1'^2 - r_0'^2)
= (2/r_0'��^2)(OO_1'^2+ (r' + r_0)^2 - r_0'^2) = (2/r_0'��^2)(OO_1'^2+ r'^2 + 2r'r_0')
= (4/ (R'-r')��^2)(OO_1'^2+ r'^2 + r^(R'-r')) = (4/ (R'-r')��^2)(OO_1'^2+ r'R')
����C�藝�R �� R, r, R', r�ɗp����
1/r - 1/R = (OO_1'^2 - r'^2)/r'��^2 - (OO_1'^2 - R'^2)/R'��^2 = (R'-r')(OO_1'^2+ r'R')/r'R'��^2
�� 1/r - 1/R = 1/r_1+1/r_n+1= 4r'R'( 1/r - 1/R)�^(R'-r')^2�E�E�E�i���ƂȂ�j
�@ �藝�Q���O_1, O_2�̒��S�Ԃ̋�����d�Ƃ���@
d^2 = (R�|��')^2 �|4R��������^2(��/��)�@�@�@�@((R�|��')^2 - d^2) �^4R�� = ������^2(��/��)
((R-r)^2 - d^2)�^rR = (R'-r')^2/r'R' ���ꂩ��
1/r_1+1/r_n+1= 4(R-r)�^((R-r)^2 - d^2)�@�@�ƂȂ�B�@�@�@�@�@�@n = 4 �̂Ƃ���
�@�@ ((R-r)^2 - d^2)�^rR = 4 1/�� 1 + 1/�� 3 = 1/�� 2 + 1/�� 4 = 1/r - 1/R ����������
�@ �yn = 6 �̂Ƃ��́z
�@�@�@�@�@ 1/�� 1 + 1/�� 4 = 1/�� 2 + 1/�� 5 = 1/�� 3 + 1/�� 6 ����������
���藝 �P��
�݂��Ɍ����Ȃ���~C_1,C_2������D��~�̏œ_F�𒆐S�Ƃ��锽�]�ł�����~��
���S�~ �ɂ���D
���ؖ��� ��~��
�����Ɠ�~C, C'�̒��S�����Ԓ���J�Ƃ̌�_��K�𒆐S�Ƃ��C ��̏œ_��ʂ�~S�͓�~C_1, C_2�ƒ������Ă���D
�~S��F��ʂ�̂ŁC F���S�Ƃ��锽�]�Œ���m�ɂȂ�D ����C��~C_1,C_2�͂��ꂼ��Ăщ~ C_1',C_2�ɂ��邪�C �����̉~��m�ƒ������Ă���̂ŁC
���̒��S��m��ɂ���D
����C��~C_1, C_2�̒��S�Ɣ��]�̒��S�͓�~C_1, C_2�̏œ_�����Ԓ���J��ɂ���̂ŁC �~ C_1',C_2'�̒��S��J��ɂ���D
�]���ĉ~ C_1',C_2'�̒��S��m�ォ��J��ɂ���̂ŁC ���̌�_�Ɉ�v����D�܂�~ C_1',C_2'�̒��S�͈�v����D
�{�藝�́C����̉~�������Ɋ܂܂��ꍇ�����l�ł���D
���œ_�̐�����
�~�̏W���������Ă��̂ǂ̓�̍������Ƃ��Ă����ׂĈ�v����Ƃ��C ���̉~�̏W���������ɂ���Ē�܂�~���Ƃ����D
��~C, C'�����L�_�������Ȃ��Ƃ���D ���̓�~�̍����Ɠ�~C, C'�̒��S�����Ԓ���J�Ƃ̌�_��K�Ƃ���D
K���� C, C'�ւ̐ڐ��̒��� KT=KT'�ɑ��� J��̓_�� KT=KF �ƂȂ�_�͓�_����D
����� F,F'�� 2�~C, C'�̏œ_�Ƃ����D
�@���藝 �Q��
�����Ȃ���~�n_1�Ƃn_2�����蔼�a��R��r�ŁC �n_2�͂n_1�̓����ɂ���D O_1�ɓ��ڂ�O_2��
�O�ڂ��C�݂��ɊO�ڂ���n�̉~ C_1�E�E�E, C_n ���Ȃ�V���^�C�i�[�̉~���\���ł����Ƃ���.
(1) �ŏ��̉~C_1���ǂ��ɂƂ��Ă����ɊO�ڂ����ĉ~��`���Ă䂭��C_n��C_1�ɊO�ڂ���D
(2) ��~O_1��O_2�̒��S�Ԃ̋�����d�Ƃ���B�@�Q�̉~�̊Ԃɋl�߂��~�̌�n �̊Ԃɂ͎��̃V���^�C�i�[�̓����ƌĂ��W�������藧���Ă���B
d^2 = (R�|��')^2 �|4R��������^2(��/��)
�� �ؖ� ��
1) �}�̂悤��O_1��O_2�̏œ_F���Ƃ�CF�𒆐S�Ƃ��锽�]�������Ȃ��D�藝�P�ɂ���āCI�̏�Ԃ���II�̏�Ԃɔ��]�����
���S�~�̊Ԃ�n�̉~���݂��ɊO�ڂ��Ă͂��܂��Ƃ��́C ���a���������ŁCn�̉~����ł���ǂ�����͂��߂Ă�n�ʼn~���ł���D
�ŏ�O_1��O_2�̊Ԃ�C_1�������D ���̔��]C_1'����͂��߂ē��S�~�̕���n�̉~������D ����]�̋t�������Ȃ����Ƃɖ߂���C_1����͂��܂�~���ł��Ă���D
2) O_1��O_2�]�����~�̔��a��R', r'�Ƃ���D ���̏ꍇC_1'���̔��a�� (R'-r')/2�ŁC C_1'��C_2'�̒��S C_1'��C_2'�� O_1'�̒��S O_1'�ƂȂ��p��
2��/��( �ڍׁE�E�E�ʓx�@�i���W�A���j�@�Q�Ɓj�DO_1'�̒��S O_1'�CC_1'��C_2'�̐ړ_A�C C_1'�̒��S C_1'����钼�p�O�p�`���
�~�̐�n ���A�����̔��a�͂��ׂē��������A��������Ƃ���B
sin��/n = x/(R - x) ������ (R - x)sin��/n = x(R - x)/(R - x) (R - x)sin��/n = x
x = (Rsin��/n) - xsin��/n 2x = R - r ���@ 2R - 2r = 2((Rsin��/n) - (R - r)sin��/2n)
2R - 2r = 2((2Rsin��/2n) - Rsin��/2n + rsin��/2n) = 2((Rsin�� + rsin��)/2n)
2R - 2r = (Rsin�� + rsin��)/n -2r = (Rsin�� + rsin��)/n - 2R 2r = 2R - (Rsin�� + rsin��)/n
r = R - (Rsin�� + rsin��)/2n
���̎��ɂ��A��~�̔��aR �ƂQ�̉~�ɓ��ڂ���~�̐�n ���w�肷��A���~�Ɠ��ڂ���~�������I�Ɍ��肳���B
�@���� { d^2 = (R�|��')^2 �|4R��������^2(��/��) } �����̂悤�ɕό`����B�@
�@�@((R�|��')^2 - d^2) �^4R�� = ������^2(��/��)
�� �ؖ� ��
���ӂ͔��]�ŕs�ςł��邱�Ƃ��܂������B���̌�A�Q�~�S�~�ɔ��]�ňڂ����ꍇ�ł��̒l���v�Z���A
���ꂪ�E�ӂɓ��������Ƃ������B
��~��x ���Ƃ̌�_�����W�̏�����������A(a) , B(b) ,���~��x ���Ƃ̌�_�����W�̏�����������
C(c ), D(d) �Ƃ���B
R = (b - a)/2, r = (d - c)/2, d = (a + b)/2 - (c + d)/2
�䂦�� R - r + d = (b - a)/2 - (d - c)/2 + (a + b)/2 - (c + d)/2 = b - d
R -.r -.d = (b - a)/2 - (d - c)/2 - (a + b)/2 + (c + d)/2 = c -.a
����āA���� = ((R - r )^2 - d^2)�^4Rr = (R - r + d )(R -.r -.d )�^4Rr =
(b. - d )(c - .a)�^(4((b - .a)(d. - c))�^4)�@= (b - d )(c - a)�^(b - a)(d - c)�E�E�E�B
�������Ƃ]�ňڂ�����ł��l����B
���]��A ,B ,C ,D ��A0(a0), B0(b0),C0(c0), D0(d0) �ɂȂ����Ƃ��A�召�Q�~�̔��a��R0 , r0 �ƂȂ����Ƃ���ƁA���
�v�Z�Ɠ��l�ɂ���((R0 - r0)^2 - d0^2)�^4R0r0 = (b0 - d 0)(c0 - a0)�^(b0 - a0)(d 0 - c0)�ł��邪�A���]�̐���
���@a0 = 1/a, b0 = 1/b, c0 = 1/c,d 0 = 1/d �Ȃ̂ő������
((R0 - r0)^2 - d0^2) �^4R0r0 = (b0 - d 0)(c0 - a0)�^(b0 - a0)(d 0 - c0) = (1/b- 1/d )(1/c - 1/a)�^
(1/b - 1/a)(1/d - 1/c ) = (b -.d )(c -.a)�^(b - a)(d - c)�E�E�E�C
�B�C���A���ӂ̒l�͔��]�ŕs�ςł���B
���ɂ��̕s�ϒl�����߂�B�K���Ȕ��]�ő召�Q�~�͓��S�~�Ɉڂ���邩��A���̏ł� d = 0 �ł���B
�@�A���R - r = 2x = 2 Rsin��/n�^1+sin��/n, r = R(1- sin��/n)�^1+sin��/n
����āA����= ((R - r )^2 - .d^ 2)�^4Rr = (((2Rsin��/n)�^(1+sin��/n )^2) - 0)�^(4RR(1- sin��/n)�^
(1+sin��/n)) = sin^2��/n�^1-.sin2��/n = sin2��/n�^cos2��/n = tan^2��/n ����ďؖ����ꂽ�B
(�⑫�j�E�E�E ���p�̌��� ����
cos^2(��/2) = (1 + cos ��)/2. sin^2(��/2) = (1 - cos ��)/2 �� �� = 2�� (�Ɓ@�͊p�x)
�@������^2(��/2) = sin^2(��/2)/cos^2(��/2) = 2sin^2(��/2)/(2cos^2(��/2)) = (1 - cos ��)/(1 + cos ��).
�@������^2(��/��) = sin^2(��/��)/cos2^(��/��) = 2sin^2(��/��)/(2cos^2(��/��)) = (1 - cos ��)/(1 + cos ��).
�@���藝 �R��
O��ʂ�Ȃ����ar�̉~C�C���SC������D ���̔��]�̉~��C'�C���a��r'�Œ��S��C'�Ƃ���D
���̂Ƃ� �@ r/r' = ��^2/(OC'^2 - r' ^2)�@�@�����藧�B
�� �ؖ� ��
�@�@�@�@�@�@
�@ O����C�CC'�܂ł̐ڐ��̒��������ꂼ��
_______________�@�@�Q�Q�Q�Q__�Q
��OC^2 - r^2, ��OC'^2 - r'^2 �ł���D���ړ_�����]�̊W�Ȃ̂Őς͂�^2�ł���D �����
________________ _________________
r/r' = ��OC^2 - r^2 �^��OC'^2 - r'^2 = ��^2/(OC'^2 - r'^2)
�@�@�@�@�@�@�����]�ɂ����W�ϊ��� f (x , y ) = ( x/(x2+y2) , y/(x2+y2) ) �ł���B��
�� ���]�ɂ��ؖ� ��
�܂��A��ʂ̈ʒu�ɂ���Q�̑�~�Ə��~�S�~�ֈڂ����߂̔��]�̒��S�����݂��邱�Ƃ��������ƂŁA�Q�̉~�����S�~�Ɉڂ����悤�Ȕ��]�����݂��邱�Ƃ������B
��~�Ə��~�͉��}�̂悤�Ȉʒu�ɂ���Ƃ��Ĉ�ʐ�������Ȃ��B�i���~�͑�~�̒��Ɋ܂܂��Ƃ���j
x ���Ƒ�~�Ƃ̌�_������A,D �Ƃ��A���~�Ƃ̌�_������B,C �Ƃ���B
OA = x , AB = b , AC = c , AD = d �Ƃ����B ���̂Ƃ� x > 0 , 0 < b <c < d �ł���B
���_�𒆐S�Ƃ��锽�]�ɂ��A ,B ,C , D �̕ϊ���̓_�� A0, B0,C0, D0 �Ƃ����
A0(1/x), B0( 1/x+b ),C0( 1/x+c ),D0( 1/x+d ) �ƂȂ�B ����Ĕ��]�ɂ���ĂQ�̉~�����S�~�Ɉڂ����Ƃ����
1/(x+b) -1/x = 1/(x+d) - 1/(x+c) ���Ȃ킿 1/x + 1/(x+d ) = 1/(x+b) + 1/(x+c) �ł���B
���������A(b+c-d )x^2+2bcx+bcd = 0 �ƂȂ�B
���̔��ʎ��� D/4 = a^2b^2+(b+c-d)�Ebcd = bc(d-c)(d-b) > 0 �ƂȂ�B
���������Ĕ��]�̒��S�͂Q����B
�ȏ�̂��Ƃ���Q�̑�~�Ə��~��K���Ȕ��]�ɂ�蓯�S�~�Ɉڂ����Ƃ͉\�ł���B
�ȏ�̂��Ƃ𗘗p���A�ؖ�����B
��̂悤�Ȉ�ʂ̈ʒu�ɂ����~�Ə��~���l����B�i�������A���~�͑�~�̒��Ɋ܂܂��Ƃ���j
���̂Ƃ��Q�̉~�̊Ԃɓ��ڂ���~��C�ӂ̈ʒu���玟�X�ƕ`���Ă����A�Ō�̉~���҂�����Ƃ͂܂����Ƃ���B�E�E�E�@
���̂Ƃ��K���Ȕ��]���s���Α�~�Ə��~�͓��S�~�Ɉڂ���A�Q�̉~�̊Ԃɂ͓������a�̉~���҂�����Ɠ��ڂ��Ă���B

