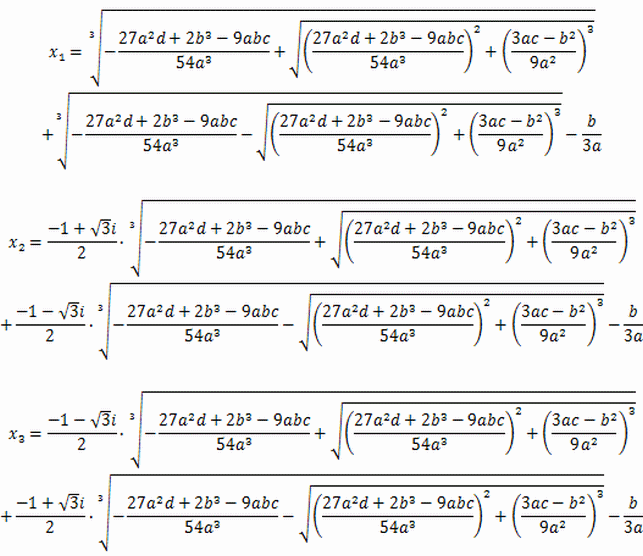渋谷 金王八幡宮の算額
伊佐爾波神社 【 嘉永7年(1850)正月 山崎昌竜門人吉田茂兵衛昌寿 奉納
{原文} (カ・・個)
今有如圓交畫大員一个中員二个面其 容小員六个大員径五百九十三寸
問中員径幾何
答曰 中員径四百六十三寸有奇
術曰 置一十七 平方開之内 一 如乗大径四之得中径合問
{原文の要訳}
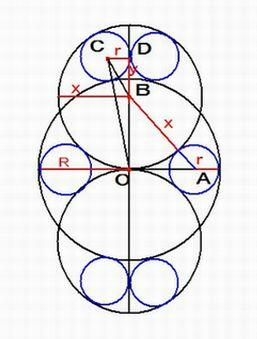
図のように、交差した大円1個と中円2個があって、その隙間に納まるように小円6個を内接させる。大円の直径が
593寸であるとき、中円の直径を求めよ。
{計算方法}
大円O(半径R), 小円 A(半径 r), 小円 C(半径 r), 中円 B(半径 x)とする。
二つの小円の接点を Dとする。 BD = y とする。
直角三角形OABにおいて OA^2 + OB^2 = AB^2 から (R - r)^2 + x^2 = (x + r)^2 ・・・①
直角三角形BCDにおいて BD^2 + CD^2 = BC^2 から y^2 + r^2 = (x - r)^2 ・・・②
直角三角形BCDにおいて CD^2 + OD^2 = OC^2 から r^2 + (x + y)^2 = (R + r)^2 ・・・③
①から R^2 - 2Rr + r^2 + x^2 = x^2 + 2rx + r^2 2rx = R^2 - 2Rr + r^2 + x^2 - x^2 - r^2
2rx = R^2 - 2Rr 2rx + 2Rr = R^2 2r(x+ R) = R^2 2r = R^2/(x+ R) ・・・④
②と④から y^2 + r^2 = x^2 - 2rx + r^2 y^2 = x^2 - 2rx ・・・⑤ y^2 = x^2 - (R^2x/(x+ R)) ・・・⑥
③と⑤から r^2 + x^2 + 2xy + x^2 - 2rx = R^2 + 2Rr + r^2
2x^2 + 2xy = R^2 + 2Rr 2x^2 + 2xy = R^2 + 2Rr + 2rx = R^2 + 2r(x + R)
④を代する。 2x^2 + 2xy = R^2 + (R^2/(x+ R)) (x + R) xy = R^2 - x^2 x^2y^2 = (R^2 - x^2)^2
⑥を代入して、xについて整理すると x^2(x^2 - (R^2x/(x+ R))) = R^4 - 2R^2x^2 + x^4
x^4 - (R^2x^3/(x+ R)) = R^4 - 2R^2x^2 + x^4 - (R^2x^3/(x+ R)) = R^4 - 2R^2x^2
(R^2x^3/(x+ R)) = 2R^2x^2 - R^4 (x+ R)(R^2x^3/(x+ R)) = (x+ R)(2R^2x^2 - R^4)
R^2x^3 = (2R^2x^2 - R^4)(x+ R) x^3 = ((2R^2x^2 - R^4)/R^2)(x+ R)
x^3 = (2x^2 - R^2)(x+ R) 2x^3+ 2Rx^2 - R^2x - R^3 = x^3 2x^3 - x^3 + 2Rx^2 - R^2x - R^3 = 0
x^3 + 2Rx^2 - R^2x - R^3 = 0 大円の直径が593寸より R = 593/2 3次方程式を解く
x^3 + 2Rx^2 - R^2x - R^3 = x^3 + 593x^2 - (593/2)^2x - (593/2)^3 =
x^3 + 593x^2 - 87912.25x - 26065982.125 = 0
x1 = -666.229 x2 = -164.545 x3 = 237.7745 (誤差=-14.0628149807)
x = 475.5 /2 寸 余り有
中円の直径 463 寸 余り有 (x = 231.5)
☆☆3次方程式☆☆
★★現代の三次方程式の解の公式は長すぎる★★
3次方程式の解の公式は「カルダノの公式」、4次方程式の解の公式は「フェラーリの公式」と呼ばれています。
そして、実は5次方程式の解の公式は存在しないことが証明されているのです...
3次方程式 x^3 + ax^2 + bx - c = 0 の解は次の3つだと言えます。
【カルダノの公式】
詳細は、 3次方程式の解の公式 ・・・参照
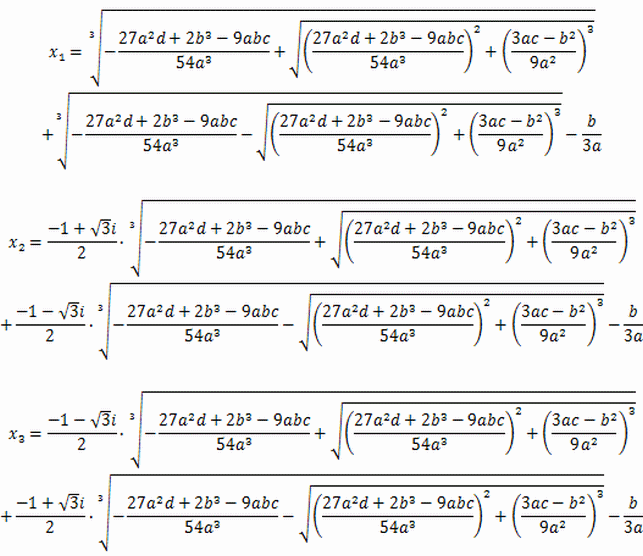
★★江戸時代の和算で三次方程式を解きます★★
x^3 + 593x^2 - 87912.25x - 26065982.125 = 0 ・・・を解きます
★ 「商」の位が、3桁のときの方程式の展開式★
X^3 = (a+b+c)^3 ★aは百の位、bは十の位、cは一の位★
(a+b+c)^3 = a^3+b^3+c^3+3ab(a+b)+3bc(b+c)+3ca(c+a)+6abc
X^2=(a+b+c)^2 ★aは百の位、bは十の位、cは一の位★
(a+b+c)^2 = a^2+b^2+c^2+2ab+2bc+2ca
x^3 + 593x^2 - 87912.25x - 26065982.125 = 0 の展開式 X^3+12X^2-2234X+32867=0
25785066.75(237) 26148048.5(238)
(8000000) (4167000) (1145053)
a^3 + b^3 + c^3 + 3ab(a+b) + 3bc(b+c) + 3ca(c+a) + 6abc (13312053)
(23720000) (7649700) (1938517)
593(a^2+b^2+c^2+2ab+2bc+2ca) (33308217)
(-20835203.25)
- 87912.25(a+b+c) - 26065982.125 =0
★★a^3 + b^3 + c^3 + 3ab(a+b) + 3bc(b+c) + 3ca(c+a) + 6abc +
593(a^2+b^2+c^2+2ab+2bc+2ca)- 87912.25(a+b+c) - 26065982.125 = 0 ★★
| 千万 |
百万 |
十万 |
万 |
千 |
百 |
十 |
一 |
分 |
厘 |
毛 |
糸 |
|
| ① |
|
|
|
|
|
|
|
商 |
|
|
|
|
 |
 |
 |
 |
 |

|
 |
 |
実 |
 |
 |
 |
|
|
|
|
 |
 |
 |
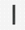 |
 |
法 |
 |
 |
|
|
|
|
|
|
|
 |
 |
 |
廉 |
|
|
|
|
|
|
|
|
|
|
|
 |
隅 |
|
|
|
|
① 商=答,実=定数項,法= x の係数,廉= x2 の係数,隅= x3の係数... ということです
x^3 + 593x^2 - 87912.25x - 26065982.125 = 0
(隅) (廉) (法) (実)
隅+廉ー法ー実 = ー実+(-法)+隅+廉=0
10 20 -5 -25 -25 -5 10 20
| 千万 |
百万 |
十万 |
万 |
千 |
百 |
十 |
一 |
分 |
厘 |
毛 |
糸 |
|
| ② |
|
|
|
|
 |
|
|
商 |
|
|
|
|
 |
 |
 |
 |
 |

|
 |
 |
実 |
 |
 |
 |
|
|
|
|
 |
 |
 |
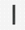 |
 |
法 |
 |
 |
|
|
|
|
|
|
|
 |
 |
 |
廉 |
|
|
|
|
|
|
|
|
|
|
|
 |
隅 |
|
|
|
|
1x^3 + 593x^2 - 87912.25x - 26065982.125 = 0
② 「商」の百の位を求める
-87912.25x{ -87912.25(a+b+c)}の a=300だと -87912.25 × 300 = -26373675 で、
-26065982.125を、超える為、「商」の百の位を 2 とします。
| 千万 |
百万 |
十万 |
万 |
千 |
百 |
十 |
一 |
分 |
厘 |
毛 |
糸 |
|
| ③④ |
|
|
|
|
 |
|
|
商 |
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
実 |
 |
 |
 |
|
 |
 |

|
 |
 |
 |

|

|
法 |
|
|
|
|
|
|
|
|
|
 |
 |
 |
廉 |
|
|
|
|
|
|
|
|
|
|
|
 |
隅 |
|
|
|
|
-87912.25x{87912.25(a+b+c)}より・・・- 87912.25a を求める
③ 「商」の200と「法」を掛けて・・200×-87912.25=-17582450 を「法」とする。
-43648432.125
④ 「法」の-17582450 を[実」に加える。 -26065982.125 +(-17582450) = -43648432.125
★「実」を -43648432.125 に置き換える。
| 千万 |
百万 |
十万 |
万 |
千 |
百 |
十 |
一 |
分 |
厘 |
毛 |
糸 |
|
| ⑤⑥ |
|
|
|
|
 |
|
|
商 |
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
実 |
 |
 |
 |
|
 |
 |

|
 |
 |
 |

|

|
法 |
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
廉 |
|
|
|
|
|
|
|
|
|
|
|
 |
隅 |
|
|
|
|
593x^2{593(a^2+b^2+c^2+2ab+2bc+2ca)}より・・・593a^2 を求める
⑤ 「商」の200^2と「廉」の593を掛けて「廉」を 23720000 に置き換える。。
⑥ 「廉」の23720000 を[実」に加える。 -43648432.125 + 23720000 = -19928432.125
★「実」を -19928432.125 に置き換える。
| 千万 |
百万 |
十万 |
万 |
千 |
百 |
十 |
一 |
分 |
厘 |
毛 |
糸 |
|
| ⑦⑧ |
|
|
|
|
 |
|
|
商 |
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
実 |
 |
 |
 |
|
 |
 |

|
 |
 |
 |

|

|
法 |
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
廉 |
|
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
隅 |
|
|
|
|
⑦ 1X^3 1{a^3+b^3+c^3+3ab(a+b)+3bc(b+c)+3ca(c+a)+6abc}・・・1a^3 を求める
●「商」の200^3 と「隅」の1を掛けて「隅」を 8000000 に置き換える
●「隅」の8000000を[実」に加える。 -19928432.125 + 8000000 = -11928432.125
★「実」を -11928432.125 に置き換える。 -11928432.125
⑧ 百の位は終了です。 「商」十の位を予想して計算します。
a^3+b^3+c^3+3ab(a+b)+3bc(b+c)+3ca(c+a)+6abc ・・・a^3+b^3・3ab(a+b) を求める
+593(a^2+b^2+c^2+2ab+2bc+2ca) ・・・593(a^2+b^2+2ab) を求める
- 87912.25(a+b+c) - 26065982.125 = 0・・・- 87912.25(a+b) を求める
b^3 = 40だと a^3+b^3 より 200^3+40^3 = 8064000 3ab(a+b) = 3×200×40(240) = 5760000
593(a^2+b^2+2ab) より 593(200^2+40^2) = 24668800 593×2ab = 593×2×200×40 = 9488000
- 87912.25(a+b) より - 87912.25(200+40) = -21098940
8064000+5760000+24668800+ 9488000-21098940 = 26881860
26881860 は 26065982.125を、超えた為、「商」の十の位を 3 とします。
| 千万 |
百万 |
十万 |
万 |
千 |
百 |
十 |
一 |
分 |
厘 |
毛 |
糸 |
|
| ⑨ |
|
|
|
|
 |
 |
|
商 |
|
|
|
|
 |
 |
 |
 |
 |

|
 |
 |
実 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |

|
法 |

|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
廉 |
|
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
隅 |
|
|
|
|
⑨- 87912.25x{- 87912.25(a+b+c)}より・・・- 87912.25b を求める
-87912.25 ×30 = -2637367.5
● -2637367.5 を[法」に加える。 -17582450 +(-2637367.5) = -20219817.5 を「法」とする。
●「法」の -20219817.5 を[実」に加える。 -11928432.125 +( -20219817.5) = -32148249.625
★「実」を -32148249.625 に置き換える。
| 千万 |
百万 |
十万 |
万 |
千 |
百 |
十 |
一 |
分 |
厘 |
毛 |
糸 |
|
| ⑩⑪ |
|
|
|
|
 |
 |
|
商 |
|
|
|
|
| |
|
 |
 |
 |
 |
 |
 |
実 |
 |
 |
 |
|
 |
 |

|
 |
 |
 |
 |

|
法 |

|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
廉 |
|
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
隅 |
|
|
|
|
593(200^2+30^2+7^2+2×200×30+2×30×7+2×7×200)=33308217
23720000+7649700{31369700}
⑩ 593x^2{593(a^2+b^2+c^2+2ab+2bc+2ca)}より・・・593(b^2+2ab) を求める
● 593(b^2+2ab) を求める
593 × 30^2 = 533700 593(2×200×30) = 7116000 533700+7116000=7649700
● 7649700 を「廉」と[実」に加える。 7649700+ 23720000 = 31369700 を「廉」とする。
-32148249.625 + 31369700 = -778549.625 を「実」とする。
| 千万 |
百万 |
十万 |
万 |
千 |
百 |
十 |
一 |
分 |
厘 |
毛 |
糸 |
|
| ⑫ |
|
|
|
|
 |
 |
|
商 |
|
|
|
|
| |
 |
 |
 |
 |
 |
 |
 |
実 |
 |
 |
 |
|
 |
 |

|
 |
 |
 |
 |

|
法 |

|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
廉 |
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
隅 |
|
|
|
|
200^3+30^3+7^3+3×200×30(200+30)+3×30×7(30+7)+3×7×200(7+200)+6×200×30×7=13312053
a^3 + b^3 + c^3 + 3ab(a+b) + 3bc(b+c) + 3ca(c+a) + 6abc
8000000+ 4167000+1145053=13312053
- 87912.25(200+30+7)=-20835203.25
593(200^2+30^2+7^2+2×200×30+2×30×7+2×7×200)=33308217
200^3+30^3+7^3+3×200×30(200+30)+3×30×7(30+7)+3×7×200(7+200)+6×200×30×7=13312053
a^3 + b^3 + c^3 + 3ab(a+b) + 3bc(b+c) + 3ca(c+a) + 6abc
⑫ X^3{a^3+b^3+c^3+3ab(a+b)+3bc(b+c)+3ca(c+a)+6abc}・・・b^3+3ab(a+b) を求める
● b^3+3ab(a+b) を求める
30^3 = 27000 3ab(a+b) = 3×200×30(200+30) = 4140000 27000 + 4140000 = 4167000
● 4167000 を「隅」に加える。 8000000 + 4167000 = 12167000
● 4167000 を「実」に加える。 -778549.625 + 4167000 = 3388450.375
⑬ 十の位は終了です。 「商」一の位を予想して計算します。
x^3 + 593x^2 - 87912.25x - 26065982.125 = 0 の展開式
a^3 + b^3 + c^3 + 3ab(a+b) + 3bc(b+c) + 3ca(c+a) + 6abc +
593(a^2+b^2+c^2+2ab+2bc+2ca)- 87912.25(a+b+c) - 26065982.125 =0
■ a=200 b=30 c=8 とすると ■
a^3 + b^3 + c^3 + 3ab(a+b) + 3bc(b+c) + 3ca(c+a) + 6abc +
593(a^2+b^2+c^2+2ab+2bc+2ca)- 87912.25(a+b+c)=26148048.5 となり 26065982.125 を超える為
c=7 とします。
| 千万 |
百万 |
十万 |
万 |
千 |
百 |
十 |
一 |
分 |
厘 |
毛 |
糸 |
 |
| ⑭ |
|
|
|
|
 |
 |

|
商 |
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
実 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
法 |

|
 |
|
|
 |
 |
 |
 |
 |
 |
 |
 |
廉 |
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
隅 |
|
|
|
|
⑭ - 87912.25x{- 87912.25(a+b+c)}より・・・- 87912.25c を求める
-87912.25 ×7 = -615385.75
● -615385.75 を[法」に加える。 -20219817.5+(-615385.75) = -20835203.25 「法」とする。
●「法」の -20835203.25 を[実」に加える。 3388450.375 +(-20835203.25) = -17446752.875
★「実」を -17446752.875 に置き換える。
| 千万 |
百万 |
十万 |
万 |
千 |
百 |
十 |
一 |
分 |
厘 |
毛 |
糸 |
|
| ⑮ |
|
|
|
|
 |
 |

|
商 |
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
実 |
 |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
法 |

|
 |
|
|
 |
 |
 |
 |
 |
 |
 |
 |
廉 |
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
隅 |
|
|
|
|
593(200^2+30^2+7^2+2×200×30+2×30×7+2×7×200)=33308217
23720000+7649700{31369700+1938517
⑮ 593x^2{593(a^2+b^2+c^2+2ab+2bc+2ca)}より・・・593(c^2+2bc+2ca) を求める
● 593(c^2+2bc+2ca) を求める
593 × 7^2 = 29057 593(2×30×7) = 249060 593(2×7×200)=1660400
29057+ 249060+1660400=1938517
● 1938517 を「廉」と[実」に加える。 1938517 + 31369700 = 33308217 を「廉」とする。
-17446752.875 + 33308217 = 15861464.125 を「実」とする。
| 千万 |
百万 |
十万 |
万 |
千 |
百 |
十 |
一 |
分 |
厘 |
毛 |
糸 |
|
| ⑯ |
|
|
|
|
 |
 |

|
商 |
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
実 |
 |

|
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
法 |

|
 |
|
|
 |
 |
 |
 |
 |
 |
 |
 |
廉 |
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
 |
隅 |
|
|
|
|
⑯ X^3{a^3+b^3+c^3+3ab(a+b)+3bc(b+c)+3ca(c+a)+6abc}・・・c^3+3bc(b+c)+3ca(c+a)+6abc を求める
● c^3+3bc(b+c)+3ca(c+a)+6abc を求める
7^3+3×30×7(30+7)+3×7×200(7+200)+6×200×30×7 = 1145053
● 1145053 を「隅」に加える。 12167000 + 1145053 = 13312053
● 4167000 を「実」に加える。 15861464.125 + 13312053 = 29173517.125
「実」が、 26065982.125 を超えたので、余り有です。
余りは、29173517.125 - 26065982.125 = 3107535
⑬ 「実」が 0 になり計算終了です。答えは、23 です。