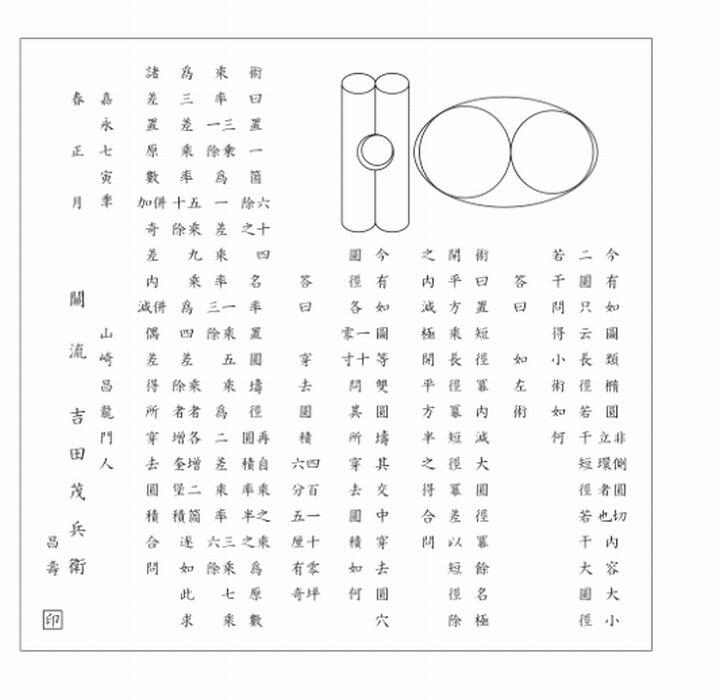
伊佐爾波神社（いさにわじんじゃ）　【 嘉永7年(1850)正月　山崎昌竜門人吉田茂兵衛昌寿　奉納 

｛原文｝　　　　　 　非側圓切

  今有如圓類楕圓立環者也内容大小二圓只云長

  整数スル事ヲ欲ス各球径幾何ヲ得ル術如何ナルヤ

　答　如左術

 　

 術曰 多少両位ヲ設ケ多少差羃 ヲ置キ多少相乗ヲ加入シ大球径ナリ天因少数黄球径トス多少差ヘ多少相乗ヲ載シ

赤球径ナリ合問 

｛原文の要訳｝

吉田茂兵衛の算額は、２つの問題からなっている。左の問題は、円柱を２つ並べて、それと同じ大きさの円柱を垂直に

貫通させて、抜き取った立体の体積を求める問題である。ここでは、右の類楕円の問題を取り上げます。

 類楕円（楕円ではなく ※トーラス｛補足｝を切ったもの）内に大小２個の円がある。類楕円の直径、短径、大円の直径の長さが与えられたとき、小円の直径を求めよ。

　※トーラス｛補足｝　

 平面上の円と（円と交わらない）直線があるとき， 直線の周りに円を1回転して得られる曲面がトーラス 

（ドーナツ，浮き輪） である． 。

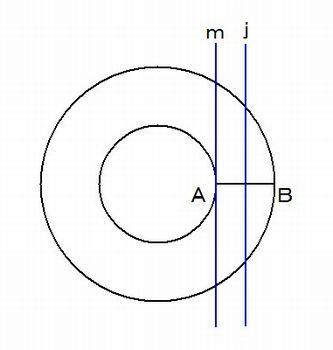
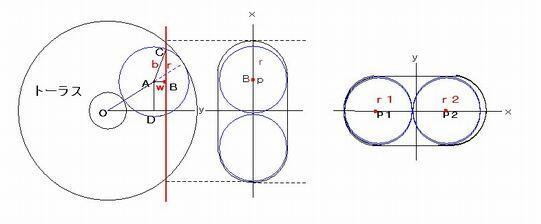
トーラスを回転軸の上方から見た、下図において、直線 ｊ （トーラスの幅 ＡＢ の中心を通り ＡＢ と垂直な直線) の位置の

切断面で切ったものを 「類楕円」 または 「環楕円」 と和算では呼んでいる。

　　　　　

　 　【楕円の方程式の標準形】

■　a>b>0 のとき，方程式

■楕円の定義（標準形）

平面上の２つの点F1とF2からの距離の和が一定である点Pの軌跡を楕円と言い、この２つの点F1とF2のことを

楕円の焦点と言います。 

楕円の方程式（標準形）は　x^2/a^2+y^2/b^2=1　（ただしa＞ｂ＞０） と表される．

で表わされる曲線は，下図のような楕円になる。 楕円の方程式の標準形という．

  _____________

焦点F'1の座標：   (-ｆ，０)=(-√a^2-b^2,0)

  ___________

焦点 Ｆ2の座標： (ｆ，０)=(√a^2-b^2,0)

長軸の長さ： 2a 短軸の長さ： 2b となる．

■楕円の方程式の証明

条件よりPF+PF'=2a　・・・�@ 

  _____________________ ___________________

ＰＦ＝√（ｘ−ｃ）^2＋ｙ^2　　　　ＰＦ'＝√（ｘ＋ｃ）^2＋ｙ^2

よって�@は次のように変形できます。 

 _____________________ _____________________ 

√（ｘ−ｃ）^2＋ｙ^2+√（ｘ＋ｃ）^2＋ｙ^2=2a　

 これを変形して 、

 _____________________ ___________________

√（ｘ−ｃ）^2＋ｙ^2＝2a−√（ｘ＋ｃ）^2＋ｙ^2

両辺を２乗して整理していきます。 

  _____________________ _____________________

（√（ｘ−ｃ）^2＋ｙ^2）^2＝（2a−√（ｘ＋ｃ）^2＋ｙ^2）^2

  ____________________   

 ｘ^2−２ｃｘ＋ｃ^2＝４ａ^2−４ａ√（ｘ＋ｃ）^2＋ｙ^2＋ｘ^2＋２ｃｘ＋ｃ^2

  ___________________

４ａ√（ｘ＋ｃ）^2＋ｙ^2＝４ａ^2＋４ｃｘ

  ____________________

ａ√（ｘ＋ｃ）^2＋ｙ^2＝ａ^2＋ｃｘ

 ここでまた両辺を２乗して整理します。 

  ____________________

（ａ√（ｘ＋ｃ）^2＋ｙ^2）^2＝（ａ^2＋ｃｘ）^2

ａ^2（ｘ＋ｃ）^2＋ａ^2ｙ^2＝ａ^４＋２ａ^2ｃｘ＋ｃ^2ｘ^2

ａ^2ｘ^2＋２ａ^2ｃｘ＋ａ^2ｃ^2＋ａ^2ｙ^2＝ａ^４＋２ａ^2ｃｘ＋ｃ^2ｘ^2

ａ^2ｘ^2−ｃ^2ｘ^2＋ａ^2ｙ^2＝ａ^４−ａ^2ｃ^2

ｘ^2（ａ^2−ｃ^2）＋ａ^2ｙ^2＝ａ^2（ａ^２−ｃ^2）・・・�A 

  _____________

a＞cより　 √ａ^２−ｃ^2＝ｂ　とおくと、 

a＞ｂ>0より　ａ^２−ｃ^2＝ｂ^2　なので�A式は 

 ｂ^2ｘ^2＋ａ^2ｙ^2＝ａ^2ｂ^2　　両辺を　ａ^2ｂ^2　で割ると 

 

x^2/a^2+y^2/b^2=1　であることが求まります。 

                 

｛計算方法｝　　　

  　【現代の計算方法】

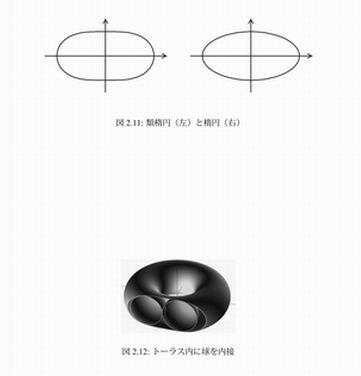
 類楕円と楕円の形状の比較で、類楕円の長軸の先は楕円のようにはとがってはなく丸くなっている。

  【類楕円の４次方程式】

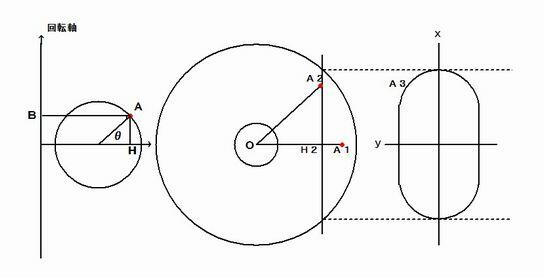
 図は切断面としての類楕円である。類楕円の短軸が2b となるためには、左側の図において回転円の半径がb

でなければならない。類楕円の長軸が2a となるためには、中央の図において、切断面を表す直線が円によって

切り取られる部分の長さが2a とならなければならない。

従って、3 辺a, d, b + d からなる直角三角形に三平方の定理を用いると、

 ｄ^2 = (ｄ + ｂ)^2 - ａ^2 = ｄ^2 ＋２ｂｄ + ｂ^2 - ａ^2　　より ２ｂｄ = ｄ^2 - ｄ^2 - ｂ^2 - ａ^2 = - ｂ^2 + ａ^2  

 　　　  ∴ ｄ = (ａ^2- ｂ^2)/2ｂ 

           

回転円の中心を通る水平方向の軸とのなす角をθとする。

このときAB = d + b cos θ、AH = b sin θ である。この点A は,下の図では点A1 にあたる。

点A1 を回転軸の周りを回転させ、切断面にぶつかったところが点A2 である。

  ____________________________ _________________________________ _______________________________________

このとき、A2H2 =√ (d + b cos θ)2 - d2 = √2bd cos θ + b2 cos2 θ = √(a2 - b2) cos θ + b2 cos2 θ

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ＿＿＿＿＿＿＿＿＿＿＿＿

である。下の図で点A2 に対応するものが点A3 であり、その座標は(√(a2 - b2) cos θ + b2 cos2 θ, b sin θ)

 である。 以上より類楕円のパラメータ表示は

  ______________________________________

x =√(a2 - b2) cos θ + b2 cos2 θ y = b sin θである。

この式からsin2 θ + cos2 θ = 1 を利用して、sin θ, cos θ を消去すると、類楕円の方程式

 類楕円の長軸の長さ： 2a 短軸の長さ： 2b とする．

　ｂ^2(ｘ^2 + ｙ^2 - ｂ^2)^2 + (ａ^2 - ｂ^2)^2(ｙ^2 - ｂ^2) = ０ ・・・・ で, 類楕円は4 次代数曲線 が得られる。

             

      

  【類楕円の内接円を計算する】

 トーラス内に半径ｂの球を内接させる。 トーラスに内接する球の中心をＡとする。

Ａから切断面に下ろした垂線の足をＢとすると、Ｂは球を切断面で切った切り口の円の中心である。

切断面における点Ｂの座標を(ｐ,０)とし、半径をｒとする。 ＯＡ = d とおくと、　ｄ = (ａ^2 - b^2）/(2ｂ)である。

  ______________

また、ＡＢ = ｗ とおくとき、直角三角形 ＣＡＢにおいて、 ｗ = √ｂ^2 - ｒ^2　である。また直角三角形 ＡＯＤ において　

  ______________________ ________________

ｐ = √ｄ^2 - (ｄ - ｗ)^2 = √2ｄｗ - ｗ^2　である

 

 上図において、長軸 ２ａ で短軸 ２ｂ の類楕円に内接する円の中心の座標を(ｐ,Ｏ)とし半径をｒとするとき

  ______________ 　　 _______________

　　　ｄ = (ａ^2- ｂ^2)/2ｂ　　　ｗ = √ｂ^2 - ｒ^2　　　ｐ = ±√2ｄｗ - ｗ^2

類楕円に内接する円の中心の座標を(ｐ1,Ｏ) , (ｐ2,Ｏ) とし、それぞれの半径を ｒ1 , ｒ2 とする。

このとき、 ｒ1 から ｒ2　を求めるためには、以下の連立方程式　を求める。

　　　　　　　　　　　　　　ｄ = (ａ^2- ｂ^2)/2ｂ　 ・・・�@

　　　　　　　　　　　　　　　 　　 _______________

　　　　　　　　　　　　　　ｗ1 = √ｂ^2 - ｒ1^2　　 ・・・�A

  __________________

　　　　　　　　　　　　　　ｐ1 = √2ｄｗ1 - ｗ1^2　・・・�B

　　　　　　　　　　　　　　　 　 ________________

　　　　　　　　　　　　　　ｗ2 = √ｂ^2 - ｒ2^2　　　・・・�C

  __________________

　　　　　　　　　　　　　　ｐ2 = √2ｄｗ2 - ｗ2^2　 ・・・�D

  ｐ2 - ｐ1 = ｒ1 + ｒ2　　 　・・・�E

  �Eより　 ｐ2^2 = (p1 + (ｒ1 + ｒ2))^2 2ｄｗ2 - ｗ2^2 = ｐ1^2 + 2p1(r1 + r2) + (r1 + r2)^2 

 2dw2 - b^2 + r2^2 = 2dw1 - w1^2 + 2p1(r1 + r2) + (r1 + r2)^2

 2dw2 = 2dw1 - ｂ^2 + ｒ1^2 + 2p1(r1 + r2) + (r1 + r2)^2 + b^2 - r2^2 

 2dw2 = 2dw1 + ｒ1^2 + 2p1(r1 + r2) + r1^2 + 2r1r2 + r2^2 - r2^2 

 2dw2 = 2dw1 + 2r1^2 + 2p1(r1 + r2) + 2r1r2 dw2 = dw1+ r1^2 + p1(r1 + r2） + r1r2  

 ∴ dw2 = dw1 + (r1 + r2)(p1 + r1)　　　　　

が得られ、両辺を平方して �A と �C を代入し整理すると、

 dw2^2 =(dw1 + ( r1 + r2)(p1 + r1))^2 = (dw1^2 + 2dw1*( r1 + r2)(p1 + r1)) + (( r1 + r2)(p1 + r1)^2 　　　　　　　d^2(b^2 - r2^2) = d(b^2 - r1^2) + 2dw1( r1 + r2)(p1 + r1)) + (( r1 + r2)(p1 + r1)^2 　　　　　

d^2(r1^2 - r2^2) = 2dw1(r1 + r2)(p1 + r1) + (r1 + r2)^2(p1 +r1)^2

となる、ここで、両辺を(r1 + r2) で割って整理することで、

d^2(r1^2 - r2^2) = 2dw1(r1 + r2)(p1 + r1) + (r1 + r2)^2(p1 +r1)^2

d^2(r1 - r2)(r1 + r2)／(r1 + r2) = (2dw1(r1 + r2)(p1 + r1) + (r1 + r2)^2(p1 +r1)^2)／(r1 + r2)

d^2(r1 - r2) = 2dw1(p1 + r1) + (r1 + r2)(p1 +r1)^2

r1d^2 - r2d^2 = 2dw1(p1 + r1) + (r1 + r2)(p1 +r1)^2 

- r2d^2 = 2dw1(p1 + r1) + (r1 + r2)(p1 +r1)^2 - r1d^2 

 r2d^2 = -(2dw1(p1 + r1) + r1(p1 +r1)^2 + r2(p1 +r1)^2 - r1d^2) 

 r2(d2 + (p1 + r1)2) = r1(d2 - (p1 + r1)2) - 2dw1(p1 + r1)

  ∴ ｒ2 = (ｒ1(ｄ^2 - ( ｐ1 + ｒ1)^2) - 2ｄｗ1 ( ｐ1 + ｒ1))/(ｄ^2 + ( ｐ1 + ｒ1)^2)