薬師寺
【薬師寺(やくしじ) 明治21年(1888年)】
{原文}
大球ノ内赤球六個容レ其上ニ黄球ヲ載ス只云各球径整数スル事ヲ欲ス各球径幾何ヲ得ル術如何ナルヤ
答 如左術
術曰 多少両位ヲ設ケ多少差羃 ヲ置キ多少相乗ヲ加入シ大球径ナリ天因少数黄球径トス多少差ヘ多少相乗ヲ載シ
赤球径ナリ合問
{原文の要訳}
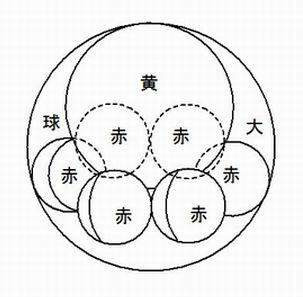
大球の内に赤球6つが接するようにあり、その上に黄球が載っている。
ここで、それぞれの球の直径が整数値になるようにしたい。その整数値を得る方法はどのようであるか。
計算方法 大小2数を設定し、その大小2数の差を2乗した数に、大の数と小の数とを掛け合わせた数を足した数を
天と名づける。天に大の数を掛けた数が大球の直径である。天に小の数を掛けた数が黄球の直径である。
大小2数の差に大の数と小の数とを掛け合わせた数が赤球の直径である。
【整数とは (知恵蔵の解説)
1から始まり1ずつ増える数列1、2、3、4、5……に属する数を自然数という。
これに0とマイナス自然数を合わせた数列……-3、-2、-1、0、1、2、3、4……に属する数を整数という。
2で割れる整数が偶数、2で割れない整数は奇数という。
大球の直径を m、黄球の直径を k、赤球の直径を j とする。整数 a,b(a>b) を設定する。
m = aH k = bH j = ab(a-b) とする。 但し、H = (a-b)^2 + ab とする。
【現代の計算方法】
黄球を K(k)、赤球を J(j),大球を M(m) とする。
この3球の直径の比を m : k : j = a : b :x
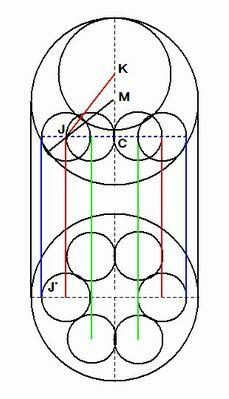
直角三角形 KJC において KJ^2 = JC^2 + KC^2 = JC^2 + (KM + MC)^2
__________________________
KM = (a - b)/2 MC^2 = JM^2 - JC^2 = ((a -x)/2)^2 - x^2 MC = √((a -x)/2)^2 - x^2)
_________________________
(KM + MC)^2 = ((a - b)/2 + √((a -x)/2)^2 - x^2))^2 =
_______________________
(a^2 -2ab +b^2)/4 + 2(a - b) √((a - x)/2)^2 - x^2 + ((a -x)/2)^2 - x^2)) =
___________________________________
(a^2 -2ab +b^2)/4 + 2(a - b) √((a^2 -2ax +x^2) - 4x^2)/4 + (a^2 -2ax +x^2)/4 - x^2)) =
__________________________________ _
(b^2 + 2bx^2 + x^2)/4 = (a^2 -2ab +b^2)/4 + (a - b) √((a^2 -2ax +x^2) - 4x^2) + (a^2 -2ax +x^2)/4
- x^2)) =
__________________________________ _
(b^2 + 2bx^2 + x^2) = (a^2 -2ab +b^2) + 4(a - b) √((a^2 -2ax +x^2) - 4x^2) + (a^2 -2ax +x^2) - x^2) =
(b^2 + 2bx^2 + x^2) = 4x^2 + (a^2 -2ab +b^2) + 2a - b) √((a^2 -2ax +x^2) - 4x^2) + (a^2 -2ax +x^2) - 4x^2
2bx + 2ax + 2ab - 2a^2 = 2(a - b) (√a^2 - 2ax - 3x^2)
2(bx + ax + ab - a^2)/2 = 2/2(a - b)(√(a^2 - 2ax - 3x^2)
(bx + ax + ab - a^2) = (a - b)(√(a^2 - 2ax - 3x^2)
(a + b)x - a(a - b) = (a - b)(√a^2 - 2ax - 3x^2)
((a + b)x - a(a - b))^2 = ((a - b)(√a^2 - 2ax - 3x^2))^2
(a + b)^2x^2 - 2a(a^2 - b^2)x + a^2(a - b)^2 = (a^2 -2ab +b^2)(a^2 - 2ax - 3x^2)
(a^2 + 2ab +b^2 + 3a^2 - 6ab + 3b^2)x^2 - 2a(a^2 - b^2 - a^2 + 2ab - b^2)x +
a^2(a^2 - 2ab + b^2 - a^2 + 2ab - b^2) = 0
(4a^2 - 4ab + 4b^2)x^2 - 2a(2ab - 2b^2)x = 0
x = ab(a - b)/(a^2 -2ab +b^2) = ab(a - b)/(a^2 - 2ab + b^2 + ab)
x = ab(a - b)/((a - b)^2 + ab)
m : k : j = a : b :x = a : b :ab(a - b)/((a - b)^2 + ab)
(a - b)^2 + ab = H として = aH : bH : ab(a - b)
a, b, H は、それぞれ整数値であるから
m =aH k =bH j =ab(a - b)