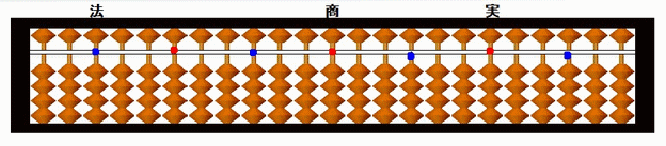
そろばん
【そろばん 開平計算】
◆「算法闕疑抄」第2巻「開平法(平方根の値を求める方法)」に記載された例題◆
寸(1寸=約 30.303 mm)単位の面積が 151.29坪(1坪=約3.305 78m2)ある。
これを開平すれば一辺の長さは、いかほどか?
■そろばん上の表記■
「法」・・・分母の数にあたるもの。
「商」・・・割り算の結果。
「実」・・・分子の数にあたるもの。
■例題の術(方法・手段)■
①実に 151.29 と置く{「「小数点を基準」にして「2 桁ずつ」区切っていく。1¦51¦29 となる}。 位を見て
②まず百の位の1より 「一の位の商 10寸(一尺)」が立つ。
③10×10=100 を実より引く
④「二の位の商 2」が立つ。法に「一の位の商 10」を2倍にして置く、 20 となる。
⑤これに「二の位の商 2」を加え 法を 22 とする。
⑥「一の位の法 20」 を2倍して実より引く・・・ 20×2=40 を実より引く。
⑦「二の位の法 2」 を2倍して実より引く・・・ 2×2=4 を実より引く。 実の残りは 7.29。
⑧「三の位の商 0.3」が立つ。法に「一二の位の商一尺二寸」を2倍にして 24 を法に置く。
⑨法に、いま立てた 0.3 を加え 24.3 とする。
⑩20×0.3=6 を実より引く
⑪4×0.3=1.2 を実より引く
⑫0.3×0.3=0.09 を実より引く。 実が 0 になり 商の 12.3 寸が、求める解です。
【開平法】
開平法の本質は以下の代数式展開ができるところにある。
(a+b+c+d+・・・・・・)2=(a+b+c+d+・・・・・・・)(a+b+c+d+・・・・・・・)
=a2+2ab+2ac+2ad+2ae+・・・・
+b2+2bc+2bd+2be+・・・・
+c2+2cd+2ce+・・・・
+d2+2de+・・・・
+e2+・・・・
=a2+b(2a+b)
+c{2(a+b)+c}
+d{2(a+b+c)+d}
+e{2(a+b+c+d)+e}
+・・・・・
【開平法で検証する】
_____
√ 151.29 の値を開平法で計算する.
① 151.29 をルートの中に書き,「小数点を基準」にして「2 桁ずつ」区切っていく.
また,横にスペースをとっておく.
② 一番左の数は1で 2乗して1 を超えない最大の数 1を,図のように3 ヶ所に書く.
__1¦_____ ¦_____ 1
√ 1¦51.¦29 1
③(1× 1) = 1 を 1の下に書き,1から 1を引く.
そして,51 を下に下ろす.また,その横で 1+ 1= 2 を計算する.
__1¦_____ ¦_____ 1
√ 1¦51.¦29 1
1 ___
ーーーー 2 (1+ 1= 2)
0 51.
④ 「2?」に「?」を掛けて「51」を超えない,最大の 1 桁の整数 ? を求める.
2 2× 2 = 44 ≦ 51 < 23× 3 = 69
であるので,? は 2 これを 3 ヶ所に書き込む
__1¦__2_ ¦_____ 1
√ 1¦51.¦29 1
1 ___
ーーーー 22 (1+ 1= 2)
0 51. 2
⑤ 2 2× 2 の結果44 を 51の下に書き, 51から引く.そして,24を下に下ろす.さらに,
小数点を打つ.また,61 + 1 を横で計算しておく.
__1¦__2_ ¦_____ 1
√ 1¦51.¦29 1
1 _____
ーーーー 22 (1+ 1= 2)
0 51. 2
44 _____
___________ 24 (22 + 2 = 24)
7
⑥ 「24?」に「?」を掛けて「729」を超えない,最大の 1 桁の整数 ? を求める.
243× 3 = 729 ≦ 729 < 244 × 4 = 976
より ? は 3 であり,729 -243× 3 = 729 = 0 なので計算は完了.
= 12.3 とわかる.
__1¦__2_ ¦__3___ 1
√ 1¦51.¦29 1
1 _____
ーーーー 22 (1+ 1= 2)
0 51. 2
44 _____
____________________ 24 (22 + 2 = 24)
7 ¦29 3
7 ¦29
ーーーーーーー
0