丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
棳悈嶼
丂丂丂
丂棳悈嶼偼丄慏偑愳側偳偺棳傟偺偁傞応強傪傪忋傝壓傝偡傞応崌偵娭偟偰丄懍搙丄帪娫丄嫍棧側偳傪梡偄偰弌戣偝傟偨
梫慺偵偮偄偰夝摎偡傞嶼弍偱偡丅
丂嘆丂慏偑忋傞応崌偺懍搙=惷悈偱偺慏偺懍搙-棳傟偺懍搙
丂嘇丂慏偑壓傞応崌偺懍搙=惷悈偱偺慏偺懍搙+棳傟偺懍搙
丂嘊丂惷悈偱偺慏偺懍搙=(壓傝偺懍搙+忋傝偺懍搙)亐2
丂嘋丂棳傟偺懍搙=((壓傝偺懍搙-忋傝偺懍搙)亐2
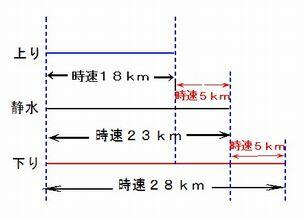
侾丏 偁傞慏偑愳傪忋傞偺偵帪懍侾俉km丄壓傞偺偵帪懍俀俉km偱恑傒傑偟偨丅
丂丂偙偺慏偺惷悈帪偺懍偝偲愳偺棳傟偺懍偝傪媮傔側偝偄丅
夝愢丗 壓偺恾偺傛偆側慄暘恾傪嶌偭偰峫偊傟偽丄惷悈帪偱帪懍俀俁km丄愳偺棳傟偺懍偝偼帪懍俆km丅
夝摎丗惷悈帪乧帪懍俀俁km丂愳偺棳傟偺懍偝乧帪懍俆km
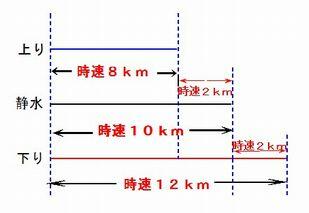
俀丏 偁傞慏偑俁俇km偺愳傪忋傞偺偵俇帪娫偐偐傝傑偡丅偙偺愳偺棳傟偺懍偝偑帪懍俀km偲偡傞偲丄
丂丂壓傝偵壗帪娫偐偐傝傑偡偐丅
夝愢丗 忋傝偺懍偝偼帪懍俇km丅壓偺恾偺傛偆側慄暘恾傪嶌傟偽丄
丂丂丂丂壓傝偼帪懍侾侽km偲側傝丄壓傝偵偐偐傞帪娫偼俁俇亐侾侽亖俁丏俇帪娫乮俁帪娫俁俇暘乯丅
夝摎丗3帪娫俁俇暘
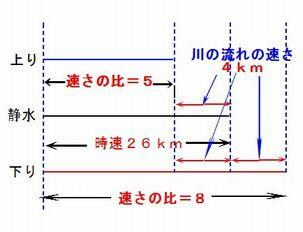
俁丏 惷悈帪偱偺懍偝偑帪懍26偺慏偑偁傝丄偙偺慏偑偁傞愳傪忋傞偺偵侾帪娫俀侽暘丄壓傞偺偵俆侽暘偐偐傝傑偟偨丅
丂丂偙偺愳偺棳傟偺懍偝偼帪懍壗km偱偡偐丅
夝愢丗 偙偺慏偺忋傝偲壓傝偺懍偝偺斾偼丆帪娫偺斾偲媡斾偡傞偺偱丄俆丗俉丅
丂丂忋傝偺懍偝偲壓傝偺懍偝傪懌偟偰2偱妱傞偲惷悈帪偺懍偝偵側傞偺偱俇丏俆偱帪懍俀俇km丅
丂丂惷悈帪偺愳偺棳傟偺懍偝偼丂丂俀俇亐俇丏俆亖係偱
夝摎丗帪懍4km
係丆帪懍侾俉km乮惷悈帪偺僗僺乕僪乯偺懍偝偱恑傓慏偑丄帪懍俇km偱棳傟偰偄傞愳傪丄侾俀侽km壓傞偺偵昁梫側帪娫偼
丂壗帪娫偱偟傚偆偐丠
夝愢丗 慏偼侾俀侽km壓傞偺偱丄丂侾俉km亄俇km亖俀係km偑侾帪娫偱恑傓嫍棧偲側傝傑偡丅
丂丂丂侾俀侽km壓傞偺偵昁梫側帪娫偼丂丂侾俀侽亐俀係亖俆丂丂丂丂丂丂丂夝摎丗俆帪娫
俆丆慏偑愳傪係侽km壓傞偺偵偼俆帪娫偐偐傝丄俀俉km忋傞偵偼俈帪娫偐偐傝傑偟偨丅
偙偺慏偺惷悈帪偺懍偝偲愳偺棳傟偺懍偝傪媮傔側偝偄丅
夝愢 慏 偑壓傞応崌偺懍搙亖係侽km丂亐丂俆帪娫丂亖丂帪懍俉km
慏 偑忋傞応崌偺懍搙亖俀俉km丂亐丂俈帪娫丂亖丂帪懍係km
丂 惷悈偱偺慏偺懍搙亖乮帪懍俉km亄帪懍係km乯丂亐丂俀丂亖丂帪懍俇km丂
丂棳傟偺懍搙=乮帪懍俉km亅帪懍係km乯丂亐丂俀 亖丂帪懍俀km
夝摎丗 惷悈帪偺慏偺懍偝偼丂帪懍俇km丂丂丂丂愳偺棳傟偺懍偝偼丂帪懍俀km
丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亂椃恖嶼亃
椃恖嶼乮偨傃傃偲偞傫乯偲偼丄椃恖乮堏摦偡傞恖丆暔乯偺懍搙丄堏摦帪娫丄堏摦嫍棧側偳偵娭偡傞嶼弍偱偡丅
夝偒曽偺婎杮偼丄乽嫍棧亖懍搙亊帪娫乿偱偡丅
椃恖嶼偼丄棧傟傞応崌丄弌夛偆応崌丄捛偄偐偗傞応崌偺3捠傝偵戝暿偝傟傑偡丅
嘆 棧傟傞応崌
丂丒斀懳曽岦
(A偺懍搙+B偺懍搙)亊帪娫=嫍棧
丂丒摨堦曽岦
(A偺懍搙-B偺懍搙)亊帪娫=嫍棧
嘇弌夛偆応崌
嫍棧亐(A偺懍搙+B偺懍搙)=帪娫
嘊捛偄偐偗傞応崌
嫍棧亐(A偺懍搙-B偺懍搙)=帪娫
侾丏俙挰偲俛挰偼侾倠倣棧傟偰偄傑偡丅
丂孼偑俙挰偐傜俛挰偵岦偗偰暘懍侾俀侽倣偱岦偐偄丄摨偠帪崗偵掜偼俛挰偐傜俙挰偵岦偗偰暘懍俉侽倣偱岦偐偄傑偟偨丅
丂孼偲掜偼壗暘屻偵弌夛偆偱偟傚偆偐丠
夝愢丗椃恖嶼乮弌崌嶼乯偺夝偒曽
丂孼偲掜偑弌崌偆偲偄偆偺偼丄孼偲掜偺偁偄偩偺嫍棧偑侽乮僛儘乯偵側傞偲偄偆偙偲偱偡丅
丂弌敪偡傞慜偺孼偲掜偺嫍棧乮俙挰偲俛挰偺嫍棧乯偼侾倠倣亖侾丆侽侽侽倣偱偡丅
丂偦偙偱丄侾暘偛偲偵偙偺嫍棧偑偳偆曄傢傞偐峫偊偰傒傑偡丅
丂孼偼暘懍侾俀侽倣偱恑傫偱偄傞偺偱丄侾暘娫偵侾俀侽倣嫍棧偑弅傑傝傑偡丅
丂掜傕暘懍俉侽倣偱恑傫偱偄傞偺偱丄侾暘娫偵俉侽倣嫍棧偑弅傑傝傑偡丅
丂孼偲掜傪懌偡偲侾俀侽倣亄俉侽倣偱俀侽侽倣弅傑傞偙偲偵側傝傑偡丅
丂擇恖偑弌夛偆帪娫丂亖丂侾丆侽侽侽倣丂亐丂乮丂暘懍侾俀侽倣丂亄丂暘懍俉侽倣丂乯亖俆暘
夝摎丗 俆暘
俀丏 椃恖嶼乮嘆棧傟傞応崌丒摨堦曽岦乯偺夝偒曽
丂俙丆俛擇恖偺椃恖偑丄摨偠応強偐傜摨偠曽岦偵曕偒巒傔傑偟偨丅
丂俙偼暘懍77m偱俛偼暘懍64m偱偡丅35暘屻偵俙偲俛偼丄壗m棧傟偰偄傞偱偟傚偆丅
夝愢丗 俙俛偼摨堦曽岦偵恑傓偺偱丄俙俛娫偺嫍棧偼擇恖偺懍偝偺嵎偵帪娫傪偐偗偰媮傔傞丅
丂丂丂丂(77m/min-64m/min)亊35暘=455m
夝摎丗 455m
俁丏俙偼帪懍48km偱搶傊丄俛偼帪懍57km偱惣傊摨偠応強偐傜摨帪偵弌敪偟傑偡丅
丂2恖偺嫍棧偑336km偵側傞偺偼丄壗帪娫壗暘屻偱偡偐丅
夝愢丗丂俙俛2恖偼丄斀懳曽岦偵恑傓偺偱丄2恖偼懍偝偺榓偩偗棧傟傞偙偲偵側傞丅
丂336km棧傟傞偺偵梫偡傞帪娫偼丄嫍棧傪懍偝偺榓偱妱偭偰媮傔傞偲丄
丂336km亐(48km/h+57km/h)=3.2帪娫
丂0.2帪娫傪暘偵偡傞偲丄
丂0.2帪娫亊60暘=12暘
丂
夝摎丗3帪娫12暘屻
係丏 廃埻偑5210m偺抮偺廃傝傪俙偼屵屻2帪偵弌敪偟丄俛偼偦偺10暘屻偵俙偲偼媡夞傝偱弌敪偟傑偟偨丅
俙偑暘懍62m丄俛偑暘懍73m偺偲偒丄俙偲俛偼壗帪壗暘偵嵞傃弌夛偆偱偟傚偆丅丂
夝愢丗俙偼俛偑弌敪偡傞傑偱偺10暘娫偵丄62m/min亊10暘=620m恑傓丅
丂傛偭偰丄俛偑弌敪偟偰偐傜俙偲嵞夛偡傞傑偱偵2恖偼丄 5210m-620m=4590m偺嫍棧傪弅傔側偗傟偽側傜側偄丅
丂偲偙傠偱丄2恖偼媡曽岦偵恑傫偱偄傞偺偱丄2恖偺懍偝偺榓偩偗嫍棧偑弅傓丅
丂傛偭偰丄2恖偑嵞夛偡傞傑偱偺帪娫偼丄俛偑弌敪偟偰偐傜丄4590m亐(62m/min+73m/min)=34暘屻
丂俙偼屵屻2帪偵弌敪偟丄俛偼偦偺10暘屻偵弌敪偟偨偺偱丄2恖偑嵞夛偟偨帪娫偼丄
丂屵屻2帪+10暘+34暘=屵屻2帪44暘
夝摎丗屵屻2帪44暘
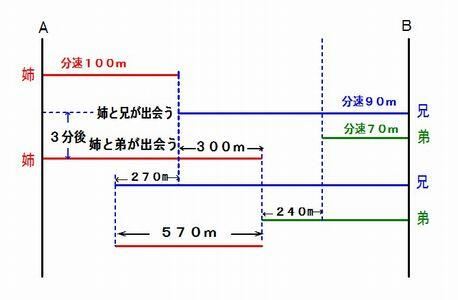
俆丏 巓偼暘懍100m偱A抧揰偐傜B抧揰傊丄孼偲掜偼偦傟偧傟暘懍90m丄暘懍80m偱B抧揰偐傜A抧揰傊摨帪偵弌敪偟傑偟偨丅
搑拞偱巓偲孼偑弌夛偭偰偐傜3暘屻偵巓偲掜偑弌夛偄傑偟偨丅丂AB娫偼壗m偱偡偐
夝愢丗孼偲掜偼丄1暘娫偵10m偺嵎偑弌傑偡丅丂暘懍90m亅暘懍80m亖暘懍侾侽m
丂丂巓偲孼偑弌夛偭偨偁偲偵丄巓偲掜偑弌夛偆偲丄孼偲掜偲偺嫍棧偺嵎偼570m偵側傝丄1暘娫偵10m偺嵎偑偱偒傞偺偱丄丂丂丂
俁恖偑摨帪偵弌敪偟偰偐傜57暘屻偲偄偆偙偲偑傢偐傞丅
丂丂54暘屻偱巓偲孼偺嫍棧偺榓偑AB娫偵側傞偺偱丄AB娫偼乮100亄90乯亊54亖10260m
夝摎丗10260m
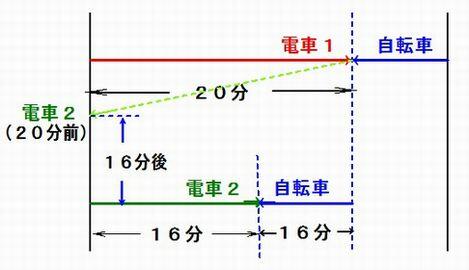
俇丏20暘偍偒偵揹幵偑憱偭偰偄傞慄楬偵暯峴偟偨摴楬偱丄帺揮幵偑帪懍12km偱憱偭偰偄傑偡丅
丂偙偺帺揮幵偼斀懳曽岦偐傜16暘偍偒偵揹幵偲偡傟偪偑偭偰偄傑偡丅揹幵偺懍偝偼帪懍壗km偱偡偐丅
夝愢丗 揹幵1偲帺揮幵偑偡傟偪偑偭偨偲偒偵丄揹幵2偼20暘慜偵偁傝丄16暘屻偵帺揮幵偲偡傟偪偑偆丅
揹幵偑4暘偐偐傞嫍棧傪帺揮幵偑16暘偐偐傞偺偱丄揹幵偲帺揮幵偺懍偝偺斾偼4丗1丅
帺揮幵偑帪懍12km側偺偱丄揹幵偺懍偝偼 帪懍48km丅
夝摎丗帪懍48km
俈丏 廃埻偑5210m偺抮偺廃傝傪俙偼屵屻2帪偵弌敪偟丄俛偼偦偺10暘屻偵俙偲偼媡夞傝偱弌敪偟傑偟偨丅
丂俙偑暘懍62m丄俛丂偑暘懍73m偺偲偒丄俙偲俛偼壗帪壗暘偵嵞傃弌夛偆偱偟傚偆丅丂
夝愢丗 俙偼俛偑弌敪偡傞傑偱偺10暘娫偵丆丂62m/min亊10暘=620m恑傓丅
丂丂傛偭偰丄俛偑弌敪偟偰偐傜俙偲嵞夛偡傞傑偱偵2恖偼丄5210m-620m=4590m偺嫍棧傪弅傔側偗傟偽側傜側偄丅
丂丂偲偙傠偱丄2恖偼媡曽岦偵恑傫偱偄傞偺偱丄2恖偺懍偝偺榓偩偗嫍棧偑弅傓丅
丂丂傛偭偰丄2恖偑嵞夛偡傞傑偱偺帪娫偼丄俛偑弌敪偟偰偐傜丄丂
丂丂4590m亐(62m/min+73m/min)=34暘屻
丂丂俙偼屵屻2帪偵弌敪偟丄俛偼偦偺10暘屻偵弌敪偟偨偺偱丄2恖偑嵞夛偟偨帪娫偼丄
丂丂屵屻2帪+10暘+34暘=屵屻2帪44暘
夝摎丗屵屻2帪44暘