丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂恛崊婰
乽恛崊婰乿偼,姲塱4擭(1627)妏憅堦懓弌恎偺媑揷岝桼(1598-1672)偺 庤偵傛偭偰弌斉 偝傟 偨丅
岝桼偼,栄棙廳擻偵巘帠偟,屻偵仸妏憅慺埩乮偡傒偺偔傜 偦偁傫乯仸偵乽嶼朄摑廆乿(掱戝埵挊,1592擭.僜儘僶儞偺嶼朄傪
愢偄偨拞崙偺嶼彂)傪妛傫偱悢妛偵払偟偨偲偄傢傟傞.丅弶斉偑姲塱4擭偵弌偝傟偨帪,岝桼偼29嵥偱偁偭偨.
偦偟偰,姲暥12擭乮1672)偵杤偡傞傑偱偵廫悢夞傕憹曗,偁傞偄偼夵掶傪廳偹偨丅
丂仸妏憅慺埩乮偡傒偺偔傜 偦偁傫乯仸乮1571乣1632乯 峕屗弶婜偺妛幰丒杅堈壠丅捠徧丄梌堦丅
慺埩偼崋乮偛偆乯徧崋偺棯丅柤傗帤埲奜偵恖傪屇傇嵺偵巊傢傟傞屇傃柤丅
庨報慏杅堈偵廬帠偟偨傎偐丄彅壨愳夵廋偵傕岟傪棫偰偨丅杮垻栱岝墄偵彂傪妛傃丄妏憅棳彂晽偺巒慶偲側傞丅
恛崊婰偺柤慜偺桼棃偼丄暓嫵偺偙偲偽偵乽恛揰崊 (偠傫偰傫偛偆)乿偲偺偑偁傞丅偲偰偮傕側偔挿偄帪娫偺偨偲偊偩丅
偨偲偊偽丄恛揰崊偼丄傢偨偟偨偪偺悽奅傪10壄廤傔偰丄偙傟傪偤傫傇暡(偙側)偵偟偰丄偦偺暡偺堦偮傇偢偮傪暿偺悽奅偺堦偮偢偮偵偮偗偰偄偔丅
偙偺暡偑側偔側偭偨偲偒丄偦偺悽奅傪傑偨暡偵偟偰丄偦偺暡堦偮傇偢偮傪堦崊偲偟偰悢偊偨傕偺偑恛揰崊偱偁傞丅 丂
恛崊偼丄恛揰崊傪偐傫偨傫偵尵偭偨尵偄曽丅恛崊婰偲偄偆柤慜偼丄恛崊偨偭偰傕曄傢傜側偄恀棟偺彂傎傫偲偆偺杮偲偄偆堄枴偱偡丅
乽恛崊婰乿偵婰偝傟偨撪梕偱儐僯乕僋側傕偺偺傂偲偮偼丄乽柦悢朄乮悢偺扨埵乯乿偵娭偡傞抦幆偱偡丅
堦丄廫丄昐丄愮丄枩丄壄丄挍丄嫗乮偗偄乯偁偨傝傑偱側傜丄崱偱傕丄嬥妟偺昞帵傗僐儞僺儏乕僞偺悽奅側偳偱巊傢傟傑偡偑丄10偺20忔偺乽毚乮偑偄乯乿丄
10偺28忔偺乽忰乮偠傚偆乯乿丄10偺32忔偺乽峚乮偙偆乯乿偲側傞偲丄晛抜偼暦偄偨偙偲傕側偄扨埵偱偼側偄偱偟傚偆偐丅
偝傜偵扨埵偼戝偒偔側傝丄乽峆壨嵐乮偛偆偑偟傖乯乿乮10偺52忔乯丄乽垻憁媉乮偁偦偆偓乯乿乮10偺56忔乯丄乽撨桼懠乮側備偨乯乿乮10偺60忔乯丄
乽晄壜巚媍乮傆偐偟偓乯乿乮10偺64忔乯偲丄乽悢偊傜傟側偄乿悢偺悽奅偵側偭偰備偒丄嵟戝偺傕偺偼乽柍検戝悢乿偲側傝傑偡
偪側傒偵丄偙傟傜悢偺扨埵偼拞崙偐傜偒偨傕偺偱丄乽峆壨嵐乿偐傜忋偺扨埵偵偮偄偰偼暓嫵偺宱揟偑桼棃偵側偭偰偄傑偡丅
乽峆壨嵐乿偼乽峆壨乿亖僈儞僕僗愳偺偙偲偱丄僈儞僕僗愳偺嵒偺悢傎偳偺戝偒側悢偲偄偆堄枴偱偡丅
傑偨丄暓嫵偺宱揟偺拞偱偼丄垻栱懮暓偺執戝偝傪昞尰偡傞偨傔偵乽晄壜巚媍岝暓乿偲屇傫偩傝偟傑偡丅
偨偩丄摉帪偺僀儞僪偺悢偺扨埵偺庢傝曽偼尰嵼偲堎側偭偰偍傝丄傑偨宱揟偵傛偭偰悢偺柤徧偑堎側傞偙偲偑偁傝傑偡丅
偪側傒偵丄乽恛崊婰乿偱偼彫偝偄悢偺屇傃曽傕婰偝傟偰偄傑偡丅
乽暘乿乽椥乿乽栄乿乽巺乿乽崥乿乽旝乿乽慇乿乧偲側傫偲側偔嵶偐偦偆側娍帤偑暲傫偱偄偒丄偮偄偵偼乽柾屝乿丄乽鐣弰乿丄乽弖懅乿丄乽檵撨乿丄乽嫊嬻乿丄乽惔忩乿偲丄
偙偪傜傕暓嫵桼棃傜偟偄乽柍乿偺悽奅偵偮側偑偭偰偄偒傑偡丅
媑揷岝桼乮1598亅1672乯偺乽恛崊婰乿偼丄擔杮恖偺悢妛椡傪旘桇揑偵崅傔傞偒偭偐偗偲側偭偨丄悢妛偺弶摍
嫵壢彂偱偡丅姲塱係擭乮1627乯偺弶斉偐傜丄偨偄傊傫側恖婥傪攷偟丄偡偖偵奀懐斉偑懡悢弌斉偝傟傑偟偨丅偦傟偵懳峈
偡傞偨傔傕偁偭偰丄挊幰偺岝桼帺恎偑壗搙偐夵掶斉傪弌偟偰偄傑偡丅
乽恛崊婰乿偵偼丄嬨嬨丒偦傠偽傫摍偺婎杮帠崁傗丄暷偺攧攦丒棙懅寁嶼丒搚抧偺柺愊寁嶼側偳惗妶偵懄偟偨條乆側幚梡揑栤戣偵壛偊偰丄乽宲巕棫偰乿
乽偹偢傒嶼乿側偳偺悢妛僷僘儖揑側栤戣傕懡偔廂榐偝傟丄恖婥傪屇傃傑偟偨丅
岝桼偑庤傪壛偊側偔側偭偨屻傕丄乽仜仜恛崊婰乿乽恛崊婰仜仜乿偲偄偭偨椶帡彂偑峕屗帪戙偐傜柧帯帪戙偵偐偗偰300庬
埲忋傕弌斉偝傟丄乽偫傫偙傆偒乮恛崊婰乯乿偑悢妛偦偺傕偺傪堄枴偡傞傛偆偵側傞傎偳丄恖乆偵恊偟傑傟傑偟偨丅
崱夞偼丄偦偺偆偪偺32庬傪揥帵偟偰偄傑偡丅
傑偨丄岝桼偑嵟屻偵弌斉偟偨姲塱18擭斉乮1641乯偵偼丄偁偊偰夝摎傪嵹偣側偄挧愴栤戣乮偙傟傪堚戣偲屇傃傑偡乯偑12栤宖嵹偝傟傑偟偨丅
偙偺挧愴偵墳偠偨恖偑丄夝摎偲怴偨偵帺暘偑峫偊偨堚戣傪杮偵偟偰弌斉偟傑偟偨丅
偙傟埲崀丄堚戣偵夝摎偟丄怴偨側堚戣傪採帵偡傞偲偄偆宍幃偑棳峴偟丄杮奿揑側悢妛乮榓嶼乯偺敪揥偵戝偒偔婑梌偡傞偙偲偵側傝傑偡丅
仭亀恛崊婰亁偺栤戣仭
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂亂栻巘嶼亃
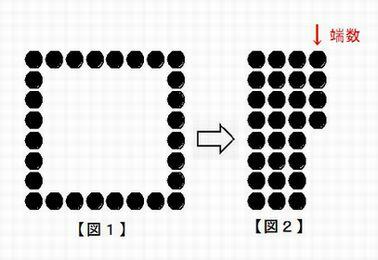
岄愇傪梡偄偨梀傃丅岄愇傪拞嬻惓曽宍忬偵暲傋偝偣丄偦傟傪曵偟偰偐傜夵傔偰堦楍偑傕偲偺堦曈偲摨悢偵側傞傛偆偵懙偊偰暲傋偝偣傞偲丄
嶰楍偵側傝壗屄偐巆傞丅偦偺巆傝偺屄悢偐傜岄愇偺憤悢傪摉偰傞丅偦偺摉偰曽偼乮巆傝偺悢亊4乯亄12 偱偁傞丅偙偙偵昞傟傞堦擇傪栻巘擛棃偺
堦擇偺惥婅丄廫擇恄彨偵側偧傜偊偰栻巘嶼偲偄偆丅乽恛崊婰乿偵婰嵹偑偁傞丅
丂 亂栻巘嶼偺梀傃曽亃
丂偙偺僎乕儉偲偦偺梀傃曽傪師偺売忦彂偒 嘆乣嘋 偱帵偟傑偡丅
嘆丂偼偠傔偵岄愇乮崟乯傪懡悢梡堄偟偰憡庤偵搉偟偰偍偒傑偡丅
嘇丂帺暘偑屻傠岦偒偵側偭偰偄傞娫偵丄嘆偱搉偝傟偨岄愇傪巊偭偰丄塃偺乵恾侾乶偱帵偡傛偆側丄堦曈偑係屄埲忋偺惓曽宍
傪憡庤偵嶌偭偰傕傜偄傑偡丅
嘊丂憡庤偵丄嘇偱嶌偭偨惓曽宍偺堦曈偩偗傪巆偟偰丄偦偺堦曈偵増偭偰乵恾俀乶偺傛偆偵岄愇傪暲傋懼偊偰傕傜偄傑偡丅
嘋丂嵟屻偺楍偺岄愇偺屄悢乮偙傟傪抂悢偲屇傇偙偲偵偟傑偡乯傪憡庤偵嫵偊偰傕傜偆偩偗偱丄帺暘偑巊梡偝傟偰偄傞岄愇偺丂憤悢傪弍幰偑摉偰傞梀傃偱偡丅
亂拲亃丂忋婰偺憖嶌 嘇乣嘋 偺娫偼帺暘偼忢偵屻傠岦偒偺傑傑側偺偱丄帺暘偼乵恾侾乶偲乵恾俀乶傪尒 傞偙偲偼偱偒傑偣傫丅
丂=====================================================================
丂偮偓偵丄栻巘嶼偺梀傃曽偺堦椺傪帵偟傑偡丅
亂梀傃曽偺椺亃
憡庤偑乵恾侾乶偺傛偆側惓曽宍傪嶌偭偰丄偦傟傪乵恾俀乶偺傛偆偵暲傋懼偊傑偡丅偦偟偰丄亀抂悢偼係偱偡丅亁 偲弍幰偵嫵偊偨偲偟傑偡丅
偦偟偰帺暘偼偦傟傪挳偄偰娙扨側寁嶼傪偟偰偐傜丄亀岄愇偺憤悢偼俀俉偱偡丅亁 偲尒帠偵摉偰偰尒偣傑偡丅
亂栻巘嶼 偺巇慻傒亃丂
憡庤偐傜抂悢傪嫵偊偰傕傜偭偨偩偗偱丄偳偆偟偰丄帺暘偼憡庤偑巊梡偟偨岄愇偺屄悢傪摉偰傞偙偲偑偱偒傞偺偱偟傚偆偐丅
偮偓偵丄偦偺巇慻傒傪愢柧偟傑偡丅
丂亂栻巘嶼偺巇慻傒亃
堦曈偺岄愇偺屄悢偑 倣乮倣亞係乯 偱偁傞傛偆側惓曽宍傪嶌傞偺偵昁梫側岄愇偺憤悢傪 倱 丄岄愇傪暲傋捈偟偨偲偒偺抂悢傪 値 偲偟傑偡丅
惓曽宍偺巐嬿偺岄愇 仠 偼擇偮偺曈偵懏偟偰偄傞偺偱丂丂丂丂丂丂丂
丂倱亖係乮倣亅侾乯亖係倣亅係 丒丒丒 嘆
偑惉傝棫偪傑偡丅偟偨偑偭偰丄岄愇傪惓曽宍偺堦曈偵増偭偰暲傋懼偊傞偲丄係楍栚偼偐側傜偢係屄偺晄懌偑惗偠傞偺偱丂
丂丂 倣亖値亄係 丒丒丒 嘇
偑惉傝棫偪傑偡丅偙偙偱丄嘇 傪 嘆 偵戙擖偟偰惍棟偡傞偲丂倱亖係乮値亄係乯亅係亖係値亄侾俀丂偡側傢偪
丂丂丂丂 倱亖係値亄侾俀 丒丒丒 嘊丂丂偑摼傜傟傑偡丅
丂丂丂===============================================================================
慜愡偱帵偟偨 亂梀傃曽偺椺亃 偱偼丄憡庤偑 亀抂悢 値 偼俁偱偡亁 偲弍幰偵嫵偊傑偟偨丅偦傟傪挳偄偰丄弍幰偼忋偺幃嘊傪棙梡偟偰 丂
倱亖係亊係亄侾俀亖俀係 偲寁嶼偟偰偐傜丄亀岄愇偺憤悢偼俀俉偱偡亁 偲摉偰傞偲偄偆傢偗偱偡
丂丂亂栻巘嶼偵偮偄偰偺曗懌亃丂
亂栻巘嶼偺梀傃曽亃偺嘇偱丄乽憡庤偵堦曈偑係屄埲忋偺惓曽宍傪嶌偭偰傕傜偆乿偲偄偆偙偲偵側偭偰偄傑偡丅
偮傑傝丄堦曈偺岄愇偺屄悢 倣 偵 倣亞係 偲偄偆忦審偑偮偄偰偄傑偡丅丒丒丒愢柧偟傑偡丅
偙偙偱丄倣亖侾 偼戣堄偐傜攔彍偝傟偰摉慠偱偡丅偦偟偰丄丂倣亖俀丆俁丆係 偵懳墳偡傞抂悢 値 偲岄愇偺憤悢 倱 偺抣傪媮傔偰傒傞偲丄戣堄偐傜
乵倣亖俀 偺偲偒 値亖侽 丆倱亖係乶 丆 乵倣亖俁 偺偲偒 値亖俀 丆倱亖俉乶 丒丒丒 乵A乶丂
傑偨丄慜愡偺亂栻巘嶼偺巇慻傒亃偺摍幃 倱亖係倣亅係 偲 倣亖値亄係 偐傜
乵倣亖係 偺偲偒 値亖侽 丆倱亖侾俀乶 丆 乵倣亖俇 偺偲偒 値亖俀 丆倱亖俀侽乶 丒丒丒乵B乶
偲側傝傑偡丅偟偨偑偭偰丄乵A乶 偲 乵B乶 偐傜丄 乻 値亖侽 偵懳墳偡傞 倱 偺抣偑 倱亖係丆侾俀 乼 偲 乻 値亖俀 偵懳墳偡傞 倱 偺抣偑 倱亖俉丆俀侽 乼
偺傛偆偵丄値 偵懳墳偡傞 倱 偺抣偑俀屄偁傞偙偲偑傢偐傝傑偡丅
偙偺寢壥丄憡庤偑 亀抂悢 値 偼侽偱偡亁 傑偨偼 亀抂悢 値 偼侽偱偡亁 偲弍幰偵嫵偊偨偲偒偼丄弍幰偼偦偺墳摎偵戝曄崲傞偙偲偵側傝傑偡丅丂
偙偺傛偆側棟桼偐傜丄堦曈偺岄愇偺屄悢 倣 偵 倣亞係 偲偄偆忦審偑偮偄偰偄傞偺偱偡丅
亂栻巘嶼偺堦斒幃亃丂
栻巘嶼偵偼懡偔偺僶儕僄乕僔儑儞偑偁傝傑偡丅
娐拞愬偵傛偭偰彂偐傟偨 亀榓崙抦宐妑亁乮侾俈俀俈擭乯偵偼丄嶰妏宍偵偮偄偰偺栻巘嶼偑嵹偭偰偄傑偡丅
傑偨丄拞崻旻弞偵傛偭偰彂偐傟偨 亀姩幰屼壘憪巻亁乮侾俈係俁擭乯偵偼丄惓屲妏宍偺応崌偺懠偵丄惓倎妏宍偺応崌偵偮偄偰偺堦斒幃偑
摍幃 倱亖倎値亄倎乮倎亅侾乯 偱昞傢偝傟傞偙偲偑婰嵹偝傟偰偄傑偡丅
偙偺摍幃偼丄偮偓偺傛偆偵偟偰摫傃偐傟傑偡丅
丂亂栻巘嶼偺堦斒幃亃
堦曈偺岄愇偺屄悢偑 倣乮倣亞倎乯 偱偁傞傛偆側 惓倎妏宍傪嶌傞偺偵昁梫側岄愇偺憤悢傪倱 丄岄愇傪暲傋捈偟偨偲偒偺
抂悢傪 値 偲偟傑偡丅惓倎妏宍偺嬿偺岄愇偼擇偮偺曈偵懏偟偰偄傞偺偱
丂丂丂丂丂倱亖倎乮倣亅侾乯亖倎倣亅倎 丒丒丒 嘆 丂偑惉傝棫偪傑偡丅
偟偨偑偭偰丄岄愇傪 惓倎妏宍偺堦曈偵増偭偰暲傋懼偊傞偲丄倎楍栚偼偐側傜偢倎屄偺晄懌偑惗偠傞偺偱
丂丂丂丂丂倣亖値亄倎 丒丒丒 嘇 偑惉傝棫偪傑偡丅偙偙偱丄嘇 傪 嘆 偵戙擖偟偰惍棟偡傞偲
丂丂丂丂丂倱亖倎乮値亄倎乯亅倎亖倎値亄倎乮倎亅侾乯丂偡側傢偪丂倱亖倎値亄倎乮倎亅侾乯 丒丒丒 嘊丂偑摼傜傟傑偡丅
丂丂
丂丂
丂

丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂