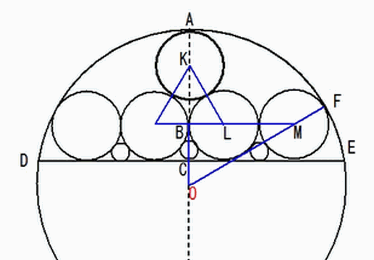
【子神社（ねのじんじゃ）　 明治４２年（１９０９年）】

｛原文｝

 今有如図弧ノ内ニ容等円径五個甲円径五個三個ヲ弦若干得甲円径ヲ間幾何ヲ

 　

 術曰 置百零八個ヲ開平方之ヲ四段テ名天ト置弦ヲ天ヲ以テ除之得甲円径ヲ合問 

｛原文の要訳｝

　計算方法　　　１０８の平方根に９を足した数の平方根を求めて、それに４を掛けた数を天と名づける。

　　　　　　　　　　弦を天で割れば、甲円の直径が求められる。　　　　　　　　　　　

　弦を　ｑ　，甲円の直径を　ｘ　とすると、

　　　　　　　　　　　　　　　　　　　　　　　　　　 ________________

　ｘ＝ｑ　÷　Ｈ　　　である。　ただし　Ｈ＝４√√１０８＋９ とする。

【現代の計算方法】

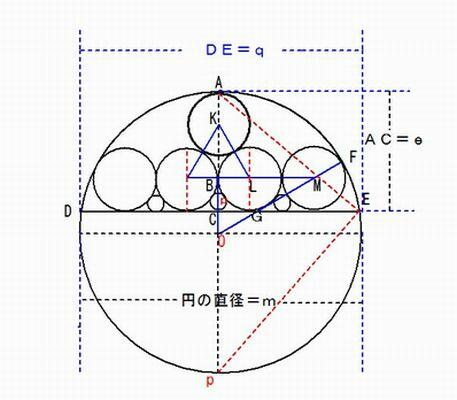
弓形を作る弧の円を　Ｏ（ｍ）、等円を　Ｋ（ｋ）・Ｌ（ｋ）・Ｍ（ｋ）、弦　ＤＥ＝ｑ，矢　ＡＣ＝ｅ，甲円を　Ｐ（ｘ）とする。

  ___

直角三角形　ＫＬＢ 　において、　ＬＢ＝ｋ／２　，ＫＬ＝ｋ　であるから　　ＫＢ＝√３ｋ／２ である。

直角三角形　ＯＢＭ　において、ＯＭ＾２＝ＯＢ＾２＋ＢＭ＾２　　（ＯＦ−ＭＦ）＾２＝（ＯＡ−ＡＫ−ＫＢ）＾２＋ＢＭ＾２

（ｍ／２−ｋ／２）＾２＝（ｍ／２−ｋ／２−√３ｋ／２）＾２＋ （３ｋ／２）＾２

ｍ＾２−２ｋｍ＋ｋ＾２＝ｍ＾２＋ｋ＾２＋３ｋ＾２−２ｋｍ−２√３ｋｍ＋２√３ｋ＾２＋９ｋ＾２

２√３ｋｍ＝１２ｋ＾２＋２√３ｋ＾２　　√３ｍ＝（６＋√３）ｋ　　　ｍ＝（（６＋√３）／√３）ｋ＝（（６√３＋３）／３）ｋ

ｍ＝（２√３＋１）ｋ

ＡＣ：ＣＥ＝ＣＥ：ＣＰ　　　ＣＥ＾２＝ＡＣ×ＣＰ　　　　（ｑ／２）＾２＝ｅ（ｍ−ｅ）

（ｑ／２）＾２＝（ｋ＋√３ｋ／２）（ｍ−ｋ−√３ｋ／２）

ｑ＾２＝（２ｋ＋√３ｋ）（２ｍ−２ｋ−√３ｋ）＝（２ｋ＋√３ｋ）（２（２√３＋１）ｋ）−２ｋ−√３ｋ）＝

（２＋√３）（４√３＋２−２−√３）ｋ＾２＝（６√３＋９）ｋ＾２

  _______________ ______________

ｑ＝√６√３＋９ｋ　　　　　ｋ＝ｑ／（√６√３＋９）

  ____

等円をＬ（ｋ）,甲円を　Ｐ（ｘ）において、　ＣＧ＝√ｋｘ　　　　また　ＣＧ＝ＢＬ＝１ｋ／２

よって　　√ｋｘ＝ｋ／２　　　　　ｘ＝ｋ／４　　　｛■直線上にある等円２円に挟まれた小円の関係の公式■とする｝

　ｘ＝ｑ／（４√６√３＋９）＝ｑ／Ｈ　　　（但し　Ｈ＝４√√１０８＋９　とする）