竜福寺(岩井不動-千葉県旭市)
{原文}
今有如図五角内交画等側円五個容一円只云側円長径一十二寸三分三厘短径図寸一分一厘問容円径幾何
答曰 容円径四寸零九厘有奇術曰置長径以短径除之自之内減一個名初置五個開平方内減一個名中之減初名末自之加
初五段開平方内減末之中二段除之開平方以除短径得容円径合問
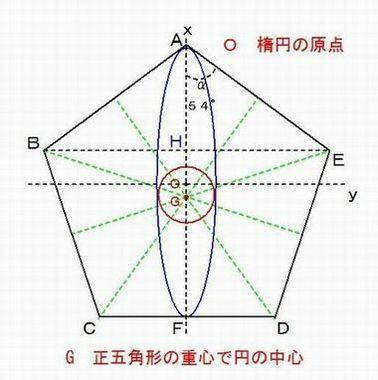
図のように、正五角形の内に等しい楕円を5つ交差して画き、その内に円が接するようにある。
ここで、楕円の長軸を12.33寸、短軸を4.11寸とすると、円の直径は、いくらか
【江戸時代の計算方法】 楕円の長軸を短軸で割った数の2乗から1を引いたものを初と名づける。
5の平方根から1を引いたものを中と名づける。初から中を引いた結果を末と名づける。
末を2乗して初の5倍を足したものの平方根を求め、それから末を引いたものを中の2倍で割り、
それの平方根でで楕円の短軸を割ることにより、円の直径が求められる。
【現代の計算方法】
楕円をO(K=2a,L=2b)とし、Oを原点、長軸をx軸、短軸をy軸とする座標系を設定する。
楕円をOは、x^2/a^+y^2/b^2=1 と表示される。
正五角形の一片AEは楕円Oに接している。
_____________________
∠EAO=αとし m=tanα =tan54° =1/tan36° =1/√(5-2√5)
◆tan(90°-θ)=1/tanθの関係より◆
1/tan54=cos54/sin54 =cos(90-36)/sin(90-36) =sin36/cos36 =tan36
_____________________
y=mx+√m^2a^2 +b^2 ・・・・・証明
楕円 x^2/a^2+y^2/b^2=1 ・・・① p(x1,y1)における接線は
xx1^2/a^2+yy1/b^2=1 y=(b^2x1)x/a^2y1+b^2y1・・・②
この接線の傾きをmとする。 m=-(b^2x1)/a^2y1・・・③
p(x1,y1)は、①上にあるから x1^2/a^2+y1^2/b^2・・・④
③④よりx1を消去すると y1^2=b^4/(m^2a^2+b^2)
∴ y1=±b^2/√(m^2a^2+b^2) 1/y1=±{√(m^2a^2+b^2)}/b^2
∴ b^2/y1=±{√(m^2a^2+b^2)} ②に代入して y=mx±√m^2a^2 +b^2
_______________________________________________________________________________________________________________
点Aの座標は y=0 であるから -mx=√m^2a^2 +b^2
(-mx)^2/m^2=(√m^2a^2 +b^2)^2/m^2 x^2=(m^2a^2+b^2)/m^2
=a^2 +(b^2/m^2)=a^2+b^2/{(1/√(5-2√5) )}^2=a^2 +{(1/√(5-2√5) )}b^2
=a^2+(5-2√5)b^2 a^2 +(5-2√5)b^2=A とする。
____________________________
{-(√a^2 +(5-2√5)b^2 , 0}={-A, 0} A 0=√a^2 +(5-2√5)b^2=√A
_______________________________________ ______________________________________
AF=a+√a^2 +(5-2√5)b^2=a+√a^2 +(5-2√5)b^2=a+√A
正五角形の重心をG,頂点Aから対辺CDに下ろした垂線の足をF、辺AE=CD=J とする。
∠GDF=54℃,∠ADF=72℃ であるから
___________________________________
GF=J×1/2×tan54℃=J×1/2×√(5+2√5)/5
_______________
AF=J×1/2×tan72℃=J×1/2×√5+2√5 したがって
GF:(a+√A)={J(√5+2√5)/(2×√5)} : {J(√5+2√5)/2}
_____________ _____________
GF=(a+√A)√5+2√5/√5(√5+2√5)=a+√A/√5
OG=OF-GF=a-{(a+√A)/√5}={(√5-1)a-√A}/√5
正五角形の重心をG,は、O(x,y) 座標系においては
{((√5-1)a-√a^2+(5-2√5)b^2/√5) , 0} と表示される
客円G,(x=2r)は、正五角形の重心をGを中心とし直系と半径rの楕円Oの内接円である。
右図がGを中心として72℃ずつ1回転すると問題図となる。
楕円の中心Oと内接円の中心Gとの距離をdとすると{公式}により
楕円の長軸 (k=2a) 短軸に2点で内接する円 (m=2r),楕円の中心と内接円の中心との
距離をdとする。
d=(√(k^2-L^2)(L^2-m^2))/2=(√(a^2-b^2)(b^2-r^2))/b
________________________
d=(√(a^2-b^2)(b^2-r^2))/b={(√5-1)a-√a^2 +(5-2√5)b^2 ,}/√5
5(a^2-b^2)(b^2-r^2)=b^2{(√5-1)a-√A}^2
r^2=b^2-b^2{(√5-1)a-√A}^2/5(a^2-b^2)=
b^2[5a^2-5b^2-{(√5-1)a-√A}^2]/5(a^2-b^2)=(b^2-B)/ 5(a^2-b^2)
B= 5a^2-5b^2-6a^2+2√5a^2+2(√5-1)a√A-a^2-(5-2√5)b^2
√5-1=G とする
= 5a^2-5b^2-6a^2+2√5a+2Ga√A-a^2-5b^2+2√5b^2
= 2√5a-2a^2-10b^2+2√5b^2+2Ga√A=2{(√5-1)a^2-√5(√5-1)b^2Ga√A}
________________________
= 2G(a^2-√5b^2+a√A)=2Gb^2{a^2-√5b^2+a√a^2 +(5-2√5)b^2}/5(a^2-b^2)
x^2/4=分子/5{(k^2/4)-(L^2/4)}
分子=2G(L^2/4){(k^2/4)-(√5L^2/4)+2/k√(k^2/4)+(5-2√5)L^2/4}
=([2GL^2{(k^2-√5L^2+k√k^2+(5-2√5)L^2}]/(4×4))/{5(k^2-L^2)}/4
x^2=[2GL^2{(k^2-√5L^2+k√k^2+(5-2√5)L^2}]/5(k^2-L^2)=2GLC/5(k^2-L^2)
分母・分子に D=k√k^2+5(5-2√5)L^2-(k^2-√5L^2) を掛けて
x^2=(2GL^2CD)/{5(k^2-L^2)}D
CD={k,√k^2+5(5-2√5)L^2}-(k^2-√5L^2)^2=
{k^2+(5-2√5)kL^2}-k^4+2√5k^2L-5L^4=5k^2L-5L^4=5L^2(k^2-L^2)
x^2={2GL^5L^2(k^2-L^2)}/{5(k^2-L^2)}×D=2GLL^2/D
D=k√k^2+5(5-2√5)L^2-(k^2-√5L^2)=√k^4+(5-2√5)k^2L^2-(k-√5L^2)=
{√k^4-2√5k^2L^2+5L^4+5k^2L^2-5L^4}-(k^2-L^2)=2GLL^2/D=
(2GLL^2÷L^2)/(D÷L^2)=2GL^2/(D÷L^2)
D/L^2=√{(k^2-√5L^2)^2/L^4}+{5L^2(k^2-L^2)/L^4}-{(k^2-√5L^2)/L^2}
(K/L)^2-1=H (K/L)^2-√5=P=√P^2+5H-P
x^2=2GL^2/(√P^2+5H-P)=L^2/{(√P^2+5H-P)÷2G}
x=L/{(√P^2+5H-P)÷2G}=L÷{(√P^2+5H-P)÷2G}=
411/√2.49677÷2.47212=4.11/1.00997=4.06974
k=12.33 L=4.11 のとき
H=(12.33÷4.11)^2-1=8
G=2.23606-1=1.23606
P=9-2.23606=6.76394
√P^2+5H-P=√45.75088+40-6.76394=9.26017-6.76394=2.49677