不動堂(茨城県土浦市)
{原文}
今有如図円擣斜乃之截容甲球二個「乃甲球二個者如径」乙球一個只云甲球径若干問得乙球径径術如何
答曰 如左術 術曰置四千一百三十一個開平方以減一百四十四個余乗甲球径以八十一除之得乙球径合問
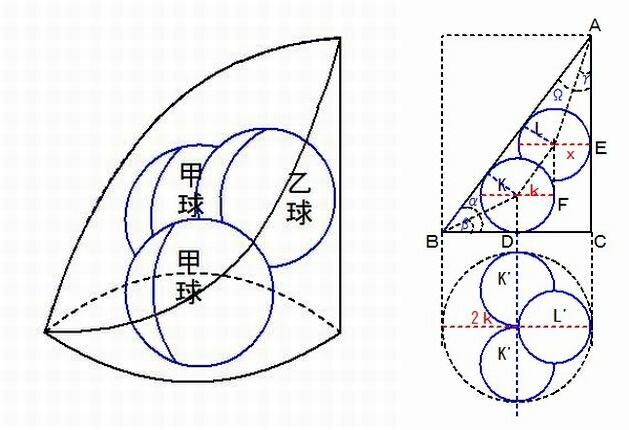
図のように、円柱を斜めに載ったものの内に、甲球2つ「甲球2つの直径の和は、円柱の直径に等しい」と乙球1つとが接するようにある。
ここで、甲球の直径を用いて、乙球の直径を求める方法はどのようであるか。
【江戸時代の計算方法】 4131を平方に開いて144から引き、それに甲球の直径を掛けた結果を81で割れば
乙球の直径が求めらる。 甲球の直径をk、乙球の直径をxとすると
x=(144-√4131)k÷81 である。
【現代の計算方法】 甲球をK(k),円柱の直径BC=2k、乙球をL(x),∠ABC=α、∠KBD=β とする。
tanβ=KD/BD=1/2 である。 α=2β であるから、 tanα=tan2β=tan(β+β)
____________________________________________________________
◆tanの加法定理の証明◆
tan(α+β)=sin(α+β)/cos(α+β)=(sinαcosβ+cosαsinβ)/(cosαcosβ-sinαsinβ)
tanを作る為にcosαcosβで割る。 分子: (sinαcosβ)/(cosαcosβ)+(cosαsinβ)/(cosαcosβ)=
(sinα/cosα)+(sinβ/cosβ)=tanα+tanβ
分母: (cosαcosβ)/(cosαcosβ)-(sinαsinβ)/(cosαcosβ)=1-(sinαsinβ)/(cosαcosβ)=
1-tanα+tanβ 分子/分母=(tanα+tanβ)/(1-tanα+tanβ)
____________________________________________________________
tanα=(2×tanβ)/(1-tanβ^2)={2×(1/2)}/{1-(1/2)^2}=1/{1-(1/4)}=4/3
したがって、 AC=BCtanα=2k(4/3)=(8k)/3
◆三角関数sec, cosec, cotと記号の意味◆
sec(x)=1/cos(x) cosec(x)=1/sin(x) cot(x)=1/tan(x)
sec のことを正割(セカント),cosec のことを余割(コセカント),cot のことを余接(コタンジェント)と呼びます。
________________________________________________
∠LAE=γ(ガンマ) とすると (α+Ω)+90=180 α=2β Ω(オメガ)=2γ
(2β+2γ)=90 2(β+γ)=90 β+γ=45 cot45=1/tan45=cot(β+γ)
cot (β+γ) = {(cot β cotγ ) − 1}/ (cot β + cot γ) 直角三角形なので tan45=1
1={(cotβcotγ)-1}/(cotβ+cotγ) 1={(cotβcotγ)-1}/(cotβ+cotγ)
cotβ=2 であるから 1=(2cotγ-1)/(2+cotγ) cotγ+2=2cotγ-1
2cotγ-3=cotγ (2cotγ- cotγ)-3=cotγ- 3 cotγ=3
cotγ=x/2 cotγ=3x/2 直角三角形LKFにおいて LK^2=KF^2+LF^2
1/4(x^2+2kx)=(k-x/2)^2+(8k/3-3x/2-1k/2)
(x^2+2kx)/4={(2k-x)^2}/4+{(13k-9x^2}/36
9x^2+18kx=36k^2-36kx+9x^2+169k^2-234kx+81x^2
81x^2-288kx+205k^2=0 x=(144±√144^2-81×205)k/81=
(144-√20736-16605)k/81=(144-√4131)k/81


